The First Derivative Test

Sun Surfer Math
25 Sept 202211:44
EducationalLearning
32 Likes 10 Comments

TLDRThe video script introduces the first derivative test, a method for determining the nature of critical points on a function's graph. It begins with a graphical representation where the derivative's sign indicates the slope of the tangent line: positive for increasing sections and negative for decreasing ones. The script explains that a critical point, where the first derivative equals zero, can be either a relative maximum or minimum. To apply the first derivative test, one must evaluate the sign of the derivative to the left and right of the critical point. If the derivative changes from positive to negative, the point is a relative maximum; if it changes from negative to positive, it's a relative minimum. The script illustrates this with two examples, first with a simple quadratic function and then with a more complex cubic function, demonstrating how to find critical points and classify them using the first derivative test.

Takeaways
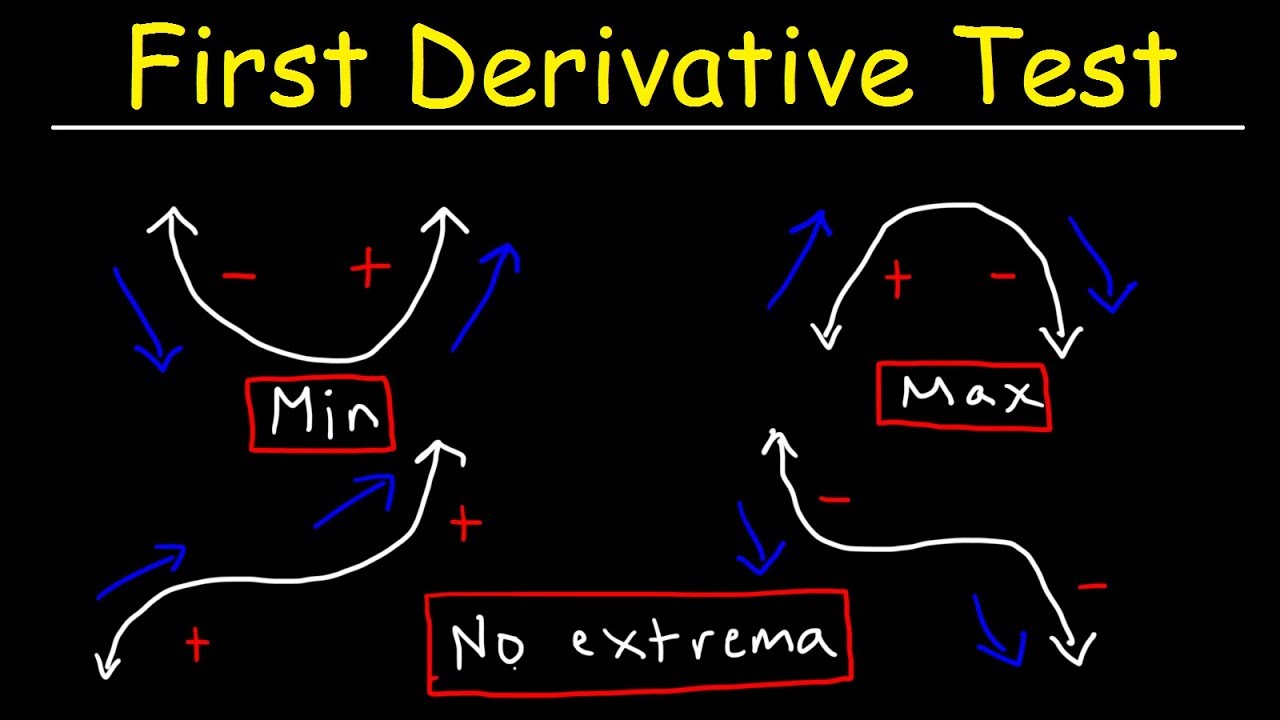
  • 📈 The first derivative test is used to determine if a critical point is a relative maximum or minimum.
  • 🔍 A critical point occurs where the first derivative (F'(x)) is equal to zero.
  • 🔺 If the derivative is positive to the left of a critical point and negative to the right, it's a relative maximum.
  • 🔻 Conversely, if the derivative is negative to the left and positive to the right, the point is a relative minimum.
  • ↗️ A positive derivative signifies an increasing slope, indicating an upward trend in the function's graph.
  • ↘️ A negative derivative indicates a decreasing slope, showing a downward trend in the graph.
  • 📐 The slope of a tangent line at any point on the graph represents the value of the derivative at that point.
  • 🧮 To apply the first derivative test, evaluate the sign of the derivative at points on either side of the critical point.
  • 📌 A horizontal tangent line corresponds to a slope of zero, which is a characteristic of critical points.
  • 🌐 The overall trend of the function's graph between critical points dictates the sign of the derivative in those intervals.
  • 📝 For example, in the function f(x) = 8 + 2x - x^2, the critical point at x = 1 is a relative maximum as the derivative changes from positive to negative.
  • 🔑 The first derivative test is a valuable tool for analyzing the behavior of functions and their critical points without graphing.
Q & A

  • What is the first derivative test used for in calculus?

    -The first derivative test is used to determine whether a critical point on a function is a relative maximum, relative minimum, or neither.

  • What does it mean if the derivative of a function is positive between two points A and B?

    -If the derivative is positive between A and B, it indicates that the function is increasing from left to right, and the tangent lines have a positive slope in that interval.

  • What is the slope of a horizontal tangent line?

    -The slope of a horizontal tangent line is zero because it is parallel to the x-axis.

  • What is a critical point in calculus?

    -A critical point is a point on the graph of a function where the derivative is either zero or undefined.

  • How can you determine if a critical point is a relative maximum or minimum using the first derivative test?

    -If the derivative changes from positive to negative as you move from left to right through the critical point, it is a relative maximum. If the derivative changes from negative to positive, it is a relative minimum.

  • What is the derivative of the function f(x) = 8 + 2x - x^2?

    -The derivative of the function is f'(x) = 2 - 2x.

  • At what value of x does the derivative of the function f(x) = 8 + 2x - x^2 equal zero?

    -The derivative equals zero when x = 1.

  • What is the first derivative of the function f(x) = 13x^3 + (3/2)x^2 - 10x + 12?

    -The first derivative is f'(x) = 39x^2 + 3x - 10.

  • What are the critical points for the function f(x) = 13x^3 + (3/2)x^2 - 10x + 12?

    -The critical points are x = -5 and x = 2.

  • How can you determine if a critical point is increasing or decreasing without graphing the function?

    -By evaluating the sign of the first derivative at points to the left and right of the critical point. If the derivative is positive to the left and negative to the right, the point is a relative maximum. If the derivative is negative to the left and positive to the right, the point is a relative minimum.

  • What is the conclusion about the critical points for the function f(x) = 13x^3 + (3/2)x^2 - 10x + 12?

    -The conclusion is that x = -5 is a relative maximum and x = 2 is a relative minimum.

  • Why is it important to test points to the left and right of a critical point when using the first derivative test?

    -Testing points to the left and right of a critical point allows you to observe the change in the sign of the derivative, which is crucial for determining whether the critical point is a relative maximum or minimum.

Outlines
00:00
📈 Introduction to the First Derivative Test

The video begins with an introduction to the first derivative test, a method used to analyze the behavior of a function's graph. The presenter uses a graph to explain how the derivative, which represents the slope of the tangent line, can be positive or negative depending on whether the graph is increasing or decreasing. The concept of a critical point, where the derivative equals zero, is introduced. The video then explains how to determine if a critical point is a relative maximum or minimum by examining the sign of the derivative to the left and right of the point.

05:00
🔍 Applying the First Derivative Test with a Simple Function

The presenter demonstrates the first derivative test using a simple function, f(x) = 8 + 2x - x^2. The derivative, f'(x) = 2 - 2x, is found and set to zero to locate the critical point at x = 1. To determine if this is a relative maximum or minimum, the derivative is evaluated at points to the left (x = 0) and right (x = 2) of the critical point. The sign of the derivative indicates whether the function is increasing or decreasing, thus revealing the nature of the critical point as a maximum.

10:02
🔢 Using the First Derivative Test with a More Complex Function

The video continues with a more complex function, f(x) = 13x^3 + (3/2)x^2 - 10x + 12, to find and classify its critical points. The derivative, f'(x) = 39x^2 + 3x - 10, is set to zero and factored to find the critical points at x = -5 and x = 2. The first derivative test is applied by evaluating the derivative at points around the critical points (x = -6, x = 0, and x = 3). The change in sign of the derivative from positive to negative indicates a relative maximum at x = -5, and from negative to positive indicates a relative minimum at x = 2.

Mindmap
Keywords
💡First Derivative Test
The First Derivative Test is a mathematical method used to determine whether a given critical point on a function is a relative maximum or minimum. In the video, it is introduced as the primary tool to analyze the behavior of a function's slope around critical points. The test involves evaluating the sign of the first derivative to the left and right of the critical point. If the derivative changes from positive to negative, the point is a relative maximum; if it changes from negative to positive, the point is a relative minimum.
💡Derivative
In calculus, the derivative of a function represents the rate at which the function is changing at a certain point. It is the slope of the tangent line to the function's graph at that point. In the context of the video, the derivative is used to analyze the increasing or decreasing nature of a function's graph, which is crucial for applying the First Derivative Test.
💡Critical Point
A critical point on a function is a point where the derivative is either zero or undefined. These points are of interest because they are potential locations for relative maxima or minima. In the video, finding critical points is the first step before applying the First Derivative Test to determine the nature of these points.
💡Tangent Line
A tangent line to a curve at a given point is a straight line that 'just touches' the curve at that point. The slope of this line is equal to the derivative of the function at that point. In the video, the concept of the tangent line is used to visualize the slope of the function and to understand how the slope changes as we move along the curve.
💡Positive Slope
A positive slope indicates that as we move from left to right along a curve, the curve is increasing. In the video, a positive slope of the tangent line is associated with the function being in an increasing phase, which is a key observation when applying the First Derivative Test.
💡Negative Slope
A negative slope means that the curve is decreasing as we move from left to right. In the context of the video, a negative slope is important for identifying regions where the function is decreasing, which helps in determining if a critical point is a relative minimum.
💡Relative Maximum
A relative maximum is a point on a function where the function reaches a peak that is higher than the surrounding points, though not necessarily the highest peak on the entire function. In the video, the First Derivative Test is used to identify such points by looking for a sign change from positive to negative in the derivative around the critical point.
💡Relative Minimum
A relative minimum is a point where the function dips to a low that is lower than the surrounding points, but not necessarily the lowest point on the entire function. The video explains that a relative minimum can be found by observing a sign change from negative to positive in the derivative around a critical point.
💡Function
In mathematics, a function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. The video focuses on analyzing the behavior of specific functions using the First Derivative Test to find and classify their critical points.
💡Slope
The slope of a line is a measure of its steepness, or how much it rises or falls vertically for a given horizontal distance. In the video, the concept of slope is central to understanding the derivative, as the derivative at any point on a function is the slope of the tangent line at that point.
💡Graph
A graph is a visual representation of a function, showing how the dependent variable (usually the y-values) relates to the independent variable (usually the x-values). The video uses graphs to illustrate the concept of derivatives and to visually show how the First Derivative Test can be applied to identify critical points and their nature.
Highlights

Introduction to the first derivative test for determining relative maxima and minima.

Explanation of the derivative as the slope of a tangent line to a graph.

Positive derivative between points A and B indicates an increasing graph from left to right.

At point B, the derivative is zero, which is a critical point.

Negative derivative between points B and C signifies a decreasing graph from left to right.

Second critical point identified at point C with a horizontal tangent line.

Positive derivative between points C and D indicates increasing tangent lines.

The first derivative test uses changes in the sign of the derivative to identify maxima and minima.

A critical point is a maximum if the derivative changes from positive to negative.

A critical point is a minimum if the derivative changes from negative to positive.

Example provided with the function f(x) = 8 + 2x - x^2 to illustrate the first derivative test.

Derivative f'(x) = 2 - 2x is found and set to zero to find critical points.

Critical point at x = 1 is identified and evaluated for increasing and decreasing slopes.

The point x = 1 is determined to be a relative maximum using the first derivative test.

Second example with the function f(x) = 13x^3 + (3/2)x^2 - 10x + 12 is used to demonstrate the test.

Derivative f'(x) = 39x^2 + 3x - 10 is found and set to zero to find critical points.

Two critical points, x = -5 and x = 2, are identified.

Using the first derivative test, x = -5 is determined to be a relative maximum and x = 2 a relative minimum.

Transcripts

Browse More Related Video

First Derivative Test

Second derivative test | Using derivatives to analyze functions | AP Calculus AB | Khan Academy

Concavity and the 2nd Derivative Test

3.2 - Using Second Derivatives to Classify Max and Min Values

Concavity introduction | Using derivatives to analyze functions | AP Calculus AB | Khan Academy

3.1 - Using First Derivatives to Classify Max and Min Values

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Derivative TestCalculusMaxima MinimaCritical PointsMath EducationGraph AnalysisSlope InterpretationTangent LinesFunction AnalysisEducational ContentMath Tutorial