Draw the Function given Graph of Derivative
TLDRThis educational video script explains the process of reconstructing a function from its derivative graph. It highlights that the original function's maxima and minima correspond to the derivative's zeros, and the function's increasing or decreasing nature is mirrored by the derivative's position relative to the x-axis. The script also clarifies that the slope of the original function at any point is equivalent to the y-value of the derivative at that point. It uses examples to illustrate how to interpret the derivative graph to infer the behavior of the original function, including identifying points of inflection and applying these principles to specific cases like cubic and trigonometric functions.
Takeaways
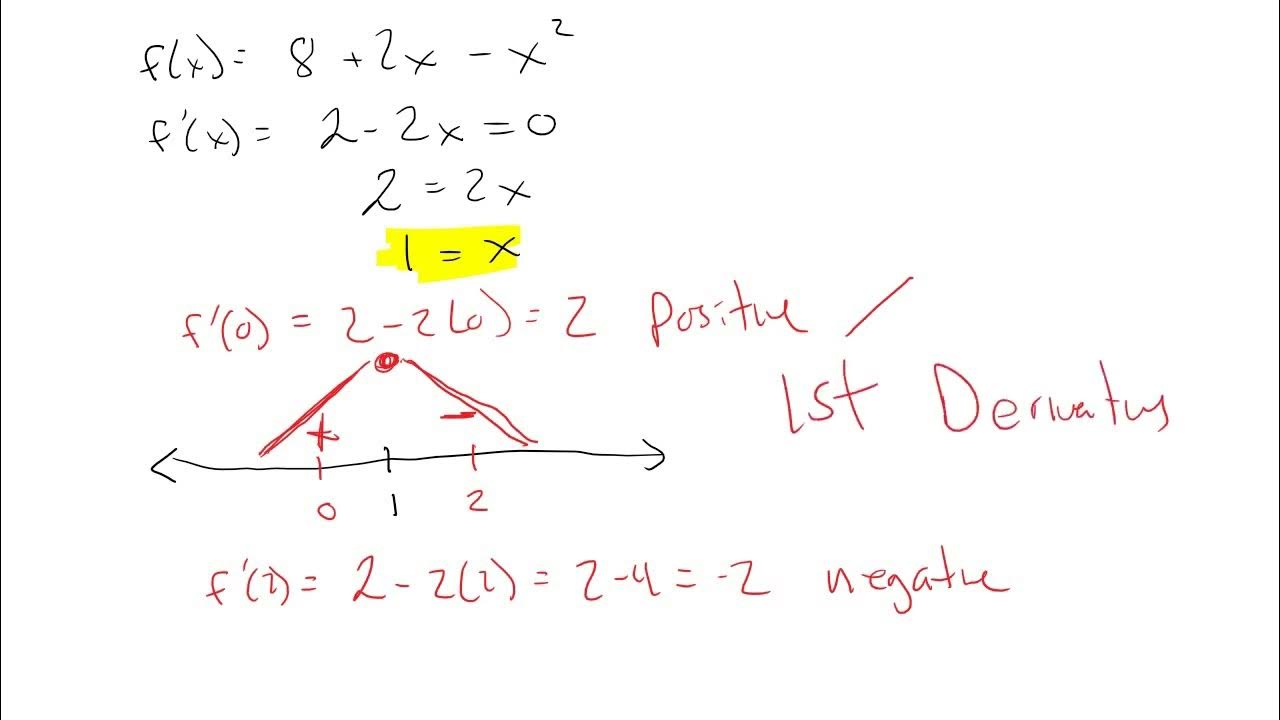
- 📌 The derivative of a function at a point is zero if the original function has a maximum or minimum there.
- 📈 If the derivative is negative, the original function is decreasing; if positive, the original function is increasing.
- 🔄 X-intercepts on the graph of the derivative correspond to maximums or minimums (or points of inflection) on the original function.
- 🤔 A point of inflection is a special case where the slope is zero, but the function continues to decrease on both sides without switching from decreasing to increasing.
- ↗️ Flipping from a negative to a positive derivative indicates a minimum in the original function.
- ↙️ Conversely, flipping from a positive to a negative derivative indicates a maximum.
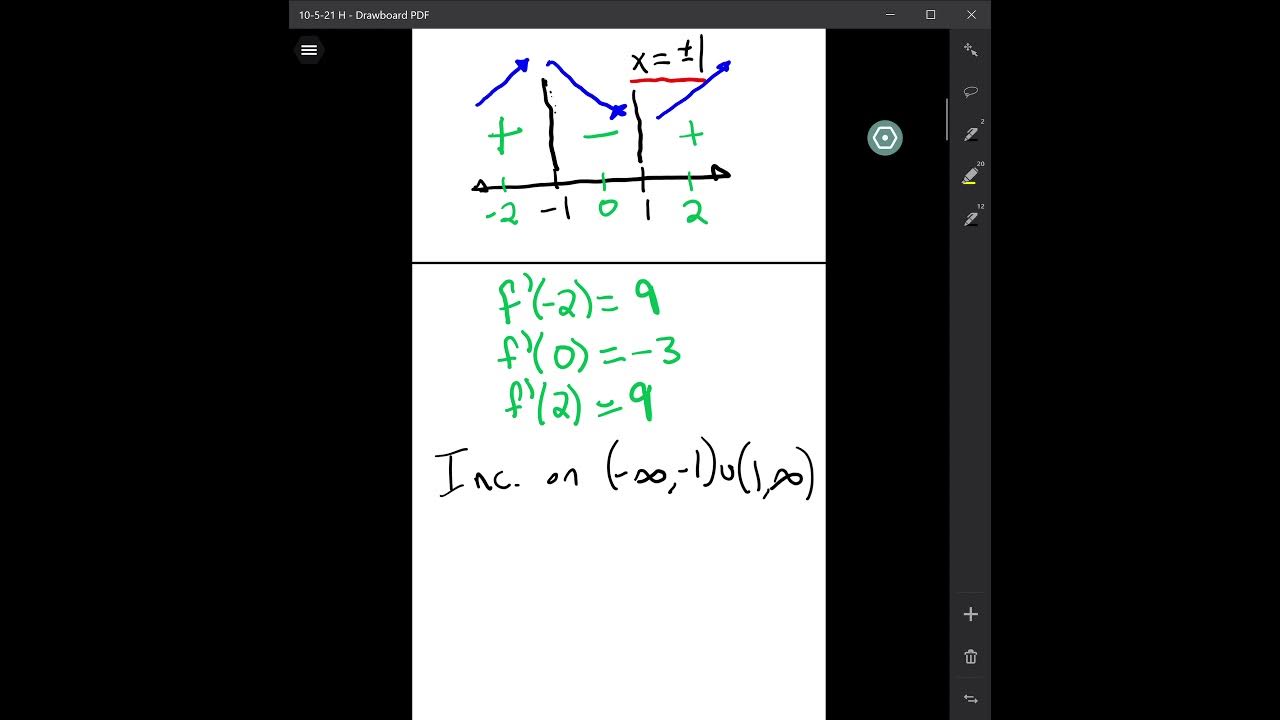
- 📈 An increasing function (above the x-axis in the derivative) implies an increasing original function.
- 📉 A decreasing function (below the x-axis in the derivative) implies a decreasing original function.
- 🔄 The slope of the original function at any point can be estimated by the y-value of the derivative at that point.
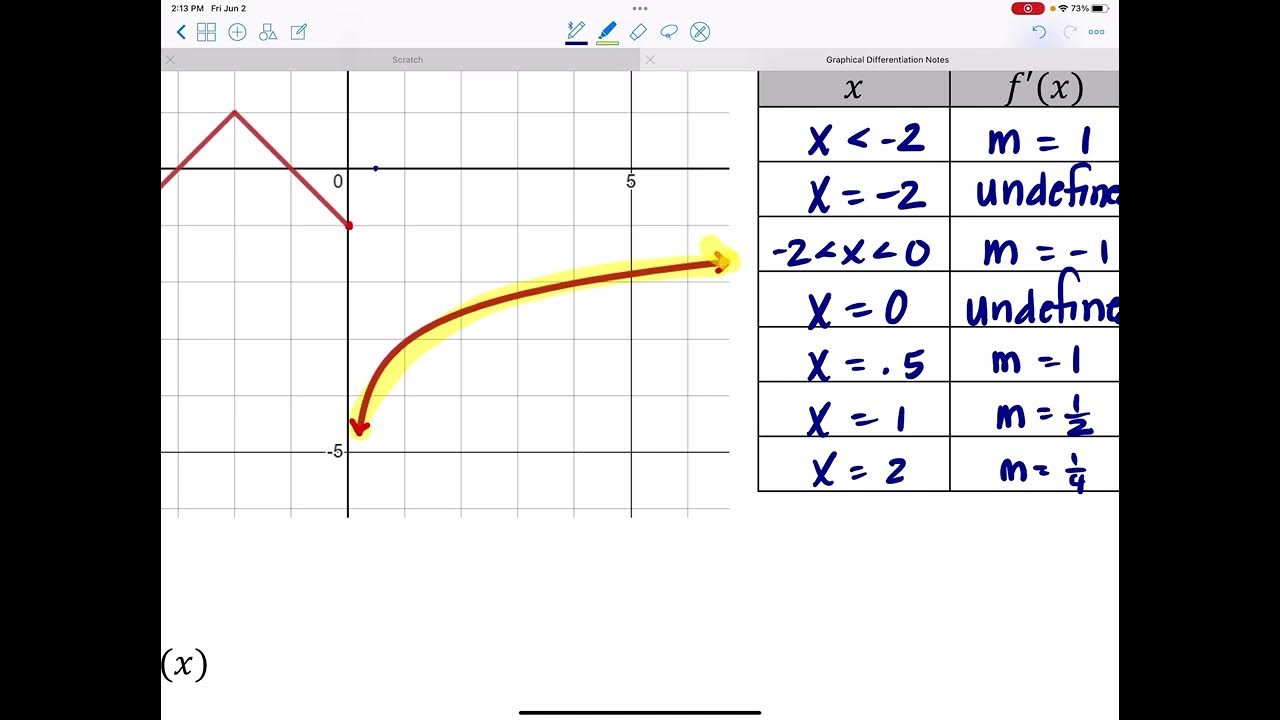
- 📊 Given points on a grid, the y-value of the derivative at those points represents the slope of the original function.
- 🧮 The derivative of a cubic function is a quadratic, which can help in understanding the shape of the original function from its derivative.
- ⚖️ The rules of derivatives apply universally, regardless of the specific function, including those for trigonometric functions like cos(x).
Q & A
What is the relationship between the original function and its derivative?
-The derivative of a function represents the rate of change or the slope of the original function. If the original function reaches a maximum or minimum, its derivative is zero at those points.
How do X intercepts on the graph of the derivative relate to the original function?
-X intercepts on the graph of the derivative correspond to maximums, minimums, or points of inflection on the original function.
What does it mean if the derivative is negative?
-A negative derivative indicates that the original function is decreasing.
What does it mean if the derivative is positive?
-A positive derivative indicates that the original function is increasing.
How can the slope of the original function be determined from the derivative?
-The Y value of the derivative at any point represents the slope of the original function at that point.
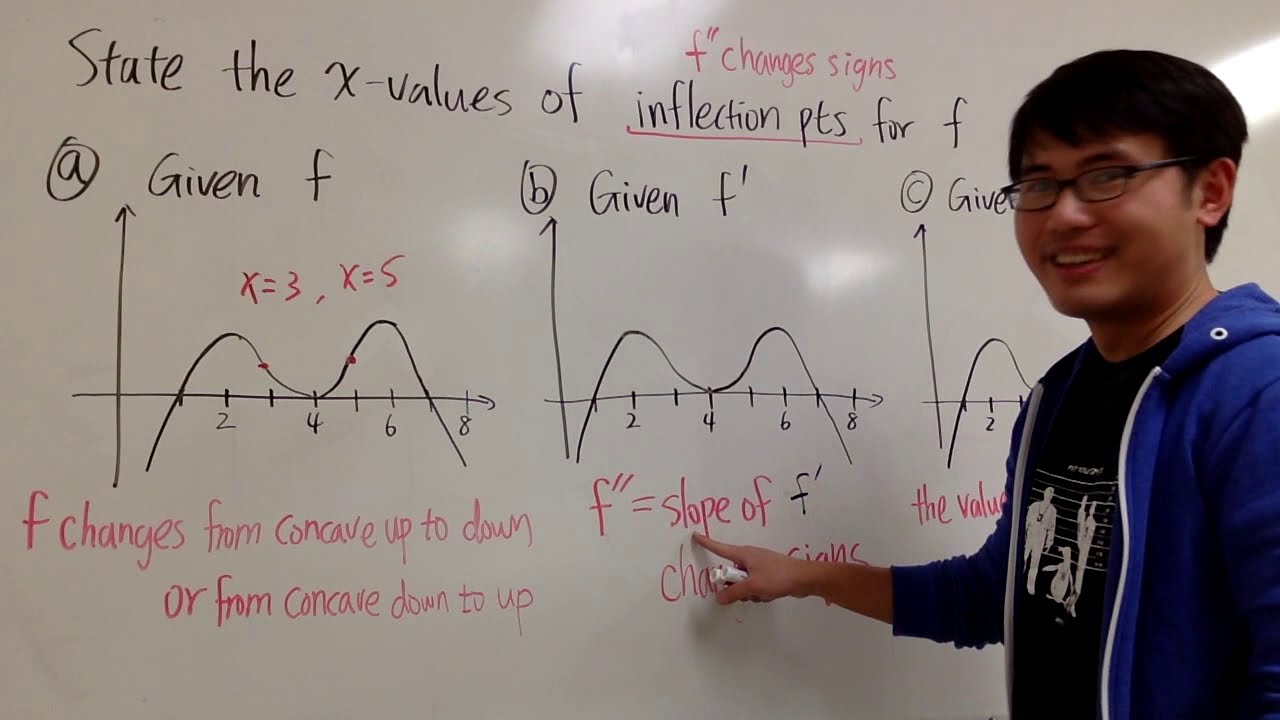
What is a point of inflection and how does it appear on the derivative graph?
-A point of inflection is a point on the original function where the concavity changes. On the derivative graph, it appears as a point where the slope is zero but does not switch from decreasing to increasing or vice versa.
How can you determine whether a point on the original function is a maximum or a minimum based on the derivative?
-A point on the original function is a maximum or minimum if the derivative changes sign around that point, indicating a change from increasing to decreasing or decreasing to increasing.
What is the significance of the derivative being above or below the x-axis on the original function's behavior?
-If the derivative is above the x-axis, the original function is increasing; if it is below the x-axis, the original function is decreasing.
Why is it important to know the derivative of a cubic function?
-Knowing that the derivative of a cubic function is a quadratic is useful because it helps in understanding the behavior of the original function, such as its increasing and decreasing intervals.
How does the derivative of trigonometric functions like cos(x) relate to the original function?
-The derivative of cos(x) is -sin(x), which means the original function, when it is a trigonometric function like cos(x), will have its rate of change represented by -sin(x).
What is the practical advice given in the script for practicing drawing the original function from its derivative?
-The script advises practicing by applying the rules discussed, such as the relationship between X intercepts, maximums, minimums, and points of inflection, and to ask questions for further clarification.
Outlines
📚 Understanding Derivatives to Sketch Original Functions
This paragraph explains the process of drawing the original function from its derivative graph. It emphasizes that the derivative being zero indicates a maximum or minimum in the original function, and the sign of the derivative (negative for decreasing, positive for increasing) reflects the behavior of the original function. The paragraph also discusses the concept of a point of inflection, where the function changes from decreasing to increasing without a maximum or minimum, and how the slope of the original function directly gives the Y value of the derivative. An example is used to illustrate these concepts, including the transformation of X intercepts and the importance of the slope in determining the function's behavior.
📈 Applying Derivative Rules to Sketch Functions: Examples and Insights
The second paragraph delves deeper into the application of derivative rules to sketch original functions, using specific examples. It covers how to interpret the derivative's behavior to infer the original function's increasing or decreasing nature and the significance of X intercepts in determining maximums, minimums, or points of inflection. The paragraph provides a step-by-step guide on sketching the original function from its derivative, including handling quadratic functions derived from cubic originals and verifying the process with trigonometric functions. It encourages practice and offers help for any questions, concluding with a reminder to enjoy life and prepare for tests.
Mindmap
Keywords
💡Derivative
💡Original Function
💡Maximum and Minimum
💡X-intercepts
💡Increasing and Decreasing
💡Slope
💡Point of Inflection
💡Cubic and Quadratic Functions
💡Trigonometric Functions
💡Practice
Highlights
Deriving the original function from its derivative is an exact reverse process.
Wherever the derivative is zero, the original function has a maximum or minimum at that point.
X-intercepts on the graph of the derivative correspond to maxima or minima on the original function.
A negative derivative indicates the original function is decreasing, while a positive derivative indicates it is increasing.
Estimating the slope on the original function directly gives you the Y value of the derivative.
Points of inflection occur where the derivative is zero but does not change from decreasing to increasing.
An X-intercept on the derivative graph that switches from negative to positive indicates a minimum on the original function.
If the derivative is above the X-axis, the original function is increasing.
X-intercepts on the derivative graph can also represent points of inflection, not just maxima or minima.
A point of inflection is characterized by a slope that remains zero but does not switch the direction of the function's increase or decrease.
The derivative of a cubic function is a quadratic function.
An X-intercept on the derivative that switches from increasing to decreasing indicates a maximum on the original function.
The derivative of cos(x) is -sin(x), verifying the rules for deriving the original function from its derivative.
Practicing deriving the original function from its derivative is encouraged for better understanding.
Understanding the relationship between the derivative and the original function is crucial for solving calculus problems.
The process of deriving the original function from its derivative involves recognizing changes in slope and direction.
The derivative graph's X-intercepts, slope changes, and points of inflection are key to reconstructing the original function.
The video provides a comprehensive guide on how to draw the original function from its derivative graph.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: