Tensor Calculus Lecture 10b: The Normal Derivative
TLDRThis lecture delves into the concept of normal derivatives, crucial for understanding the divergence theorem and Gauss's theorem. It explains the invariant definition of a normal derivative on a surface in Euclidean space, how to measure the rate of change of a function in the normal direction to the surface, and the relationship between the normal derivative and the covariant derivative. The lecture also explores the second normal derivative and its expression in terms of the covariant derivative and surface characteristics. It concludes with a discussion on the connection between the ambient Laplacian and the surface Laplacian, showcasing the application of various elements of tensor calculus.
Takeaways
- 📚 The lecture focuses on the concept of normal derivatives, which are crucial for understanding Gauss's theorem and their applications in integration.
- 🔍 The normal derivative is defined as the rate of change of a function in the direction normal to a surface, highlighting its physical and geometric significance.
- 📏 An invariant definition of the normal derivative is discussed, which involves drawing a straight line through a point in the normal direction to the surface and measuring the rate of change along this line.
- 📈 The lecturer introduces a Cartesian coordinate system in the Euclidean space to simplify the derivation process, although it's noted that this is a 'wrong' but quicker approach.
- 🔗 The connection between the function defined on the surface and the ambient space is established by parameterizing a straight line and expressing the function in terms of the ambient coordinates.
- 📉 The normal derivative is expressed as the dot product of the gradient of the function and the unit normal vector to the surface, leveraging the properties of Euclidean space.
- 🔑 The second normal derivative is explored, which involves evaluating the second derivative of the function along the normal direction, and its relationship with the curvature of the surface.
- 🌐 The lecturer contemplates the implications of defining normal derivatives in non-Euclidean spaces, suggesting the use of geodesics instead of straight lines.
- 🔄 The process of deriving the relationship between the ambient Laplacian of a function and its surface Laplacian is outlined, incorporating various elements of tensor calculus.
- 🔍 The final expression for the relationship between the ambient and surface Laplacian is presented, demonstrating the application of the chain rule, curvature tensor, and covariant derivatives.
- 🎓 The lecture emphasizes the importance of mastering tensor calculus for understanding complex concepts in differential geometry and their practical applications.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the normal derivative, its definition, and its applications, particularly in relation to the divergence theorem and Gauss's theorem.
Why did the lecturer decide to cover the topic of normal derivatives?
-The lecturer decided to cover normal derivatives because it is an important topic with significant applications in integration and because it was realized as an oversight in the lecture series.
What is the invariant definition of the normal derivative?
-The invariant definition of the normal derivative involves measuring the rate of change of a function in the direction normal to a surface at a given point in a three-dimensional Euclidean space.
How is the normal derivative related to the divergence theorem?
-The normal derivative is related to the divergence theorem because the theorem has the normal derivative on the right-hand side, making it an essential concept for understanding the theorem.
What is the physical and geometric significance of the normal derivative?
-The physical and geometric significance of the normal derivative is that it captures the rate of change of a function in the direction perpendicular to a surface, which is crucial for understanding how a function behaves in the immediate vicinity of the surface.
How is the normal derivative defined more precisely in the context of a surface in a Euclidean space?
-More precisely, the normal derivative is defined by drawing a straight line through a given point in the direction normal to the tangent space of the surface and measuring the rate of change of the function along this line.
What role does the ambient space play in defining the normal derivative?
-The ambient space, which is assumed to be Euclidean in this context, provides the framework for defining the normal direction and the straight line along which the normal derivative is measured.
Why is the Cartesian coordinate system used in the lecture?
-The Cartesian coordinate system is used in the lecture for simplicity and to quickly arrive at the answer. It allows for a straightforward parameterization of the straight line used to define the normal derivative.
What is the relationship between the normal derivative and the covariant derivative?
-The normal derivative can be expressed in terms of the covariant derivative of a function in the ambient space and some differential characteristics of the surface, such as the normal vector to the surface.
How does the lecturer approach the derivation of the normal derivative in a non-Euclidean space?
-The lecturer suggests that in a non-Euclidean space, one might have to use a geodesic instead of a straight line to define the normal derivative, but the exact approach is left for future exploration.
What is the significance of the second normal derivative in the lecture?
-The second normal derivative is significant as it extends the concept of the normal derivative to second-order changes, which is important for understanding the curvature and behavior of functions on surfaces.
How does the lecturer connect the ambient Laplacian to the surface Laplacian?
-The lecturer connects the ambient Laplacian to the surface Laplacian by using tensor calculus, the chain rule, the derivative of the metric tensor, and the projection formula, showing that the surface Laplacian can be expressed as a sum of terms involving the ambient Laplacian and additional terms related to the curvature of the surface.
Outlines
📚 Introduction to Normal Derivatives
This paragraph introduces the concept of normal derivatives, which the lecturer realized was omitted from previous lectures. It is highlighted as an essential topic with significant applications in integration and the divergence theorem. The lecturer sets the stage for the derivation of Gauss's theorem in the next lecture, emphasizing the importance of understanding normal derivatives in both a physical and geometric context. The paragraph concludes with a preliminary definition of the normal derivative in the context of a three-dimensional Euclidean space.
📐 Formalizing the Normal Derivative
The lecturer delves into a more precise definition of the normal derivative, explaining how it is measured along a straight line normal to the surface at a given point. The importance of the Euclidean nature of the ambient space is discussed, and the lecturer invites the audience to consider how the definition might change in a non-Euclidean space. The paragraph concludes with a parameterization of the straight line and an exploration of how the normal derivative relates to the function defined on the surface and in the ambient space.
🔍 Deriving the Normal Derivative in Cartesian Coordinates
The lecturer chooses Cartesian coordinates for simplicity and expedience, despite acknowledging it as a 'wrong' approach in the spirit of tensor calculus. A detailed parameterization of the straight line in Cartesian coordinates is provided, and the connection between the function defined on the surface and in the ambient space is established. The paragraph culminates in the derivation of the normal derivative as the dot product of the unit normal vector and the gradient of the function.
🔄 Exploring the Second Normal Derivative
Building on the previous discussion, the lecturer explores the second normal derivative, cautioning against common mistakes in differentiation. The process involves evaluating the second derivative of the function with respect to the parameter s, and the lecturer emphasizes the importance of doing so at the correct point. The paragraph concludes with an expression for the second normal derivative that includes the second-order covariant derivative and the properties of the ambient space.
🌐 Reflecting on Non-Euclidean Spaces
The lecturer contemplates the implications of defining normal derivatives on non-Euclidean spaces, suggesting that geodesics might replace straight lines in such contexts. There is a brief discussion on how the definition of the second normal derivative might be affected, hinting at the need for a more general approach that does not rely on the specific properties of Cartesian or Euclidean spaces.
🔗 Connecting Ambient and Surface Laplacians
The relationship between the ambient Laplacian of a function defined in the entire space and its surface Laplacian is examined. The lecturer uses a comprehensive approach that involves the chain rule, the derivative of the metric tensor, the mean curvature, and the projection formula. The paragraph showcases the application of various elements of differential geometry, culminating in an expression that relates the surface Laplacian to the ambient Laplacian.
📘 Rectifying the Path to Tensor Calculus
The lecturer reflects on the derivation process, acknowledging the expedience of using Cartesian coordinates but recognizing the need for a more general and coordinate-invariant approach. The paragraph discusses the importance of tensor calculus and its coordinate invariance, hinting at a future correction of the approach to align with the principles of tensor calculus.
📝 Final Thoughts and Closing Remarks
In the final paragraph, the lecturer summarizes the key takeaways from the lecture, emphasizing the importance of the calculations performed and the elements of differential geometry involved. The paragraph concludes with a note of personal urgency, as the lecturer must leave, but not before expressing gratitude to the audience for their attention and promising to continue the discussion in a future lecture.
Mindmap
Keywords
💡Normal Derivative
💡Divergence Theorem
💡Gauss's Theorem
💡Euclidean Space
💡Parametrization
💡Covariant Derivative
💡Christoffel Symbols
💡Mean Curvature
💡Tensor Calculus
💡Laplacian
Highlights
Introduction to normal derivatives as an important topic with applications in integration and the divergence theorem.
The normal derivative is defined in relation to the rate of change of a function in the direction normal to a surface in a 3-dimensional Euclidean space.
The importance of the Euclidean aspect of the ambient space in defining the normal derivative.
Formalizing the concept of the normal derivative through a precise definition involving a straight line parameterized in the normal direction to the surface.
The normal derivative is expressed as the ordinary derivative of a function with respect to a parameter along a line normal to the surface.
The relationship between the function defined on the surface and the ambient space coordinates is established for calculating the normal derivative.
Derivation of the normal derivative using Cartesian coordinates for simplicity, despite it being a 'wrong' approach in spirit.
Expression of the normal derivative in terms of the covariant derivative of the function and the differential characteristics of the surface.
Discussion on the second normal derivative and its relation to the curvature of the surface.
The second normal derivative is defined and related to the second derivative with respect to the normal direction.
The use of the chain rule and the properties of the ambient space in deriving the second normal derivative.
The second normal derivative expressed in terms of the second-order covariant derivative and the normal vector components.
Contemplation on the definition of the normal derivative in non-Euclidean spaces, such as on the surface of a sphere.
The relationship between the ambient Laplacian of a function and its surface Laplacian is explored.
A comprehensive derivation that connects various elements of differential geometry, including the chain rule, curvature tensor, and the second normal derivative.
The final expression relating the surface Laplacian to the ambient Laplacian, showcasing the power of tensor calculus.
Reflection on the process of deriving the relationship between the Laplacians, emphasizing the importance of not rushing through tensor calculations.
Transcripts
Browse More Related Video
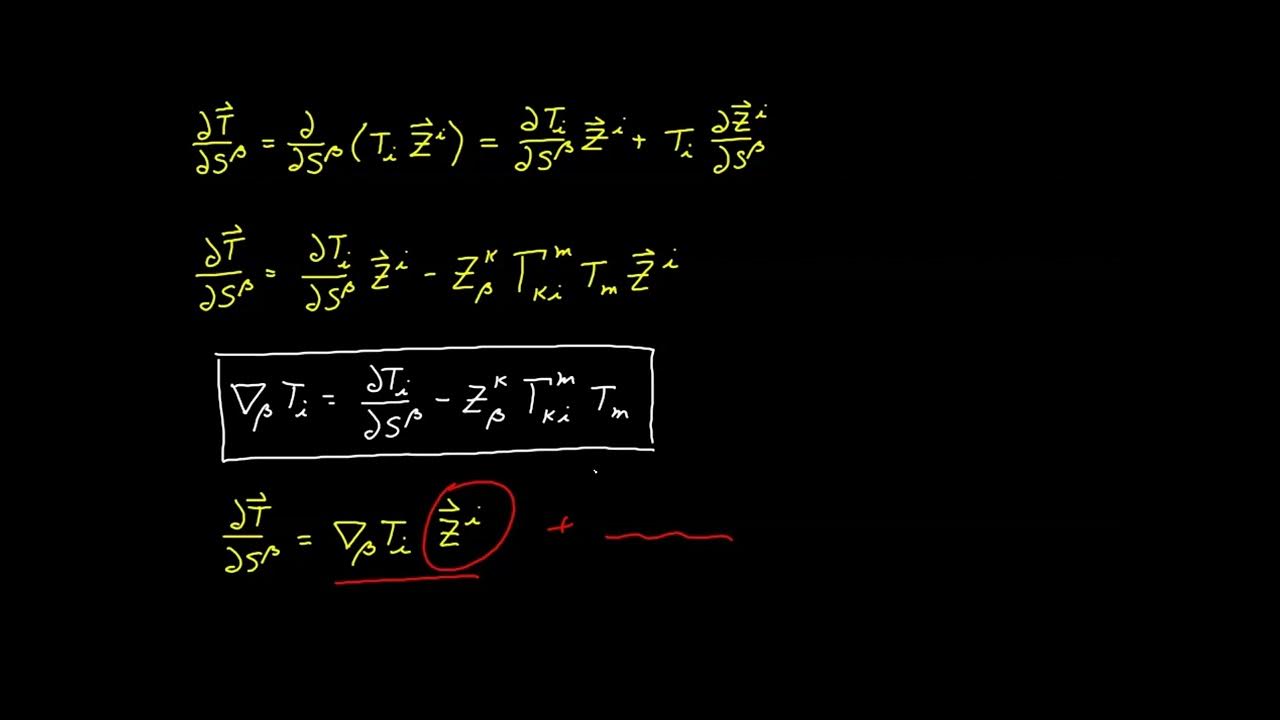
Video 72 - Surface Covariant Derivative for Non Tangent Vectors

Video 73 - Surface Covariant Derivative Properties

Video 74 - Weingarten's Formula

Tensor Calculus Lecture 13b: Integration - The Divergence Theorem
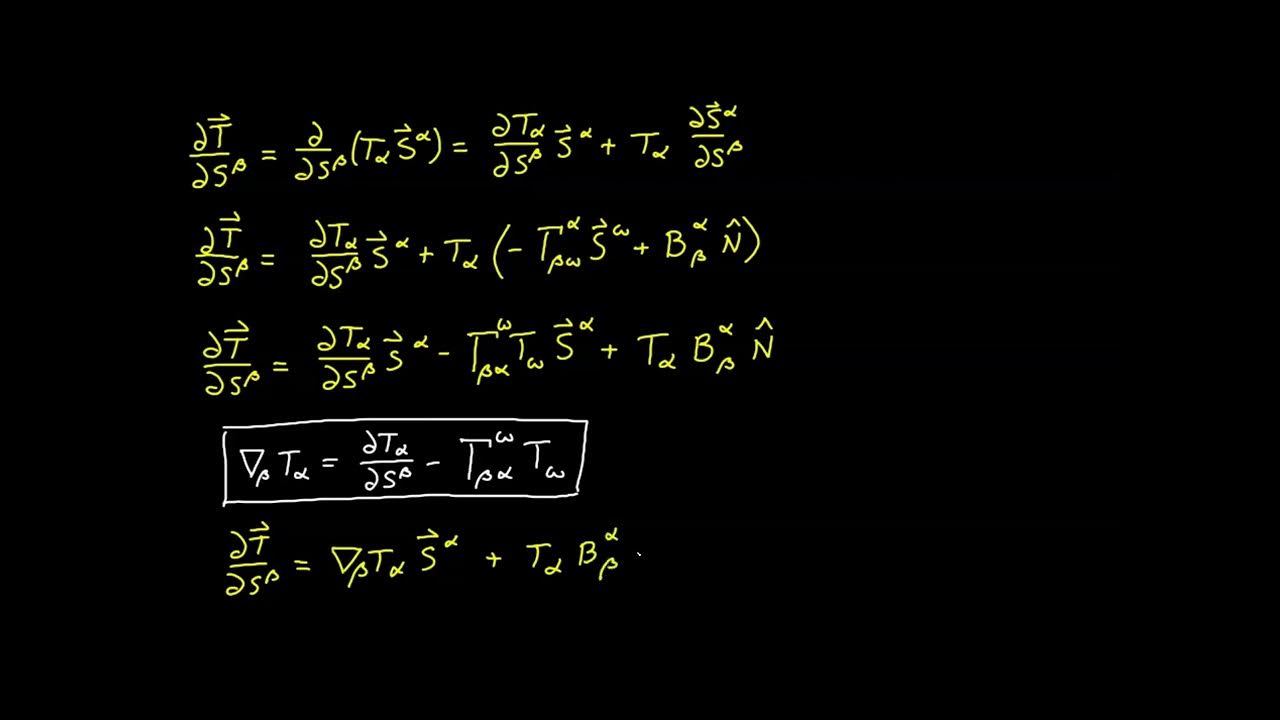
Video 71 - Surface Covariant Derivative for Tangent Vectors
Video 90 - Embedded Curves - Part 2
5.0 / 5 (0 votes)
Thanks for rating: