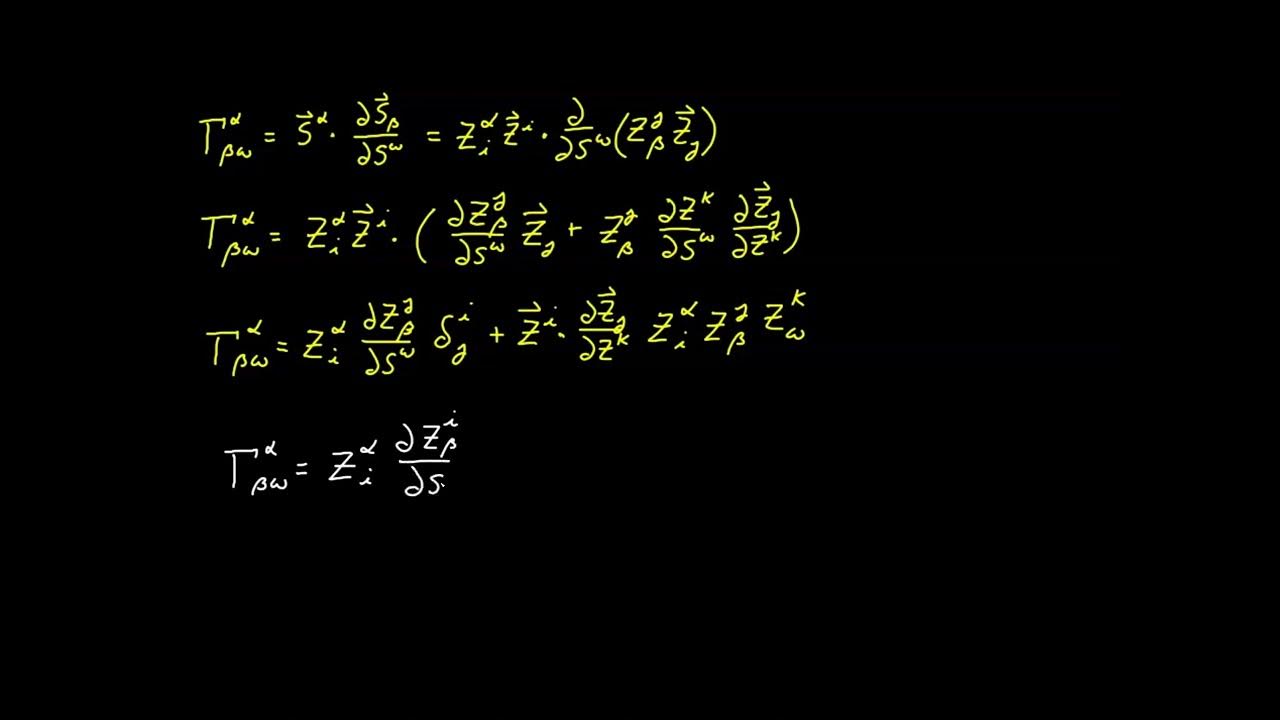Tensor Calculus 6a: The Christoffel Symbol
TLDRThis educational script delves into the intricacies of the Christoffel symbol, a fundamental concept in tensor calculus. It clarifies why the Christoffel symbol is not considered a tensor, emphasizing its role in capturing the rate of change of the metric tensor within a coordinate system. The script provides a detailed explanation of the symbol's definition, its symmetric properties, and its computation in polar coordinates. It also discusses the relationship between the Christoffel symbol and the covariant derivative, setting the stage for further exploration of tensor calculus in physics and differential geometry.
Takeaways
- 📚 The Christoffel symbol is a fundamental concept in tensor calculus, capturing the rate of change of the metric tensor within a coordinate system.
- 🔍 It is not called the Christoffel tensor because it does not behave as a tensor, despite its role in capturing changes in the coordinate system.
- 📐 In Euclidean spaces, the Christoffel symbol is defined through the covariant basis elements, which are vectors that change from one point in space to another.
- 📈 The symbol is calculated by taking the derivative of the covariant basis vectors with respect to the coordinates, resulting in a set of coefficients organized with three indices.
- 🔄 The Christoffel symbol is symmetric in its lower indices, which is a key property that simplifies calculations and understanding of coordinate transformations.
- 📝 An explicit expression for the Christoffel symbol involves taking the dot product of the derivative of the basis vectors with the covariant basis itself.
- 🌐 The script provides an example using polar coordinates, illustrating how to compute the Christoffel symbols and emphasizing their importance in understanding coordinate systems.
- 📉 The differentiation of the basis vectors and the decomposition with respect to the covariant basis yields the Christoffel symbols, which are crucial for describing the geometry of a space.
- 🧠 The script discusses the raising and lowering of indices in the context of the Christoffel symbol, highlighting different conventions used in the field.
- 🤔 It poses a thought-provoking question about the relationship between the Christoffel symbols and the differentiation of the contravariant basis, suggesting a deeper connection between these concepts.
- 🚀 The Christoffel symbol is a stepping stone towards understanding the covariant derivative, which is a central concept in differential geometry and general relativity.
Q & A
Why is the Christoffel symbol not called the Christoffel tensor?
-The Christoffel symbol is not called a tensor because it does not transform as a tensor under a change of coordinates. It is a set of coefficients that describe the rate of change of the covariant basis vectors with respect to the coordinates, and it has specific symmetries and transformation properties that distinguish it from tensors.
What is the fundamental role of the Christoffel symbol in differential geometry?
-The Christoffel symbol captures the intrinsic curvature of the space and the behavior of the coordinate system. It is used to measure the change in the metric tensor and to define the covariant derivative, which is essential for generalizing the concept of a derivative to curved spaces.
How does the Christoffel symbol relate to the covariant basis in Euclidean spaces?
-In Euclidean spaces, the Christoffel symbol is defined through the covariant basis elements. It represents the derivative of the covariant basis vectors with respect to the coordinates, which helps in understanding how the coordinate system is defined and behaves in space.
What is the significance of the symmetry property of the Christoffel symbol?
-The symmetry property, where gamma(K, I, J) = gamma(K, J, I), is important because it reflects the commutative nature of partial derivatives in Euclidean spaces. This property simplifies calculations and is a key characteristic of the Christoffel symbol.
How many non-zero components does the Christoffel symbol have in a two-dimensional polar coordinate system?
-In a two-dimensional polar coordinate system, there are only three non-zero components of the Christoffel symbol out of the eight possible components, due to the symmetry and properties of the coordinate system.
What is the explicit expression for the Christoffel symbol in terms of the covariant basis vectors?
-The explicit expression for the Christoffel symbol is given by the dot product of the derivative of the covariant basis vector Zk with respect to Zj, with the covariant basis vector Zi, which is expressed as gamma(K, I, J) = (∂Zk/∂Zj) · Zi.
Why is the Christoffel symbol crucial for defining the covariant derivative?
-The Christoffel symbol is crucial for defining the covariant derivative because it accounts for the curvature of the space and the non-commutative nature of derivatives in curved spaces. It allows for the generalization of the derivative concept to spaces where the standard derivative does not apply.
How does the Christoffel symbol help in understanding the behavior of vectors in polar coordinates?
-The Christoffel symbol helps in understanding how the basis vectors in polar coordinates change as one moves through the space. It provides information about the rate of change of these vectors with respect to the radial and angular coordinates, which is essential for vector calculus in polar systems.
What is the relationship between the Christoffel symbol and the metric tensor?
-The Christoffel symbol is related to the metric tensor through its role in capturing the change in the covariant basis vectors, which in turn affect the metric tensor. It can be seen as a measure of how the metric tensor changes with respect to the coordinates in the space.
How can the Christoffel symbol be used to differentiate between the properties of different coordinate systems?
-The Christoffel symbol can be used to differentiate between coordinate systems by examining the rates of change of the basis vectors. Different coordinate systems will have different Christoffel symbols, reflecting their unique geometric properties and how they describe space.
Outlines
📚 Introduction to the Christoffel Symbol
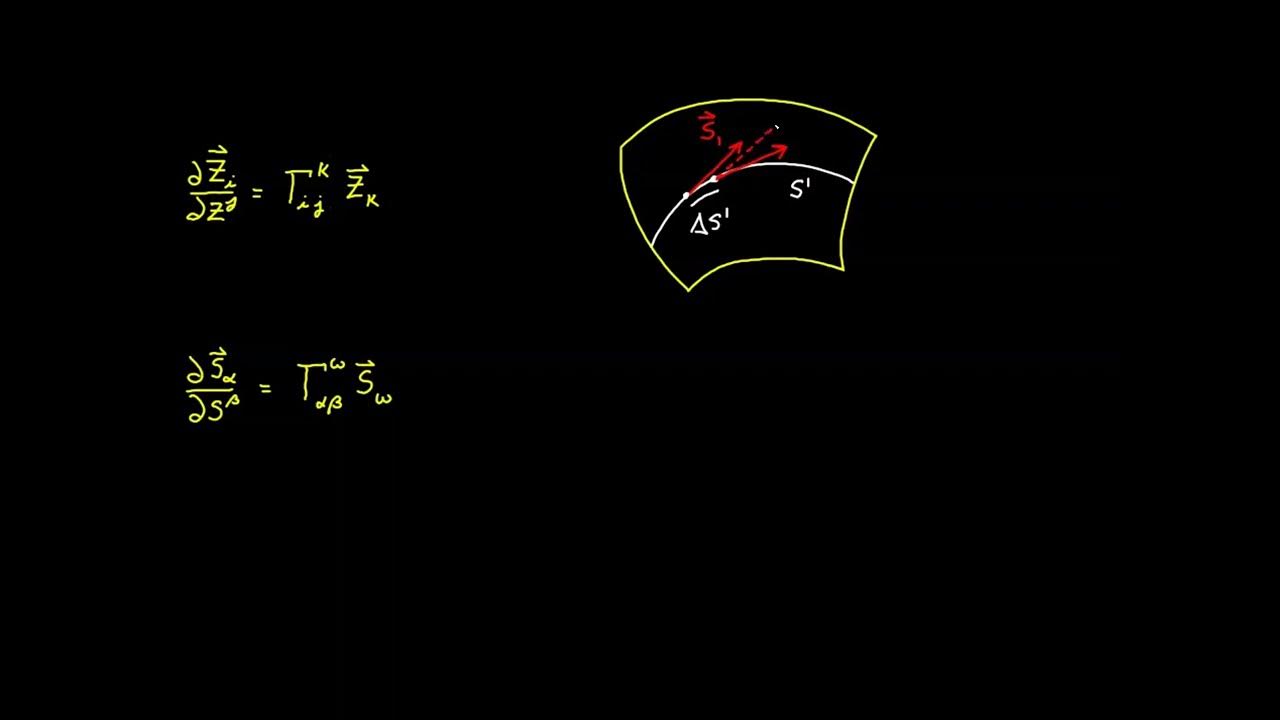
The first paragraph introduces the Christoffel symbol, a fundamental concept in tensor calculus. It clarifies that the symbol is not a tensor and explains its role in capturing the rate of change of the metric tensor within a coordinate system. The paragraph uses the example of Euclidean spaces and the covariant basis to define the Christoffel symbol. It also discusses the symmetry property of the symbol and its relation to the coordinate system's behavior, particularly in polar coordinates. The explanation includes the differentiation process of the covariant basis vectors and the resulting coefficients that form the Christoffel symbol.
🔍 Deep Dive into the Christoffel Symbol in Polar Coordinates
This paragraph delves deeper into the computation of the Christoffel symbol using polar coordinates as an example. It explains the process of differentiating the covariant basis vectors with respect to each variable, resulting in nine vectors in three dimensions. The paragraph discusses the decomposition of these vectors with respect to the covariant basis, leading to 27 coefficients organized as the Christoffel symbol with three indices. It also addresses the symmetry of the symbol and its implications for the coordinate system's properties, specifically in the context of polar coordinates.
📐 Understanding the Christoffel Symbol's Components in Polar Coordinates
The third paragraph continues the discussion on the Christoffel symbol in polar coordinates, focusing on the components of the symbol. It describes the process of determining the components gamma 1,1,1 and gamma 2,1,1, highlighting their importance in understanding the vector's behavior as it moves radially away from the origin. The paragraph also explores the rate of change of the basis vectors and how they decompose with respect to the covariant basis, leading to the identification of non-zero components of the Christoffel symbol.
🌐 Exploring the Vectorial Behavior of the Christoffel Symbol
In this paragraph, the discussion shifts to the behavior of vectors as they relate to the Christoffel symbol. It examines the rotation and length changes of vectors such as e_r and e_theta in polar coordinates, and how these changes are captured by the Christoffel symbol. The paragraph explains the rate of change of these vectors with respect to radial distance and angle, and how these rates are represented by the non-zero components of the symbol. It also touches on the surprising similarity between the components of different vectors in the context of the Christoffel symbol.
🔗 The Relationship Between the Christoffel Symbol and Metric Tensor
The final paragraph ties the Christoffel symbol to the metric tensor, emphasizing its importance in understanding the coordinate system's behavior. It suggests that the metric tensor captures the rate of change of the position vector with respect to coordinates, while the Christoffel symbol captures the change in that rate. The paragraph also addresses the possibility of differentiating the contravariant basis to obtain new vectors and their potential relationship to the Christoffel symbol. It concludes by transitioning to the topic of the covariant derivative, setting the stage for further exploration.
Mindmap
Keywords
💡Christoffel Symbol
💡Tensor Calculus
💡Covariant Basis
💡Metric Tensor
💡Polar Coordinates
💡Covariant Derivative
💡Symmetric
💡Basis Elements
💡Euclidean Spaces
💡Unit Vector
💡Differentiation
Highlights
The Christoffel symbol is a fundamental concept in tensor calculus, capturing the rate of change of the metric tensor within a coordinate system.
The Christoffel symbol is not called a tensor due to its specific properties and the way it is defined in the context of coordinate systems.
In Euclidean spaces, the Christoffel symbol is best defined through the covariant basis elements, reflecting changes in the coordinate system.
The symbol is constructed by differentiating the covariant basis vectors with respect to each variable, resulting in 27 coefficients organized with three indices.
The Christoffel symbol is symmetric in its lower indices, with gamma K IJ equal to gamma KJ I, which is a key property discussed.
The symmetry of the Christoffel symbol is tied to the inherent properties of the coordinate system, such as the relationship between dr and dθ in polar coordinates.
An explicit expression for the Christoffel symbol is given by the dot product of the differentiated vector with the covariant basis vector.
The computation of the Christoffel symbol for a polar coordinate system is demonstrated, highlighting the process for two-dimensional cases.
The significance of the Christoffel symbol in understanding the coordinate system's behavior is emphasized, particularly in relation to the metric tensor.
Only three of the eight possible components of the Christoffel symbol in a polar coordinate system are non-zero, showcasing the simplicity of nice symmetric coordinate systems.
The metric tensor and covariant basis are fundamental in capturing the rate of change of position vectors with respect to coordinates.
The Christoffel symbol represents the second derivative of the position vector's change with respect to coordinates, highlighting its importance.
The ability to raise and lower indices of the Christoffel symbol is discussed, adhering to specific conventions used in the field.
Differentiating the contravariant basis could yield a new set of 27 numbers related to the Christoffel symbol, prompting further exploration of their relationship.
The practical applications and theoretical implications of the Christoffel symbol are suggested for further discussion, particularly in the context of covariant derivatives.
The transcript concludes with an eagerness to move beyond the theoretical discussion of the Christoffel symbol to its practical applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: