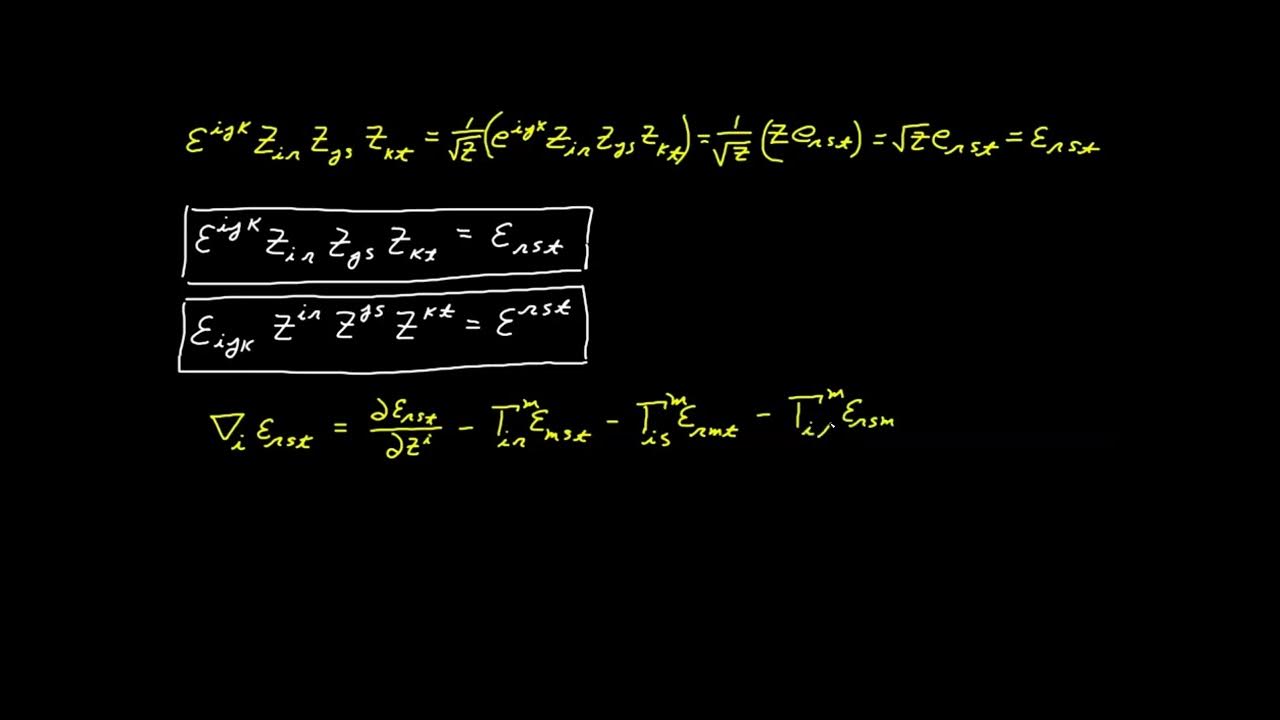Tensor Calculus Lecture 7c: The Levi-Civita Tensors
TLDRThis script delves into the concept of the Levi-Civita symbol, or tensor, highlighting its importance in tensor calculus and its relation to geometrically meaningful definitions such as the vector product and curl. The lecture explains how the symbol is formed, its properties, and its significance in defining absolute tensors. It also touches on the Levi-Civita symbol's relationship with index juggling and its metronic property, which is crucial for understanding its role in differential geometry and calculus.
Takeaways
- 📚 The script discusses the concept of 'Levi-Civita symbols', also known as 'Levi-Civita tensors', which are fundamental in tensor calculus.
- 👤 Levi-Civita, one of the co-founders of tensor calculus, had this symbol named in his honor due to his significant contributions to mathematics and geometry.
- 🔍 The Levi-Civita symbol is formed by dividing the permutation symbol by the square root of the determinant of the covariant metric tensor, resulting in an absolute tensor.
- 🔢 The script explains that the permutation symbol is a relative tensor of weight 1, while the square root of the determinant of the metric tensor is a relative tensor of weight -1.
- 📐 The Levi-Civita symbol is essential for defining geometrically meaningful operations such as the vector product and curl, which are related to determinants.
- 🔗 The script highlights the relationship between the Levi-Civita tensors and the permutation symbol through index juggling, proving that they are indeed tensors.
- 📝 The combination of two Levi-Civita symbols results in the Kronecker delta, a tensor that is used to simplify equations in various mathematical contexts.
- 📚 The script mentions the metronic property of the Levi-Civita symbol, which involves the covariant derivative and is zero for all metrics in a Riemannian space.
- 🔍 The script suggests that the Levi-Civita symbol has a natural property, which is also true for the symbol with upper indices, and is part of the tensor calculus differentiation table.
- 🔄 The script indicates that the Levi-Civita symbols will be discussed in more detail in future lectures, particularly in relation to the vector product and curl.
- 🎓 The lecture concludes with an invitation to learn more about the Levi-Civita symbol and its applications in the upcoming lecture on the 'beautiful F-theory'.
Q & A
What is the significance of the term 'Levi-Civita symbols' in the context of tensor calculus?
-The Levi-Civita symbols, also known as tensors, are fundamental objects in tensor calculus that are used to define geometrically meaningful operations such as the vector product and curl. They are named after the mathematician Tullio Levi-Civita, who co-founded the subject of tensor calculus with his teacher Gregorio Ricci-Curbastro.
Why was the term 'absolute differential calculus' used historically for tensor calculus?
-The term 'absolute differential calculus' was used because the results of the calculations did not depend on the choice of coordinate system, hence 'absolute', reflecting the intrinsic properties of the space being studied.
What is the relationship between the permutation symbol and the Levi-Civita symbol?
-The Levi-Civita symbol is formed by dividing the permutation symbol by the square root of the determinant of the covariant metric tensor. This division results in an absolute tensor, which is invariant under coordinate transformations.
What is the weight of the permutation symbol and how does it relate to the Levi-Civita symbol?
-The permutation symbol has a weight of 1, and when combined with the square root of the determinant of the metric tensor (which has a weight of -1), it results in a tensor of weight 0, which is the Levi-Civita symbol.
How are the Levi-Civita symbols used to define the vector product and curl?
-The Levi-Civita symbols are used in the definitions of the vector product and curl because they are tensors that can provide geometrically meaningful and invariant definitions, unlike non-tensors which do not lead to invariance.
What property of the Levi-Civita symbols allows them to be related by index juggling?
-The Levi-Civita symbols possess the property of being fully related by index juggling, which means that when you lower or raise indices using the metric tensor, the resulting symbols are still Levi-Civita symbols, maintaining their tensorial nature.
What is the significance of the relationship between the two Levi-Civita symbols when combined?
-When two Levi-Civita symbols are combined, they produce the Kronecker delta symbol, which is another tensor. This relationship is a proof of the tensorial nature of the Levi-Civita symbols and is useful in various tensor operations.
What is the metronic property mentioned in the script, and how does it relate to the Levi-Civita symbols?
-The metronic property refers to the fact that the covariant derivative of the Levi-Civita symbols is zero. This property is true for all metrics in Riemannian space and is an important characteristic of the Levi-Civita symbols in the context of tensor calculus.
Why is it important to discuss the Levi-Civita symbols in the context of tensor calculus?
-The Levi-Civita symbols are important to discuss in tensor calculus because they are fundamental to defining and understanding geometric operations such as the vector product and curl, and they exhibit key tensorial properties like invariance and the metronic property.
What is the connection between the Levi-Civita symbols and the Fock-Vilenkin theory mentioned in the script?
-The script mentions that the next lecture will discuss the Fock-Vilenkin theory, which is a geometric theory that may involve the use of Levi-Civita symbols for its formulation and understanding of geometric structures.
Outlines
📚 Introduction to Levi-Civita Symbols and Tensors
This paragraph introduces the Levi-Civita symbols, which are actually tensors, and therefore more appropriately referred to as such. The lecture pays homage to Levi-Civita, a renowned mathematician and geometer, who co-founded tensor calculus with his teacher Ricci. The absolute differential calculus was named 'absolute' because it was coordinate system independent. The paragraph explains the formation of the Levi-Civita symbol, denoted by 'Epsilon i j k', as a tensor resulting from the division of a relative tensor of weight -1 (the square root of the determinant of the covariant metric tensor) by a relative tensor of weight 1 (the permutation symbol). It also touches on the importance of these tensors in defining vector products and curl in a geometrically meaningful way, as opposed to non-tensor objects which lack invariance. The paragraph concludes with the mention of a few relationships that these tensors satisfy and their significance in future discussions on vector products and curl.
🔍 Analysis of Levi-Civita Tensors and Their Properties
The second paragraph delves deeper into the analysis of Levi-Civita tensors, focusing on their relationships and properties. It begins with a proof demonstrating that the Levi-Civita tensors are indeed related by index juggling, showing that lowering each of the indices in the tensor results in the permutation symbol. The paragraph then explores the combination of two Levi-Civita symbols, revealing that they combine to produce the Delta symbol, which is a full tensor. This relationship is highlighted as a proof of the tensorial nature of the Levi-Civita symbols. The paragraph also mentions the metronic property, which states that the covariant derivative of the Levi-Civita symbol is zero for all metrics in the Riemannian space. This property, along with the Levi-Civita symbol's natural property, is suggested to be part of the tensor calculus differentiation table, indicating its fundamental role in the subject. The paragraph concludes with a promise to revisit the topic in greater detail in future lectures, particularly focusing on the derivative of the Levi-Civita symbol.
Mindmap
Keywords
💡Tensor
💡Levi-Civita Symbol
💡Tensor Calculus
💡Absolute Differential Calculus
💡Covariant Metric Tensor
💡Relative Tensor
💡Vector Product
💡Curl
💡Index Juggling
💡Metric Tensor
💡Metric Space
Highlights
Introduction to the concept of Leevid symbols, which are tensors, and their significance in tensor calculus.
Historical context provided on the co-founders of tensor calculus, including Levi-Civita and his teacher Ricci.
Explanation of the term 'absolute differential calculus' and its implications for coordinate system independence.
The importance of the permutation symbol and its role as a relative tensor of weight one.
The determinant of the covariant metric tensor and its properties as a relative invariant of weight -2.
Formation of the Levi-Civita symbol through division of relative tensors of different weights.
The significance of the Levi-Civita symbol in defining the vector product and curl.
Discussion on the properties of tensors and their suitability for geometrically meaningful definitions.
The relationship between the Levi-Civita symbol and the permutation symbol through index juggling.
Proof that the Levi-Civita tensors are related by index manipulation.
Combination of two Levi-Civita symbols to produce the Delta symbol, demonstrating tensor properties.
The metronic property of the Levi-Civita symbol and its implications for tensor calculus.
The natural property of the Levi-Civita symbol with upper indices and its relation to the metronic property.
The Levi-Civita symbol's role in defining geometric and physically meaningful operations.
The future discussion on vector products and curls in relation to the Levi-Civita symbol.
The importance of understanding the derivative of the Levi-Civita symbol in tensor calculus.
Upcoming lecture on the F vielbein Theory and its connection to the Levi-Civita symbols.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: