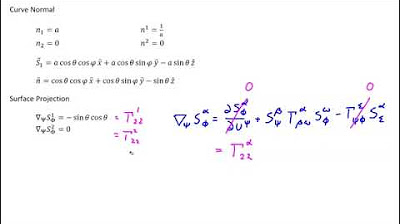Tensor Calculus Lecture 8b: The Surface Derivative of the Normal
TLDRThis lecture delves into the application of tensor calculus to differential geometry, focusing on the curvature tensor of embedded surfaces. It introduces the covariant derivative and explores its application to the normal vector and curvature tensor. The lecture also emphasizes the importance of choosing appropriate coordinate systems and the impact of normal vector selection on curvature calculations. A notable inclusion is the discussion of a sculpture by Gary S., symbolizing embedded surfaces and the elegance of coordinate systems in differential geometry.
Takeaways
- 📚 The lecture continues the discussion on embedded surfaces and the curvature tensor, emphasizing the application of tensor calculus in differential geometry.
- 🔍 The focus is on the curvature tensor, which has been introduced extrinsically and is dependent on the surface's embedding in the ambient space.
- 📈 The lecture will develop the tensor calculus further, particularly the covariant derivative's application to the normal vector and the curvature tensor itself.
- 🎨 A sculpture by Philadelphia artist Gary Smith is highlighted as a representation of embedded surfaces and the use of coordinate systems in their depiction.
- 📏 The importance of choosing an appropriate coordinate system for a given problem is underscored, with the sculpture serving as an example of an elegant choice.
- 📝 The script reviews the objects introduced so far, such as the position vector, covariant basis, metric tensor, and Christoffel symbols, which are fundamental to the study of embedded surfaces.
- 🔧 The covariant derivative is discussed in relation to the basis elements and the metric tensors, with the property that its derivative with respect to these tensors yields zero.
- 📉 The curvature tensor is derived from the observation that the covariant derivative does not annihilate the basis elements due to curvature, leading to its definition involving the normal vector.
- 🧭 The derivative of the normal vector is explored, revealing that it lies in the tangent space and is a linear combination of the basis vectors, with coefficients given by the curvature tensor.
- 🔗 The relationship between the choice of normal and the curvature tensor is emphasized, noting that the curvature tensor's values depend on the chosen normal vector.
- 🌐 The final part of the lecture aims to calculate the curvature tensor for a sphere of radius R, using the derived formulas and emphasizing the importance of consistency in the choice of normal.
Q & A
What is the main focus of the lecture?
-The main focus of the lecture is the curvature tensor in the context of differential geometry, particularly its application and the development of tensor calculus on surfaces.
Why is tensor calculus introduced in the course on differential geometry?
-Tensor calculus is introduced in the course on differential geometry because it is one of the best tools for dealing with concepts in differential geometry, especially when it comes to the curvature tensor.
What is an embedded surface and how does it relate to the lecture?
-An embedded surface is a surface that is embedded within a higher-dimensional space. The lecture discusses the curvature tensor in relation to embedded surfaces, emphasizing the importance of the extrinsic curvature and the embedding of the surface in the ambient space.
What is the significance of introducing a coordinate system in the ambient space?
-Introducing a coordinate system in the ambient space is significant for calculating the curvature tensor and for applying tensor calculus to the normal vector and the curvature tensor itself. It is also necessary for deriving explicit relationships for the normal vector.
What is the covariant derivative and why is it important in the lecture?
-The covariant derivative is a generalization of the partial derivative that takes into account the curvature of the space. It is important in the lecture because it is used to calculate the derivative of the normal vector and to develop further tensor calculus on surfaces.
How is the normal vector defined in the context of the lecture?
-In the context of the lecture, the normal vector is defined by its orthogonality to the tangent space of the surface, meaning it is orthogonal to each element of the covariant basis that spans the tangent space.
What is the significance of the choice of normal vector in the calculation of the curvature tensor?
-The choice of normal vector is significant because the curvature tensor and the mean curvature can depend on this choice. If the normal is flipped, the entries of the curvature tensor change their signs, indicating that the curvature measures are relative to the chosen normal.
What is the relationship between the covariant derivative of the normal vector and the curvature tensor?
-The covariant derivative of the normal vector is proportional to the curvature tensor. This relationship shows that the derivative of the normal lies in the tangent space, and the coefficients of this linear combination are given by the entries of the curvature tensor.
Why is it important to have a rule for differentiating every important object in tensor calculus?
-It is important to have a rule for differentiating every important object in tensor calculus to ensure that the technique is comprehensive and systematic. This allows for the consistent application of tensor calculus to various objects, such as the basis, the normal, and the curvature tensor.
How does the lecturer plan to calculate the curvature tensor of a sphere of radius R?
-The lecturer plans to use the expression derived for the covariant derivative applied to the normal vector, which is proportional to the curvature tensor. This expression will be used to calculate the curvature tensor for a sphere of radius R, taking advantage of the simplicity of the shape.
Outlines
📚 Introduction to Curvature Tensor and Tensor Calculus
The lecture begins by delving into the application of tensor calculus to differential geometry, focusing on the curvature tensor. The speaker introduces the concept of an embedded surface and its relation to tensor calculus without the need for an ambient space coordinate system. The lecture aims to further develop tensor calculus on surfaces, including the covariant derivative and its application to the normal vector and curvature tensor, which are yet to be derived. A contemporary sculpture by Gary Smith is highlighted as a representation of embedded surfaces and the importance of choosing appropriate coordinate systems.
🔍 Deriving Covariant Derivatives and Curvature Tensor
This paragraph continues the discussion on tensor calculus, specifically addressing the covariant derivative and its application to the metric tensor, which results in zero. The determinant of the covariant metric tensor and its relation to the area element are introduced, leading to the definition of the permutation symbols in the context of a two-dimensional surface. The curvature tensor is defined through the derivative of a basis element, which is proportional to the normal vector, with the proportionality constant being the curvature tensor itself. The paragraph emphasizes the need for a calculus technique to differentiate every important object, such as the basis, normal, and curvature tensor, and begins to explore the covariant derivative applied to the normal vector.
📘 Exploring the Derivative of the Normal Vector
The focus shifts to understanding the covariant derivative of the normal vector. It is established that the normal is orthogonal to each basis element of the tangent space. The paragraph explores the derivative of the normal vector using the covariant derivative, which is shown to lie in the tangent space. The coefficients of this derivative are identified as the components of the curvature tensor, highlighting the relationship between the derivative of the normal and the curvature tensor. The importance of the choice of normal is discussed, as it affects the signs of the curvature tensor components.
📐 The Orthogonality of Vector Derivatives and Tangent Space
The lecture continues with a detailed exploration of the orthogonality principle, where a vector's rate of change is orthogonal to itself if it maintains its length. This principle is applied to the derivative of the normal vector, which is shown to have no normal component, indicating that it lies entirely within the tangent space. The curvature tensor is identified as the linear combination coefficients of the derivative of the normal with respect to the covariant basis, reinforcing the connection between the derivative of the normal and the curvature tensor.
🧩 Systematic Derivation of the Normal Vector's Coefficients
The speaker systematically derives the coefficients of the normal vector in the tangent space, using the covariant derivative and the orthogonality principle. The process involves dotting both sides of the identity with the normal vector, leading to the discovery that the coefficients are zero in the normal direction. The coefficients in the tangential direction are then determined by further manipulation of the identity, revealing the relationship between the coefficients and the curvature tensor.
📉 The Curvature Tensor as a Linear Combination of Basis Vectors
The paragraph concludes the derivation by identifying the coefficients of the normal vector's derivative with respect to the covariant basis as the negative entries of the curvature tensor. This finding is encapsulated in a formula that elegantly expresses the derivative of the normal vector in terms of the tangent space basis and the curvature tensor. The importance of the choice of normal is reiterated, as it affects the direction and magnitude of the curvature tensor.
🌐 Calculation of the Curvature Tensor for a Sphere
The final paragraph outlines the intention to calculate the curvature tensor for a sphere of radius R using the derived expressions. The speaker emphasizes the preference for using a covariant derivative applied to an invariant, as it simplifies calculations by avoiding the need for Christoffel symbols. The paragraph concludes with a note on the importance of index juggling in tensor calculus, especially when dealing with symmetric tensors like the metric and curvature tensors.
Mindmap
Keywords
💡Embedded Surfaces
💡Curvature Tensor
💡Tensor Calculus
💡Covariant Derivative
💡Normal Vector
💡Christoffel Symbols
💡Metric Tensor
💡Contravariant Basis
💡Levi-Civita Symbol
💡Euclidean Space
💡Differential Geometry
Highlights
Introduction of tensor calculus in differential geometry as a powerful tool.
Curvature tensor as the central focus, introduced extrinsically based on the surface's embedding in space.
Discussion on the necessity of introducing a coordinate system in the ambient space for further tensor calculus development.
Covariant derivative's role in tensor calculus and its application to the normal vector and curvature tensor.
The importance of choosing an appropriate coordinate system for problem-solving in differential geometry.
Christoffel symbols and their definition in relation to the covariant basis and metric tensors.
Properties of the covariant basis and its derivative with respect to the metric tensors, leading to zero results.
Introduction of the permutation symbols and their relation to the area element in two-dimensional surfaces.
The definition and properties of the curvature tensor in relation to the derivative of a basis element.
The need for a rule in tensor calculus for differentiating every important object, such as the basis and normal.
Derivation of the covariant derivative applied to the normal vector and its significance in the tangent space.
The relationship between the normal vector's derivative and the curvature tensor, highlighting the minus sign's importance.
The impact of the choice of normal on the curvature tensor and the necessity for consistency in calculations.
The explicit relationship for the curvature tensor in terms of the derivative of the normal and its dependency on the choice of normal.
The practical application of the derived formula in calculating the curvature tensor of a sphere of radius R.
The importance of index juggling in tensor calculus due to the covariant derivative's metronomic property.
The preference for using covariant derivatives applied to invariants for simplifying calculations by hand.
The significance of the curvature tensor in differential geometry and its dependence on the choice of normal vector.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: