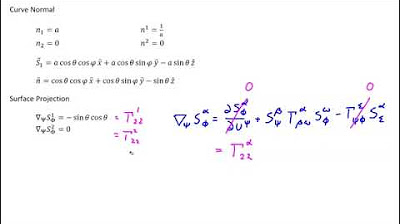Tensor Calculus Lecture 9b: The Components of the Normal Vector
TLDRThis video script delves into the mathematical derivation of the normal vector in the context of differential geometry, focusing on its relationship with the shift tensor. The presenter explains how the normal, being orthogonal to the tangent plane, can be expressed using the shift tensor. They introduce an explicit formula for the normal vector, discuss its properties, and guide viewers through the proof of these properties, emphasizing the importance of understanding tensor notation and permutation symbols in this process. The script concludes with an invitation for viewers to complete the proof as an exercise, highlighting the educational and interactive nature of the content.
Takeaways
- 📚 The script discusses the derivation of the normal vector's expression in terms of the shift tensor, which is an important concept in differential geometry.
- 📐 The normal vector is orthogonal to the tangent plane and can be expressed using the shift tensor, highlighting the relationship between the two.
- 🔍 The provided expression for the normal vector is not frequently used but is valuable for understanding its properties and for differentiation purposes.
- 🌐 The normal vector is defined implicitly by being of unit length and orthogonal to the shift tensor, which is a key point in its definition.
- ⚙️ The script introduces the concept of covariant basis vectors in the tangent plane and their role in defining the normal vector.
- 📉 The normal vector's expression involves the cross product of two basis vectors in the tangent plane, adjusted for unit length and sign ambiguity.
- 📝 The explicit formula for the normal vector in a three-dimensional ambient space with a two-dimensional surface is derived using tensor notation.
- 🔢 The derivation involves the use of the Levi-Civita symbol (Epsilon) and the metric tensor components, which are fundamental in tensor calculus.
- 🔄 The script emphasizes the importance of proving two key properties of the normal vector: orthogonality to the covariant basis and unit length.
- 📚 The proof involves permutation symbols and the properties of the Levi-Civita symbol, demonstrating the complexity of tensor operations.
- 🎯 The final expression for the normal vector is given as a combination of the Levi-Civita symbol, the metric tensor components, and a normalization factor.
Q & A
What is the relationship between the normal vector and the shift tensor in differential geometry?
-The normal vector is orthogonal to the tangent plane, which is described by the shift tensor. The normal vector can be expressed in terms of the shift tensor, and although this expression is not commonly used, it provides an explicit identity for the normal vector.
Why is the normal vector often described as the cross product of two basis vectors in the tangent plane?
-The normal vector is often described as the cross product of two basis vectors in the tangent plane because the cross product naturally produces a vector orthogonal to the plane formed by the two vectors. This method is useful, but it requires ensuring that the resulting vector is of unit length.
What is a disadvantage of using tensor notation when working with the normal vector in different dimensions?
-A disadvantage of using tensor notation is that the expression for the normal vector needs to be adjusted for each dimension. This makes the process less straightforward compared to other methods like using the cross product.
How does the introduction of the Levi-Civita symbol help in expressing the normal vector?
-The Levi-Civita symbol is used to express the cross product in tensor notation. By contracting the shift tensor components with the Levi-Civita symbol, the formula for the normal vector can be derived, ensuring that it is of unit length and properly oriented.
Why is it necessary to divide the derived expression for the normal vector by 2?
-The expression is divided by 2 to account for the fact that the Levi-Civita symbol introduces a factor of 2 when summing over the two possible permutations of the basis vectors. This ensures that the normal vector is correctly normalized.
What role does the permutation symmetry of the Levi-Civita symbol play in deriving the normal vector?
-The permutation symmetry of the Levi-Civita symbol ensures that the expression for the normal vector is antisymmetric in its indices. This antisymmetry is crucial for the proper cancellation of terms, which leads to the correct expression for the normal vector.
How does the expression for the normal vector ensure that it is of unit length?
-The expression for the normal vector inherently ensures unit length by normalizing the result of the cross product. The use of the Levi-Civita symbol and the division by 2 factor contribute to this normalization.
Why is it important to verify the properties of the normal vector after deriving its explicit expression?
-Verifying the properties of the normal vector, such as its orthogonality to the tangent plane and its unit length, ensures that the derived expression is correct and consistent with the geometric interpretation of the normal vector.
What is the significance of the Delta symbol in the context of verifying the normal vector's properties?
-The Delta symbol (Kronecker delta) is used to simplify the expressions during the verification process. It helps in contracting indices and reducing complex tensor expressions, ensuring that the derived properties of the normal vector hold true.
Why is it useful to prove the projection property of the normal vector as an exercise?
-Proving the projection property of the normal vector helps reinforce understanding of tensor calculus and the relationships between different geometric objects. It also provides a deeper insight into the role of the normal vector in the context of differential geometry.
Outlines
📚 Deriving the Normal Vector Expression
The first paragraph delves into the mathematical derivation of the normal vector in relation to the shift tensor. It explains that the normal is orthogonal to the tangent plane and can be expressed using the shift tensor. The speaker acknowledges that the explicit expression for the normal is not commonly used due to its implicit definition through unit length and orthogonality. The paragraph introduces the concept of using the cross product of two basis vectors in the tangent plane to define the normal, with an emphasis on the need for unit length and handling the sign ambiguity that arises from the cross product's order of vectors.
🔍 Guaranteeing Unit Length for the Normal Vector
In the second paragraph, the discussion continues with refining the expression for the normal vector to ensure it is of unit length. The speaker introduces a method to eliminate the explicit indices by using the surface's epsilon symbol, which leads to a more elegant tensor notation. The resulting formula for the normal vector is presented, and the speaker suggests that the audience should verify two key properties: orthogonality to the shift tensor and unit length, as an exercise. The paragraph concludes with a preview of the proof for these properties, emphasizing the importance of understanding permutation symbols and symmetric properties.
📘 Proving the Normal Vector Expression Through Tensor Notation
The third paragraph focuses on the proof of the normal vector's explicit expression using tensor notation. The speaker outlines a complex proof involving epsilon symbols and shift tensors, highlighting the importance of contraction and permutation in tensor calculus. The paragraph provides a partial proof and invites the audience to complete it, emphasizing the satisfaction of seeing how the indices are renamed and how terms simplify through contractions. The speaker assures that the proof, despite its complexity, is rewarding and provides a deeper understanding of tensor operations.
📌 Final Thoughts on the Normal Vector Expression
The final paragraph wraps up the discussion on the normal vector's expression, inviting the audience to complete the proof as a sanity check and to reinforce the understanding of the normal vector's properties. The speaker briefly touches upon the geometric considerations that validate the expression and encourages the audience to accept the derived formula based on its geometric and algebraic soundness. The paragraph concludes with a transition to the next topic, the chain rule for covariant differentiation, and thanks the audience for their attention.
Mindmap
Keywords
💡Shift Tensor
💡Normal Vector
💡Tangent Plane
💡Covariant Basis
💡Orthogonality
💡Cross Product
💡Unit Length
💡Epsilon Symbol
💡Permutation Symbols
💡Tensor Notation
💡Differential Geometry
Highlights
The normal vector is expressible in terms of the shift tensor, which describes the tangent plane.
The normal vector is defined implicitly by being unit length and orthogonal to the shift tensor.
The expression for the normal is not frequently used due to its complexity in tensor notation.
The normal is often described as the cross product of two basis vectors in the tangent plane.
The explicit expression for the normal vector is derived using the cross product of covariant basis vectors.
The normal vector must be unit length, which is achieved by dividing the cross product by its length.
The tensor notation hides the complexity of ensuring unit length for the normal vector.
The expression for the normal in three-dimensional space involves the determinant and the shift tensor components.
The normal vector is defined with respect to the sign, which can vary depending on the cross product order.
The explicit expression for the normal is derived using the Levi-Civita symbols and shift tensor components.
The proof of the normal's properties involves showing it is orthogonal to the covariant basis and has unit length.
The cross product between two vectors is expressed using the Levi-Civita symbol and the shift tensor.
The explicit indices in the cross product are replaced with tensor notation to generalize to higher dimensions.
The final expression for the normal vector includes a factor of 1/2 to account for the double counting of terms.
The proof of the normal's properties is challenging and involves working with permutation symbols and contraction relationships.
The explicit expression for the normal vector is verified through geometric considerations and tensor algebra.
The discussion concludes with the verification of the normal vector's properties and the introduction of the chain rule for covariant differentiation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: