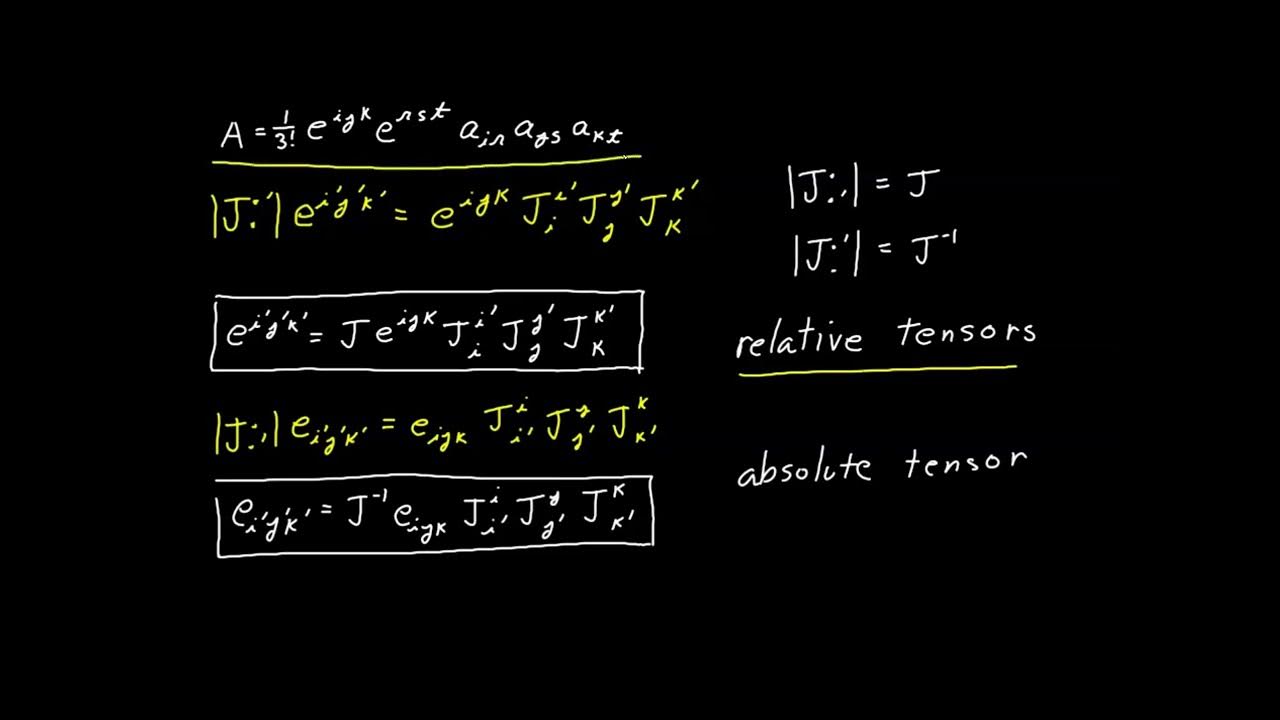Tensor Calculus Lecture 7b: Relative Tensors
TLDRThis lecture delves into the concept of relative tensors, building upon the discussion of determinants and permutation symbols. It clarifies the misconception that certain permutation symbols are related by index juggling, demonstrating through formal index manipulation that they are not. The talk explores the transformation properties of these symbols under coordinate changes, revealing them as relative tensors of different weights. The significance of the metric tensor's determinant and its role in defining relative tensors is highlighted, with the volume element introduced as a relative invariant of weight -1, crucial for volume integration.
Takeaways
- 📚 The script discusses the concept of relative tensors and permutation symbols in the context of tensor notation and transformations.
- 🔍 The speaker clarifies that permutation symbols with lower indices and without parentheses are not related by simple index juggling, contrary to what the notation might suggest.
- 🧩 It is explained that applying formal index juggling to certain symbols does not equate them to others, highlighting a common misconception in tensor notation.
- 📉 The determinant of the covariant metric tensor is shown to be related to the permutation symbol with lower indices, but with a crucial difference due to the placement of indices.
- 🔢 The concept of 'C', denoting the determinant of the metric tensor, is introduced, with a focus on its covariant form.
- 📏 The script emphasizes that permutation symbols are not tensors, which is an important distinction when considering their use in tensor notation.
- 🌐 Transformation properties of tensors are explored, specifically how permutation symbols with lower indices transform under coordinate changes.
- 🔄 The determinant of the Jacobian matrix is used to demonstrate the transformation of permutation symbols, leading to the concept of relative tensors.
- ⚖️ Relative tensors are defined as tensors with an additional factor of the determinant of the Jacobian (J) raised to a power, which constitutes the tensor's weight.
- 🔑 The script introduces the idea that the same object can be viewed as a relative tensor of both positive and negative weight, depending on whether it's considered covariant or contravariant.
- 📚 The volume element is identified as a relative tensor of weight -1, playing a central role in volume integration and having physical and geometric significance.
Q & A
What is the topic of discussion in the provided script?
-The script discusses the concept of relative tensors, specifically focusing on permutation symbols and their properties under transformations.
What are the two types of permutation symbols mentioned in the script?
-The two types of permutation symbols mentioned are with lower indices (pIJK) and without parentheses (Eijk).
What is the significance of the notation in permutation symbols?
-The notation suggests a possible relationship between different permutation symbols, particularly whether they are related by index juggling.
What is the role of the covariant metric tensor in the script's discussion?
-The covariant metric tensor is used in the expression for the determinant of the permutation symbol with lower indices, indicating its importance in tensor calculus.
What is the difference between a regular tensor and a relative tensor?
-A regular tensor is a relative tensor of weight 0. Relative tensors have an additional factor of J (the determinant of the Jacobian) raised to some power, which constitutes the weight of the tensor.
How does the permutation symbol with lower indices transform under a change of coordinates?
-The permutation symbol with lower indices transforms as a relative tensor of weight one, with an additional factor of the determinant of the Jacobian.
What is the significance of the term 'weight' in the context of relative tensors?
-The 'weight' of a relative tensor refers to the power of the Jacobian determinant that multiplies the tensor during a coordinate transformation.
What is the volume element, and how does it relate to relative tensors?
-The volume element is the square root of the determinant of the metric tensor (Z), and it is a relative tensor of weight negative one, playing a central role in volume integration.
How does the determinant of the metric tensor transform under a coordinate transformation?
-The determinant of the metric tensor transforms with a factor of the Jacobian determinant raised to the power of negative two for the covariant metric tensor and positive two for the contravariant metric tensor.
What is the significance of the sign convention in coordinate transformations mentioned in the script?
-The sign convention is important when considering coordinate transformations that do not necessarily have a positive determinant of the Jacobian, which can affect the properties of the volume element and other related quantities.
What are the Levi-Civita symbols, and how are they related to the discussion in the script?
-The Levi-Civita symbols are a specific type of permutation symbol that are used in various areas of mathematics and physics, including tensor calculus. They are related to the script's discussion as the script builds up to discussing these symbols in the context of relative tensors.
Outlines
🔍 Exploring Relative Tensors and Permutation Symbols
The script begins with an exploration of relative tensors and permutation symbols, introducing the concept of index juggling and its implications on tensor notation. It poses a warm-up question about the relationship between two types of permutation symbols, \( p_{ijk} \) and \( \epsilon_{ijk} \), and whether they can be related through index manipulation. The discussion delves into the determinant of the covariant metric tensor and its relationship with the permutation symbol, highlighting that while the notation suggests a connection, formal index juggling reveals they are not directly related. The script emphasizes the importance of understanding tensor notation and the limitations of relying solely on it.
📚 Understanding the Transformation of Permutation Symbols
This paragraph delves deeper into the transformation properties of permutation symbols, specifically when contracted with Jacobians. The goal is to determine if these objects qualify as tensors by examining their transformation under coordinate changes. The script explains that the permutation symbol with lower indices, \( \epsilon_{ijk} \), when transformed, does not yield a simple tensor but rather a tensor with an additional factor of the Jacobian determinant, \( J \). This leads to the concept of a relative tensor, which is a generalization of a regular tensor with an additional scaling factor related to the Jacobian determinant.
🌐 The Nature of Relative Tensors and Their Weights
The script clarifies the nature of relative tensors, discussing their weights and how they transform under coordinate transformations. It explains that the permutation symbol can be viewed as both a relative tensor of weight 1 (covariant) and weight -1 (contravariant), depending on the perspective. The paragraph introduces the concept of weight in relative tensors and how it affects their transformation rules. The determinant of the metric tensor and its inverse are also discussed, showing how they transform as relative tensors of weight -2 and 2, respectively.
📈 The Role of the Volume Element in Tensor Analysis
In the final paragraph, the script discusses the volume element, which is derived from the square root of the determinant of the metric tensor. It is identified as a relative tensor of weight -1 and plays a crucial role in volume integration. The script also touches on the importance of sign conventions in coordinate transformations and the conditions under which these conventions apply. The volume element is highlighted as a key concept in understanding the geometric and physical implications of tensor analysis.
Mindmap
Keywords
💡Permutation Symbols
💡Index Juggling
💡Covariant Tensors
💡Jacobian Determinant
💡Relative Tensors
💡Metric Tensor
💡Levi-Civita Symbol
💡Volume Element
💡Transformation Rules
💡Tensor Notation
Highlights
Discussion on permutation symbols and their relation through index juggling.
Exploration of whether permutation symbols with lower indices are related to those without parentheses through formal index juggling.
Clarification that the notation of permutation symbols can be misleading and does not always indicate a direct relationship through index juggling.
Introduction to the concept of relative tensors and their distinction from regular tensors.
Explanation of how permutation symbols are not tensors due to their lack of tensorial properties.
Demonstration of the transformation of permutation symbols under coordinate transformations and the emergence of relative tensors.
Identification of the permutation symbol with lower indices as a relative tensor of weight one.
Identification of the permutation symbol with upper indices as a relative tensor of weight negative one.
Discussion on the identical values of permutation symbols and their dual nature as relative tensors of different weights depending on the perspective.
Introduction to the concept of relative tensor weight and its significance in tensor analysis.
Explanation of how the determinant of the metric tensor transforms under coordinate changes and its role as a relative tensor of weight negative two.
Discussion on the volume element as a relative tensor of weight negative one and its importance in volume integration.
Clarification of sign conventions in coordinate transformations and their impact on the properties of tensors.
Introduction to the Levi-Civita symbols and their significance in tensor calculus.
Final note on the importance of considering only positive determinants of the Jacobian for certain coordinate transformations.
Summary of the key points discussed in the lecture on relative tensors and their properties.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: