Tensor Calculus 5b: Invariants Are Tensors

MathTheBeautiful
5 Mar 201409:56
EducationalLearning
32 Likes 10 Comments

TLDRThis script delves into the concept of invariants as a special case of tensors, specifically order zero tensors, which do not transform under coordinate changes due to the absence of indices. It emphasizes the importance of understanding tensor transformations and how invariants fit into the broader framework of tensor calculus. The discussion also introduces the determinant of the covariant metric tensor, denoted by 'Z', and explores its properties, including the volume element and its relevance in integral calculus for evaluating volumes in different coordinate systems.

Takeaways
  • 📚 Invariants are a type of tensor, specifically tensors of order zero, which do not transform under the application of Jacobians due to the absence of indices.
  • 🔍 The concept of tensors is introduced with the first-order contravariant tensor and the second-order covariant tensor, each transforming according to specific rules involving Jacobians.
  • 🔑 The fundamental theorem of tensor calculus is highlighted, which states that tensors remain tensors under contraction, and this principle applies to invariants as a special case.
  • 🌐 The script emphasizes that invariants, being tensors of order zero, are consistent with the transformation rules of tensors but without the need for Jacobians due to the lack of indices.
  • 📉 The determinant of the covariant metric tensor, denoted by 'Z', is identified as an invariant, which is a scalar quantity and does not vary with coordinate systems.
  • 📏 The square root of 'Z' is discussed as the volume element, which varies in different coordinate systems but is a key concept in integral calculus for volume evaluation.
  • 👉 The position vector is clarified as an invariant, not derived from a combination of covariant and contravariant components, but rather as a fundamental quantity defined by an arrow from an origin.
  • 📊 The determinant of the Kronecker Delta is presented as an invariant of order zero, which remains constant across all coordinate systems.
  • 🤔 The script challenges the notion that all scalars are invariants, providing examples to illustrate the distinction between scalars and invariants.
  • 📚 The properties of covariant derivatives are introduced, with the first property stating that covariant derivatives applied to an invariant are equivalent to partial derivatives.
  • 🛠 The discussion transitions to the properties of covariant derivatives, setting the stage for further exploration of their behavior and implications in tensor calculus.
Q & A

  • What are tensors and why are invariants considered tensors?

    -Tensors are mathematical objects that generalize scalars, vectors, and other quantities in a way that is invariant under coordinate transformations. Invariants are considered tensors of order zero because they transform consistently across different coordinate systems without any change in value, similar to how tensors transform according to their indices.

  • What is the difference between a first-order contravariant tensor and a second-order covariant tensor?

    -A first-order contravariant tensor transforms according to a specific rule when changing coordinate systems, with each index having its own transformation rule. A second-order covariant tensor also transforms according to a rule, but it involves two indices, each with its own Jacobian matrix, indicating a more complex transformation.

  • What is the fundamental theorem of tensor calculus mentioned in the script?

    -The fundamental theorem of tensor calculus states that when you contract any two indices of a tensor, the resulting object is still a tensor. The order of the resulting tensor is reduced by two, and it transforms according to the remaining indices.

  • How does the concept of invariance relate to the transformation of tensors?

    -Invariance in the context of tensors means that the value of an invariant remains the same in all coordinate systems. This is a special case of tensor transformation where there are no indices, and thus no Jacobians are involved, leading to the same value across all systems.

  • What is the significance of the determinant of the covariant metric tensor in the script?

    -The determinant of the covariant metric tensor, denoted by 'Z', is an invariant because it is a scalar quantity that does not change under coordinate transformations. It is important in various calculations, especially in integrals involving volumes in different coordinate systems.

  • Can you provide an example of an invariant that is not derived from a combination of covariant and contravariant components?

    -Yes, the determinant of the Kronecker Delta is an invariant that is not derived from a combination of covariant and contravariant components. It is one in all coordinate systems and represents an invariant of order zero.

  • What is the volume element in the context of the script, and why is it important?

    -The volume element, represented by the square root of 'Z', is an invariant that appears in integrals when evaluating volumes in different coordinate systems. It is important because it ensures the correct calculation of volumes regardless of the coordinate system used.

  • How does the position vector relate to the concept of invariance?

    -The position vector is an invariant because it represents a directed line segment from an arbitrary origin to a point in space, and its magnitude does not change under coordinate transformations. It is defined independently of the coordinate system.

  • What is the first property of the covariant derivative as mentioned in the script?

    -The first property of the covariant derivative is that when applied to an invariant, it is equivalent to the partial derivative. This property places the covariant derivative within the broader framework of tensor calculus.

  • How does the script relate the concept of invariants to the broader scheme of tensor transformations?

    -The script relates invariants to the broader scheme of tensor transformations by showing that invariants can be seen as special forms of tensors of order zero. This perspective allows all theorems that apply to tensors to also apply to invariants, providing a unified approach to understanding transformations in different coordinate systems.

Outlines
00:00
📚 Tensors and Invariants: A Mathematical Exploration

This paragraph delves into the concept of tensors and invariants in the context of coordinate transformations. It clarifies that invariants are a type of tensor, specifically of order zero, which do not change their values across different coordinate systems. The speaker introduces the transformation rules for first-order contravariant tensors and second-order covariant tensors, emphasizing the role of Jacobians in these transformations. The fundamental theorem of tensor calculus is highlighted, which states that contracting indices of a tensor results in a tensor of lower order. The discussion also touches on the special case of invariants, which, despite having no indices, still adhere to the tensor transformation rules due to the absence of Jacobians. The paragraph concludes by illustrating how invariants fit into the broader framework of tensor theory, simplifying the understanding of various theorems and their applications.

05:04
📘 The Role of the Covariant Metric Tensor and Invariants

The second paragraph provides an example of an invariant, the determinant of the covariant metric tensor, denoted by 'Z'. It discusses how this determinant is calculated and its behavior across different coordinate systems, such as Cartesian and polar coordinates. The concept of the volume element, derived from the square root of 'Z', is introduced, explaining its significance in integral calculus for volume measurements. The paragraph further explores other examples of invariants, such as the position vector and the determinant of the Kronecker Delta, and their properties. It also touches on the relationship between covariant and contravariant components in the context of tensors. The segment concludes with an introduction to the properties of covariant derivatives, specifically how they behave when applied to invariants, equating them to partial derivatives in this context.

Mindmap
Keywords
💡Invariants
Invariants are quantities that retain the same value across different coordinate systems. In the context of the video, they are a special type of tensor, specifically a tensor of order zero. This means they do not transform with Jacobians, as they have no indices. The video emphasizes that invariants fit into the broader category of tensors, highlighting their role in the fundamental theorem of tensor calculus.
💡Tensors
Tensors are mathematical objects that generalize scalars, vectors, and other quantities with respect to coordinate transformations. The video discusses tensors of different orders, such as first-order contravariant tensors and second-order covariant tensors, which transform according to specific rules involving Jacobians. Tensors are central to the discussion, as they provide the framework for understanding how quantities change under coordinate transformations.
💡Coordinate Systems
Coordinate systems are the reference frames used to describe the position and transformation of points in space. The script discusses how tensors and invariants behave when transitioning from one coordinate system to another, such as Cartesian to polar or spherical coordinates. The transformation rules are crucial for understanding the properties and calculations involving tensors.
💡Jacobian
The Jacobian is a determinant that expresses the transformation rules for tensors when moving between coordinate systems. In the script, it is mentioned that each index of a tensor has its own Jacobian, which dictates how the tensor transforms. The absence of a Jacobian for invariants is what makes them invariant across coordinate systems.
💡Covariant and Contravariant Tensors
Covariant and contravariant tensors are specific types of tensors that transform in different ways under coordinate transformations. The video script explains that a first-order contravariant tensor transforms with a specific rule, while a second-order covariant tensor has its own transformation rule. These concepts are fundamental to understanding the nature of tensor transformations.
💡Transformation Rule
A transformation rule defines how a tensor changes when the coordinate system is altered. The script mentions that tensors transform according to certain rules, which involve the use of Jacobians. The transformation rule is essential for calculating the new values of tensors in different coordinate systems.
💡Volume Element
The volume element, denoted as the square root of the determinant of the covariant metric tensor (√g), is an invariant that describes the volume in different coordinate systems. The script uses it as an example to illustrate how invariants can be calculated differently in various coordinate systems but retain the same value.
💡Metric Tensor
The metric tensor is a key concept in differential geometry, defining the geometry of a space through its components. The script refers to the covariant metric tensor, whose determinant is used to calculate the volume element. It is an example of how tensors can be used to describe the properties of space in various coordinate systems.
💡Covariant Derivative
The covariant derivative is a generalization of the derivative that is used in tensor calculus to take into account the curvature of space. The script mentions that when applied to an invariant, the covariant derivative is equivalent to the partial derivative, indicating its role in differentiating tensors and invariants in curved spaces.
💡Partial Derivative
A partial derivative is the derivative of a function with respect to one variable, holding the other variables constant. In the context of the video, it is contrasted with the covariant derivative, showing that for invariants, the covariant derivative simplifies to the standard partial derivative.
💡Kronecker Delta
The Kronecker Delta is a tensor that equals 1 if its two indices are the same and 0 otherwise. The script mentions the determinant of the Kronecker Delta as an invariant, which is always 1 in any coordinate system, demonstrating the concept of invariance in a simple tensorial context.
Highlights

Invariants are tensors of order zero, transforming consistently across coordinate systems without indices.

First-order contravariant tensors transform according to the Jacobian matrix when moving between coordinate systems.

Second-order invariants are characterized by each index having its own Jacobian during coordinate transformation.

Tensor calculus theorems can be applied to invariants as they are a special case of tensors.

Contraction of tensor indices results in tensors of lower order, maintaining the fundamental properties of tensors.

Invariants avoid transformation rules involving Jacobians due to the absence of indices.

The determinant of the covariant metric tensor, denoted by 'Z', is an example of an invariant.

The value of 'Z' varies with coordinate systems, illustrating the concept of invariants in different contexts.

Square root of 'Z' represents the volume element, crucial for integral calculations in various coordinate systems.

Invariants can arise without a combination of covariant and contravariant components, as seen with the determinant of the Kronecker Delta.

The position vector is an invariant, defined as an arrow from an arbitrary origin, independent of coordinate decomposition.

Covariant derivatives have properties that allow them to be applied to invariants, equating to partial derivatives.

The discussion emphasizes the importance of understanding the transformation properties of tensors and invariants in physics and mathematics.

Tensors and invariants are integral to the study of coordinate transformations and their implications in physical laws.

The transcript provides a clear explanation of how tensors of different orders transform and their significance in theoretical physics.

The properties of covariant derivatives are foundational in differential geometry and general relativity.

Transcripts

Browse More Related Video

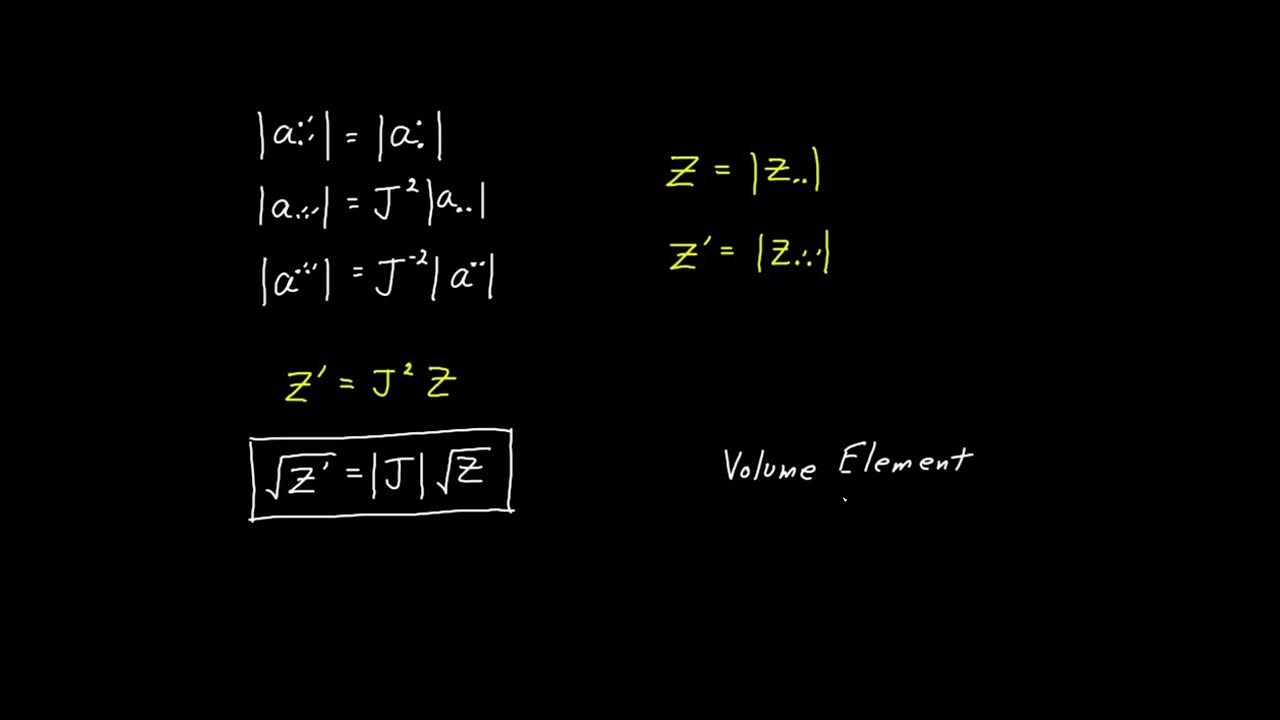
Video 48 - Volume Element

Tensor Calculus Lecture 8c: The Curvature Tensor On The Sphere Of Radius R

Tensor Calculus For Physics Majors 004| Transformation of Two Index Tensors

Tensor Calculus For Physics Majors #1| Preliminary Vector Stuff part 1

Tensor Calculus 4g: Index Juggling

Video 19 - Tensor Definition

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Tensor CalculusInvariantsCoordinate SystemsJacobian MatricesVolume ElementMetric TensorDifferential GeometryTransformation RulesContravariant TensorsCovariant Derivatives