Bases other than e

Chad Gilliland
3 Dec 201309:57
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video explores logarithmic and exponential functions beyond the base 'e', focusing on solving equations, derivatives, and integrals. It demonstrates solving equations using logarithms, converting logarithmic equations to exponential form, and applying derivatives and integrals for functions with non-e bases. The presenter also introduces logarithmic differentiation for complex exponents, making advanced calculus concepts accessible.

Takeaways
  • 📚 The video discusses mathematical concepts involving bases other than 'e', such as base 2 or base 7, and their derivatives and integrals.
  • 🔍 It starts with solving equations by using logarithms to isolate variables, demonstrating how to manipulate equations like 2^3x = 45 to find the value of 'x'.
  • 🧮 The logarithmic properties are used to simplify equations, showing that log_b(a^x) = x log_b(a), which is crucial for solving logarithmic equations.
  • 📈 The video explains how to convert logarithmic equations into exponential form, illustrating the process with an example equation involving base 5.
  • 📉 Derivatives of exponential functions are discussed, highlighting the formula d/dx(a^x) = a^x ln(a), which is different from the derivative of e^x.
  • 🔄 The integral of exponential functions is covered, showing how to reverse the derivative process to find the integral, using the formula ∫a^x dx = a^x/ln(a) + C.
  • 🌐 The concept of logarithmic differentiation is introduced, which is used when the variable is in both the exponent and the base of an expression.
  • 📘 The video emphasizes the importance of understanding the derivative of natural logarithms and how to apply it to different types of functions.
  • 📙 Change of base formula is mentioned, which is used to simplify logarithmic expressions and is crucial for understanding logarithmic functions.
  • 📚 The video provides a comprehensive overview of pre-calculus concepts, focusing on the application of logarithms and exponential functions in solving equations and finding derivatives and integrals.
Q & A

  • What is the main topic discussed in the video script?

    -The main topic discussed in the video script is dealing with exponential and logarithmic equations with bases other than 'e', such as base 2 or 7, and how to find derivatives and integrals of these functions.

  • How does the script suggest solving the equation 2^3x = 45?

    -The script suggests taking the natural logarithm of both sides of the equation to isolate 'x', then using properties of logarithms to bring down the coefficient of 'x' and finally dividing both sides by the natural logarithm of the base (2) to solve for 'x'.

  • What is the process for converting a logarithmic equation to an exponential form?

    -The process involves rewriting the logarithmic equation into an exponential form by taking the base of the equation to the power of what's on the other side of the equal sign.

  • What are some basic derivatives and integrals formulas mentioned in the script?

    -Some basic derivatives and integrals formulas mentioned include the derivative of natural 'e' to the power of 'u' being 'e' to the power of 'u' times 'u' prime, and the integral of 'e' to the power of 'u' being 'e' to the power of 'u' plus 'C'.

  • How does the script explain the derivative of a^u, where 'a' is any constant?

    -The script explains that the derivative of a^u is 'a' to the power of 'u' times the natural logarithm of 'a' times 'u' prime, which is different from the derivative of 'e' to the power of 'u' where the natural logarithm of 'e' is not included.

  • What is the method used in the script to find the derivative of y = 2^x^3?

    -The method used is to let 'u' equal 'x' cubed, find 'du/dx', and then apply the formula for the derivative of an exponential function, multiplying by the natural logarithm of the base and 'du/dx'.

  • What is the script's approach to dealing with logarithmic equations with different bases?

    -The script suggests using the change of base formula and turning everything into terms of natural logarithms, then applying the 'u' prime over 'u' derivative formula.

  • How does the script handle the integration of 2^x?

    -The script uses the integral formula for exponential functions, which involves dividing by the natural logarithm of the base and adding the constant of integration 'C'.

  • What is the process for finding the derivative of an expression where the variable is both in the exponent and the base?

    -The process involves using logarithmic differentiation, taking the natural logarithm of both sides, differentiating both sides, and then solving for the derivative of the original function.

  • What is the final example in the script about?

    -The final example is about finding the derivative of an expression where the variable is in both the exponent and the base, such as 'y = x^(x-3)', using logarithmic differentiation.

Outlines
00:00
🧮 Solving Equations with Logarithms

This paragraph introduces the concept of solving equations involving bases other than the common ones like 2 or 10. The focus is on using logarithms to isolate variables. An example is given where the equation 2^3x = 45 is solved using natural logarithms. The process involves taking the natural log of both sides, isolating the variable by dividing by the coefficient (3 in this case), and simplifying the expression to find the value of x. The explanation also touches on converting logarithmic equations into exponential form and emphasizes the importance of understanding the properties of logarithms.

05:03
📚 Derivatives and Integrals of Exponential and Logarithmic Functions

This paragraph delves into the derivatives and integrals of exponential and logarithmic functions. It starts with the basics, such as the derivative of e^u and the integral of e^u, and then moves on to more complex scenarios. The derivative of a^u (where a is any constant) is discussed, highlighting the need to multiply by the natural log of the base when a is not equal to e. The integral of exponential functions is also covered, with an example showing how to integrate 2^x by using the formula and substituting the appropriate values. The paragraph further explores the process of logarithmic differentiation, demonstrating how to find the derivative of a function where the variable is both in the exponent and the base, using the natural log and the product rule.

Mindmap
Keywords
💡Base
In mathematics, a 'base' refers to the number in an exponential expression which is raised to a power. In the context of the video, the base is not the common base 'e' but other numbers like 2 or 7, which are used to demonstrate how to handle equations and derivatives with different bases. For example, the video discusses how to deal with '2 to the power of x' and its derivative.
💡Derivative
The 'derivative' is a fundamental concept in calculus that represents the rate at which a function changes. It is the slope of the tangent line to the function at a given point. The video explains how to find derivatives of functions with different bases, such as 'a to the U', where 'a' is any constant, and uses the chain rule and natural logarithms.
💡Integral
An 'integral' is the reverse process of differentiation and is used to calculate the area under a curve or the accumulation of a quantity. The video covers the integration of exponential functions, such as '2 to the X', and demonstrates the process of reversing the derivative to find the original function.
💡Logarithm
A 'logarithm' is the inverse operation to exponentiation, used to solve equations involving unknown exponents. The video uses logarithms to simplify equations, such as taking the natural log of both sides to isolate the variable 'x' in an equation like '2^(3x) = 45'.
💡Natural Logarithm
The 'natural logarithm', often denoted as 'ln', is the logarithm to the base 'e', where 'e' is a mathematical constant approximately equal to 2.71828. The video script uses the natural logarithm to solve equations and as part of the process for finding derivatives and integrals of exponential functions.
💡Exponential Form
To express an equation in 'exponential form' means to write it in a way that clearly shows the base raised to a certain power. The video demonstrates converting a logarithmic equation into an exponential form, such as '5 to the power of Y equals x - 2', to make it easier to solve for 'x'.
💡Chain Rule
The 'chain rule' is a fundamental theorem in calculus for finding the derivative of a composite function. The video mentions the chain rule in the context of differentiating exponential functions where the base is not 'e', and an additional multiplication by the natural logarithm of the base is required.
💡Logarithmic Differentiation
Logarithmic differentiation is a technique used when the variable appears in both the base and the exponent of an expression. The video explains this process by taking the natural log of both sides of an equation and then differentiating, which simplifies the process of finding the derivative of complex functions.
💡Change of Base Formula
The 'change of base formula' is a mathematical tool used to convert the base of a logarithm to any other base. In the video, the formula is used to simplify the derivative of a logarithmic function by converting the base to 'e', which simplifies the differentiation process.
💡Product Rule
The 'product rule' is a rule in calculus for differentiating the product of two functions. The video script refers to the product rule when differentiating a function that involves a product of 'x - 3' and the natural log of 'x + 1'.
Highlights

Introduction to solving equations involving bases other than e, such as 2 or 7.

Explaining how to deal with derivatives and integrals of different bases.

Starting with solving equations where two equations are equal to each other.

Using logarithms to solve for x in equations.

Deriving the equation by bringing 3x down in front using logarithmic properties.

Solving for x by dividing both sides by 3 natural log of 2.

Converting the equation to a different representation using exponents.

Using exponential form to solve logarithmic equations.

Understanding the properties of logarithms and exponentials in solving equations.

Memorizing key derivatives and integrals formulas in calculus.

Derivative of a to the U where a is any constant.

Integral of exponential functions using the formula a to the U plus C.

Using logarithmic differentiation for functions with variables in both the exponent and the base.

Taking the natural log of both sides to simplify the differentiation process.

Applying the product rule in differentiation when dealing with a product of functions.

Finalizing the derivative by multiplying both sides by the original function.

Emphasizing the importance of understanding the process over memorizing formulas.

Transcripts

Browse More Related Video

Calculus 2 Lecture 6.3: Derivatives and Integrals of Exponential Functions

Ch. 4.3 Logarithmic Functions

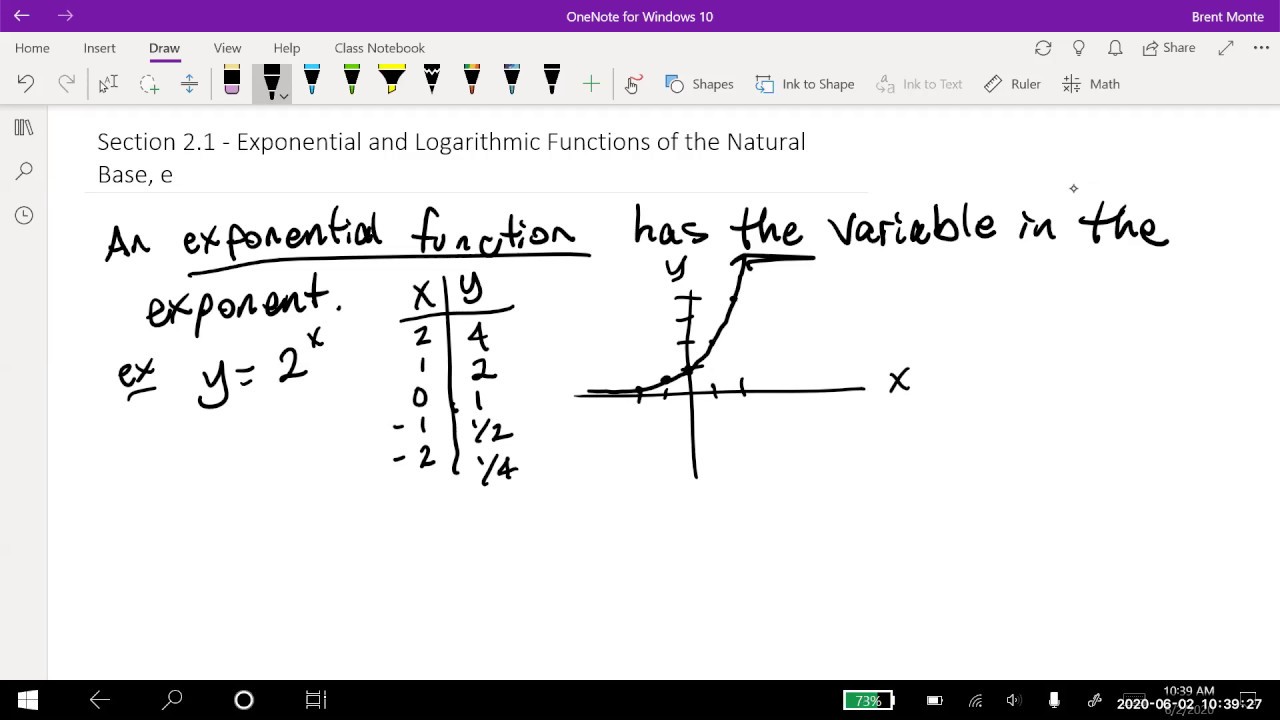
Math 11 - Section 2.1

Derivatives of Exponential Functions

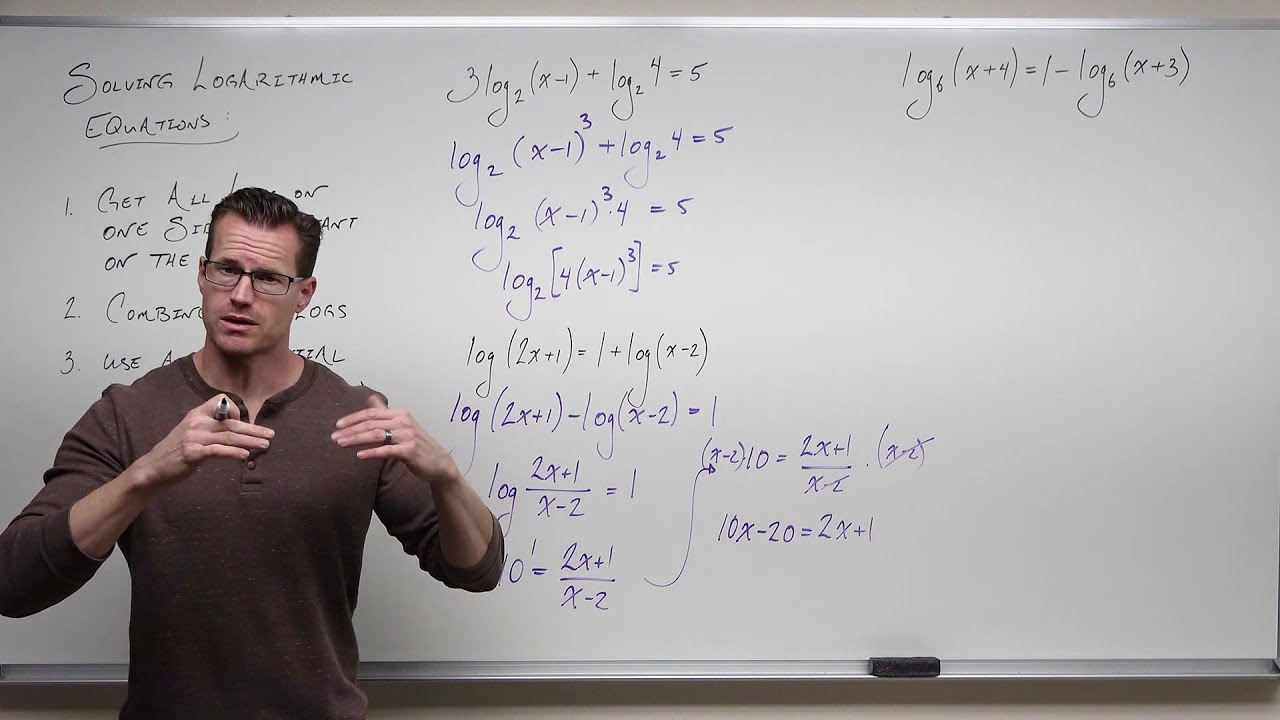
Solving Logarithmic Equations with Exponentials (Precalculus - College Algebra 63)

Solving Logarithmic Equations With Different Bases - Algebra 2 & Precalculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsBasesEquationsDerivativesIntegralsLogarithmsEducationalExponentialCalculusPre-Calculus