Ch. 4.3 Logarithmic Functions

Prof. Williams
27 Feb 202212:17
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script introduces logarithmic functions as the inverse of exponential functions, emphasizing their interplay. It explains the concept of natural logarithms and standard base 10 logarithms, highlighting the importance of understanding inverse functions. The script delves into logarithmic properties, the domain restrictions due to positive values only, and provides step-by-step examples of converting between exponential and logarithmic forms. It also illustrates solving logarithmic equations by transforming them into exponential form, showcasing problem-solving techniques for various logarithmic scenarios.

Takeaways
  • 🔍 Logarithmic functions are the inverse of exponential functions, with the base \( b \) of an exponential function \( b^x \) corresponding to the logarithm \( \log_b(x) \).
  • 📚 The natural logarithm, denoted as \( \ln(x) \), is the inverse of the natural exponential function with base \( e \).
  • 🔢 When no base is specified in a logarithmic expression, it is assumed to be base 10, reflecting the decimal number system based on powers of 10.
  • 📉 The domain of logarithmic functions is restricted to positive values, excluding zero, due to the nature of exponential functions which cannot yield negative or zero outputs.
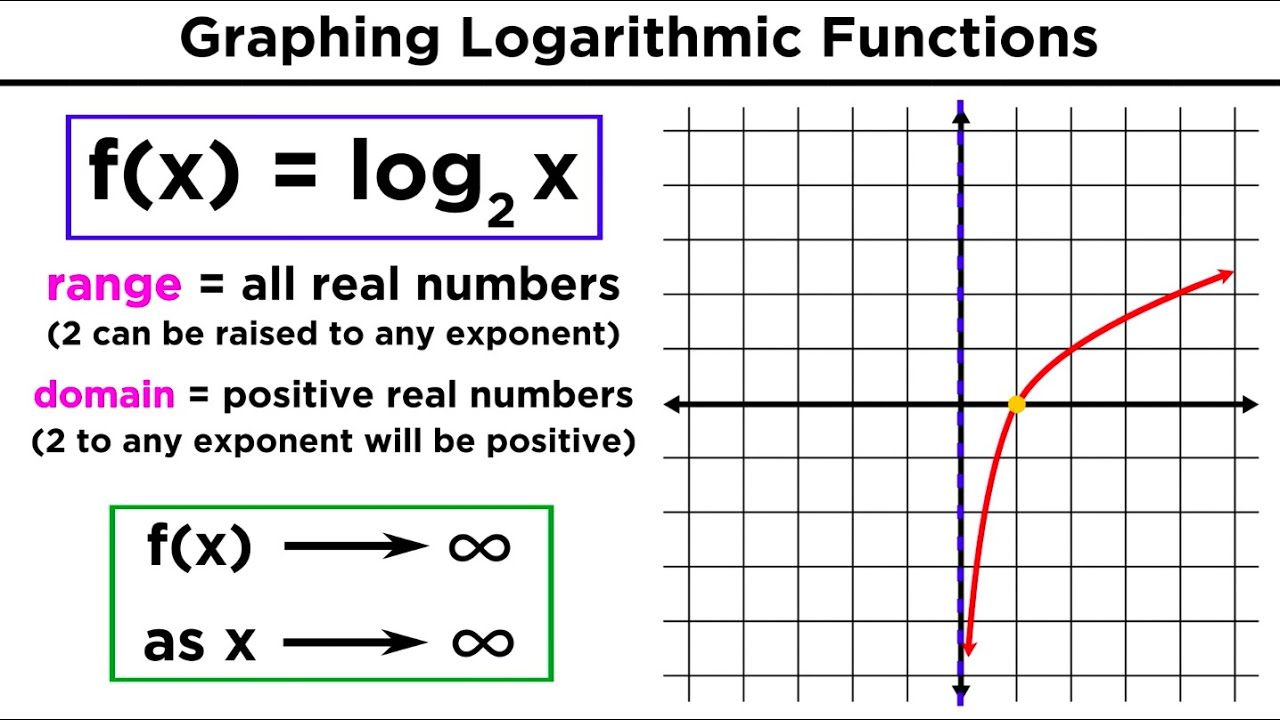
  • 📈 The graph of a logarithmic function, such as the base 10 logarithm, shows that \( \log(1) = 0 \) and the function approaches but never touches the x-axis as it extends to the right.
  • 🔑 Basic logarithmic properties include \( \log_b(1) = 0 \), \( \log_b(b) = 1 \), and \( \log_b(b^x) = x \), which are fundamental to understanding how to manipulate logarithmic expressions.
  • 🔄 To solve logarithmic equations, they are often converted into exponential form, which simplifies the process of finding the variable's value.
  • 📝 Examples given in the script demonstrate converting between logarithmic and exponential forms, such as solving \( \log_{12}(144) = 2 \) and \( \log(1000) = 3 \).
  • 🧩 Solving logarithmic equations involves recognizing the relationship between the input and output of the function and its inverse, using the 'out-in' rule for inverse functions.
  • 📖 The script suggests reviewing chapter 2.5 for a refresher on inverse functions if needed, emphasizing the importance of understanding this concept for grasping logarithms.
  • 🤔 The script also touches on the importance of understanding the base of logarithms, whether it's explicitly stated or implied as the standard base 10.
Q & A

  • What is the relationship between logarithmic functions and exponential functions?

    -Logarithmic functions are the inverse of exponential functions. If you have an exponential function with base 'b', the inverse function is 'log base b of x'.

  • What is a natural logarithm?

    -A natural logarithm is the inverse of the natural exponential function with base 'e'. It is written as 'ln(x)' instead of 'log base e of x'.

  • Why is the base 'e' considered the natural base for logarithms?

    -The base 'e' is considered natural because it has unique properties that make it particularly useful in mathematics, especially in calculus and continuous growth processes.

  • What is the standard base for logarithms when no base is specified?

    -When no base is specified for a logarithm, the standard base is 10, which is based on our decimal number system.

  • How do you remember the order of components in a logarithmic expression?

    -You can remember the order by starting at the base 'b', then moving clockwise to the input 'y', and finally to the output 'x'.

  • What is the domain of logarithmic functions?

    -The domain of logarithmic functions is all positive real numbers, excluding zero, because you cannot have a negative or zero exponent in an exponential function.

  • What is the significance of log base b of 1 being equal to 0?

    -Log base b of 1 equals 0 because any number raised to the power of 0 is 1, which is the definition of the logarithmic function at its base.

  • How do you convert a logarithmic equation to exponential form?

    -To convert a logarithmic equation to exponential form, you rewrite the equation so that the base of the logarithm is raised to the power of the variable, for example, 'log base b of y = x' becomes 'b^x = y'.

  • What is the relationship between the input and output of a logarithmic function and its inverse exponential function?

    -In a logarithmic function, the input is the exponent and the output is the result of the exponentiation. In its inverse exponential function, the roles are reversed: the input is the result of the exponentiation, and the output is the exponent.

  • How can you solve a logarithmic equation where the base is unknown?

    -To solve a logarithmic equation where the base is unknown, you can raise both sides of the equation to the reciprocal of the exponent to isolate the base, and then simplify if possible.

Outlines
00:00
📚 Introduction to Logarithmic Functions

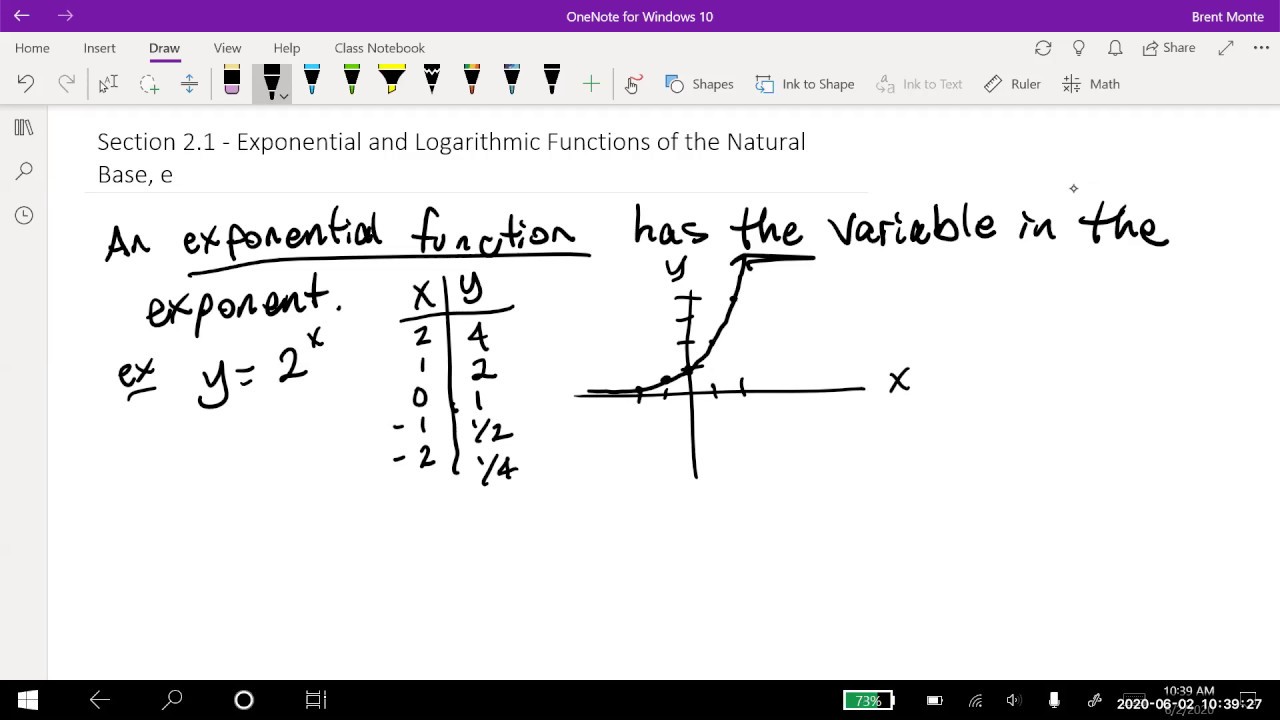
This paragraph introduces logarithmic functions as the inverse of exponential functions. The teacher explains how a logarithm with base 'b' can be represented as 'log base b of x' and vice versa. The concept of natural logarithms (ln) is introduced as the inverse of the natural exponential function with base 'e'. The standard base of 10 is explained as a result of our decimal system, and the teacher suggests reviewing inverse functions in chapter 2.5 for a better understanding. An example of converting an exponential equation to a logarithmic form is provided, illustrating the inverse relationship between the two.

05:01
📈 Basic Properties and Graph of Logarithms

The paragraph delves into the fundamental properties of logarithms, such as log base b of 1 being zero and log base b of b being one. The teacher discusses the domain restrictions of logarithmic functions, emphasizing that they can only accept positive values and cannot include zero or negative numbers due to the nature of exponential functions. A graphical representation of a basic logarithmic function is mentioned, and the importance of the log of 1 being zero is highlighted. The teacher also provides examples of converting logarithmic equations into exponential form to solve for variables.

10:01
🔍 Solving Logarithmic Equations

This section focuses on solving logarithmic equations by converting them into their exponential counterparts. The teacher demonstrates how to solve for 'x' in different logarithmic equations, such as 'log base 3 of 1/27 equals x' and 'natural log of x equals 5'. The process involves rewriting the logarithmic equation in exponential form and then solving for the variable. The teacher also addresses a situation where the base itself is the unknown variable, providing a method to solve for it by raising both sides of the equation to the reciprocal power.

Mindmap
Keywords
💡Logarithmic Functions
Logarithmic functions are mathematical functions that represent the inverse relationship to exponential functions. They are used to solve for the exponent in an equation where the result is known. In the video, logarithmic functions are introduced as the counterpart to natural exponential functions, with the script explaining that if the exponential function is 'b to the x', then the inverse, or logarithmic function, is 'log base b of x'. The concept is central to the video's theme of exploring the inverse relationship between exponential and logarithmic forms.
💡Exponential Functions
Exponential functions describe a mathematical relationship where a constant base is raised to a variable exponent. They are fundamental in various fields, including finance and science. The script mentions that exponential functions are inverse to logarithmic functions, with the example given as 'b to the x' being the inverse of 'log base b of x', highlighting their reciprocal nature in mathematical operations.
💡Inverse Functions
Inverse functions are a pair of functions where applying one and then the other returns the original value. In the context of the video, the concept is used to explain how logarithmic functions are the inverse of exponential functions. The script suggests revisiting chapter 2.5 for a refresher on inverse functions, emphasizing their importance in understanding the relationship between exponential and logarithmic forms.
💡Natural Exponential Function
The natural exponential function refers to the exponential function with the base 'e', which is approximately equal to 2.71828. It is widely used in mathematics due to its unique properties. The video script introduces 'e' as the base for the natural exponential function and discusses its inverse, the natural logarithm, denoted as 'ln', which is a key concept in the study of logarithms.
💡Natural Logarithm
The natural logarithm, denoted as 'ln', is the logarithm to the base 'e'. It is a specific type of logarithm that is commonly used in calculus and other mathematical fields. The script explains that 'ln' is the inverse of the natural exponential function and uses the term to illustrate the conversion between logarithmic and exponential forms.
💡Standard Base
The standard base, typically denoted as base 10, is the default base used in common logarithms when no other base is specified. The script explains that our number system is based on tens, which is why base 10 is used as the standard. It is used in the context of the video to explain the default base when 'log of x' is written without a specified base.
💡Domain
In mathematics, the domain of a function is the set of all possible input values (x-values) for which the function is defined. The script clarifies that the domain of logarithmic functions is from zero to infinity, excluding zero, because logarithms cannot accept negative numbers or zero as inputs, as they would not yield real number outputs.
💡Logarithmic Properties
Logarithmic properties are the rules that govern the behavior of logarithms in mathematical expressions. The script mentions that the basic properties of logarithms, such as 'log base b of 1 equals 0' and 'log base b of b equals 1', will be covered in more detail in subsequent sections, but provides a foundational understanding of these properties within the context of the video.
💡Graph of Logarithm
The graph of a logarithmic function is a visual representation of the function's behavior. The script revisits the graph of a basic base 10 logarithm, noting that it passes through the point (1, 0) and has a vertical asymptote at x = 0, which illustrates the domain restriction of logarithmic functions.
💡Solving Logarithmic Equations
Solving logarithmic equations involves finding the value of the variable that makes the equation true. The script provides examples of converting logarithmic equations into exponential form to solve for the variable, such as converting 'log base 3 of 1/27 equals x' into '3 to the x equals 1/27', demonstrating the method to find the solution for x.
Highlights

Logarithmic functions are the inverse of natural exponential functions.

The inverse function of b to the power of x is log base b of x.

Natural logarithm, ln, is the inverse of the natural exponential function with base e.

If no base is specified in a logarithm, the standard base of 10 is assumed.

The standard base of 10 is used due to our decimal number system based on tens.

The process of converting between logarithmic and exponential forms is demonstrated with examples.

The logarithm of 1 to any base is always 0, reflecting the fundamental property of exponents.

The logarithm of a base b is always 1, as it represents the identity of the function.

The domain of logarithmic functions is restricted to positive values, excluding zero.

The graph of a basic base 10 logarithm function is reviewed, emphasizing key values.

The concept of converting logarithmic equations to exponential form for solving is introduced.

An example of solving log base 3 of 1/27 is provided, demonstrating the conversion process.

The natural logarithm of x equals 5 is solved by converting to exponential form e to the power of 5.

An example where the base is unknown is solved by raising both sides to the reciprocal power.

The simplification of an equation involving fractional exponents is shown to find a more elegant solution.

The importance of understanding inverse functions for solving logarithmic and exponential problems is emphasized.

The process of going back and forth between logarithmic and exponential forms is essential for problem-solving.

Transcripts

Browse More Related Video

Business Calculus -- Math 1329 -- Section 4.2 -- Logarithmic Functions

Logarithms Part 1: Evaluation of Logs and Graphing Logarithmic Functions

Solving Complex Logarithmic Equations

Math 11 - Section 2.1

Logarithms Explained Rules & Properties, Condense, Expand, Graphing & Solving Equations Introduction

Bases other than e

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Logarithmic FunctionsExponential FunctionsInverse FunctionsMathematics EducationNatural LogarithmBase ConversionLog PropertiesEducational ContentMath TutorialAlgebra Concepts