Calculus 2 Lecture 6.3: Derivatives and Integrals of Exponential Functions
TLDRThe video script delves into the world of exponential functions, focusing on the constant 'e' and its unique properties. It introduces 'e' as the base of natural logarithms, highlighting its irrational nature similar to Pi. The instructor explains the mathematical definition of 'e' and its relationship with natural logarithms, using integrals and the intermediate value theorem. The script covers the properties of 'e' and its graph, including its domain, range, continuity, and concavity. It also explores solving exponential and logarithmic equations using algebraic manipulations and the fundamental properties of 'e'. The session progresses to discuss the derivatives and integrals of exponential functions, emphasizing the simplicity of their calculations and providing examples to solidify understanding. The instructor prepares students for more complex topics like general exponential and logarithmic functions with varying bases.
Takeaways
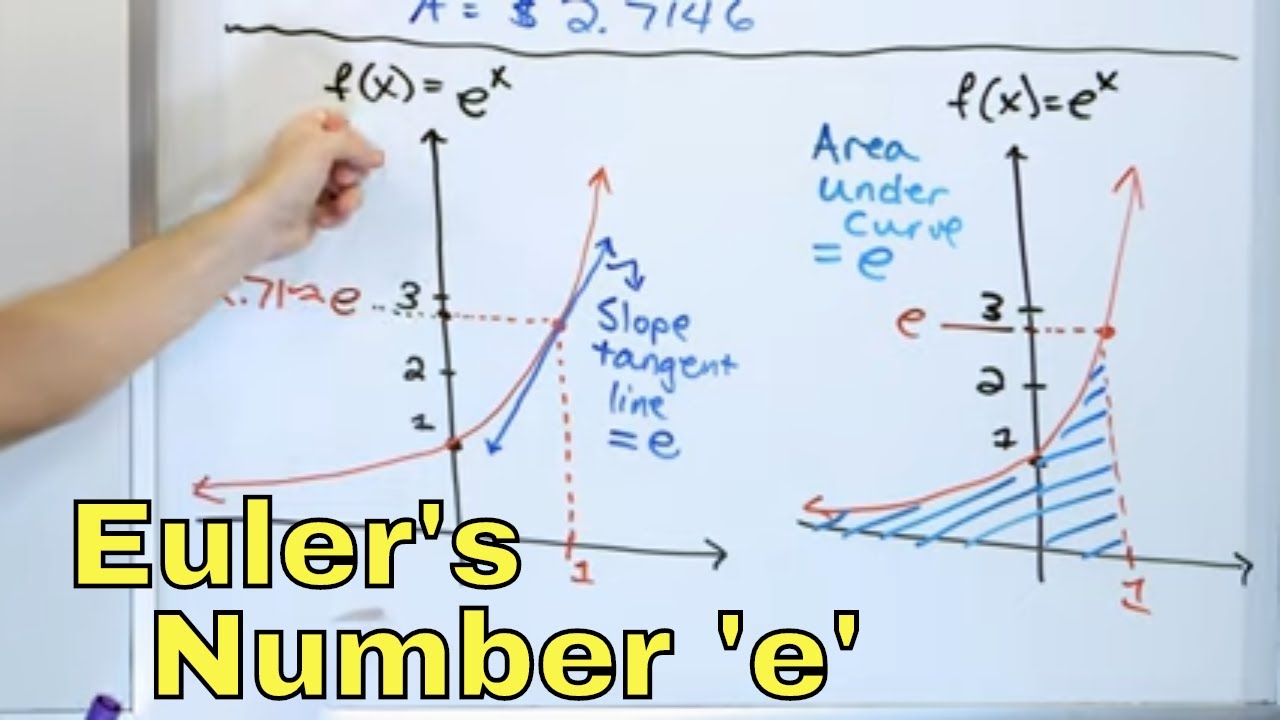
- 📚 The number e is introduced as the base of natural logarithm, an irrational number similar to Pi, and is approximately equal to 2.71828.
- 🔍 e is discovered by Leonard Euler, and it is also known as the Oiler number, named after him but spelled differently in German (euler -> euler).
- 🌟 The mathematical definition of e is given by the integral of 1/x dx from 1 to x, where e^x is the inverse of the natural logarithm function.
- 📉 The natural logarithm function, ln(x), is continuous and has a range from negative infinity to positive infinity, with the intermediate value theorem ensuring the existence of e.
- 🔢 Properties of e and ln(x) are discussed, such as ln(e^x) = x and e^(ln(x)) = x, which are useful for solving exponential and logarithmic equations.
- 📌 Examples of solving equations involving e and ln(x) are provided, demonstrating the application of the properties mentioned earlier.
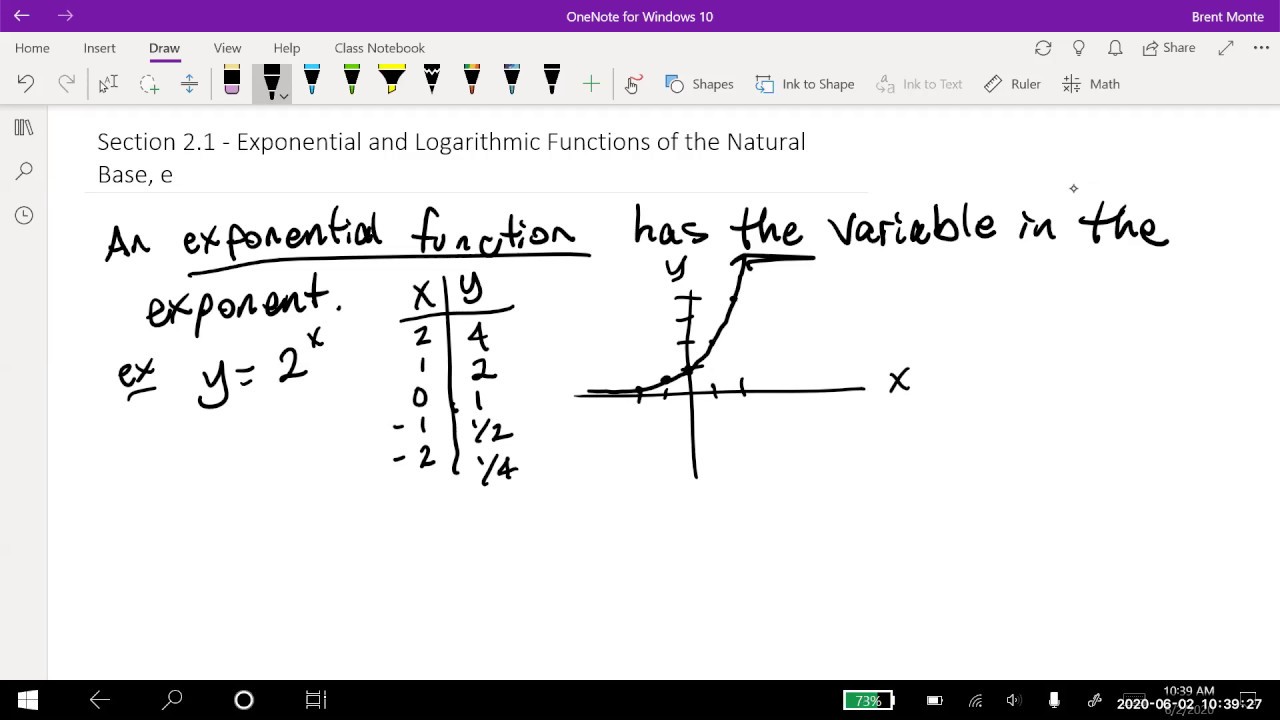
- 📈 The domain and range of the exponential function e^x are discussed, with the domain being all real numbers and the range being all positive real numbers.
- 📚 The function e^x is continuous everywhere and is always concave up, with limits at infinity and negative infinity being approached differently.
- 🧩 The concept of logarithmic differentiation is briefly introduced, which is a method used to find derivatives of functions involving products, quotients, and compositions.
- 🔑 The derivative of e^x is e^x itself, a simple yet powerful rule that is key to calculus, and it is derived using logarithmic differentiation.
Q & A
What is the mathematical constant 'e'?
-The constant 'e' is an important mathematical number, approximately equal to 2.71828. It is an irrational number, which means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating. It is often referred to as Euler's number and is the base of the natural logarithm.
Who is credited with discovering the number 'e'?
-Leonhard Euler is credited with discovering the number 'e'. His surname 'Euler' is pronounced 'oiler' in German, which is where the 'e' in 'e' comes from, although it is spelled differently in English.
What is the definition of 'e' in terms of natural logarithm?
-The number 'e' is defined such that the natural logarithm of 'e' (Ln(e)) equals 1. Mathematically, e is the number for which the area under the curve of 1/t from 1 to e is equal to 1.
How is the number 'e' related to exponential functions?
-The number 'e' is the base of the natural exponential function. It is used as the base in exponential functions because it has unique properties that make it the natural choice for modeling growth and decay processes in various fields such as mathematics, physics, and engineering.
What are some properties of logarithms and exponentials involving 'e'?
-There are several key properties involving 'e' and logarithms: 1) Ln(e^x) = x, meaning the natural logarithm of e raised to the power of x is equal to x. 2) e^(Ln(x)) = x, indicating that raising e to the power of the natural logarithm of x yields x.
How can the properties of 'e' be used to solve exponential equations?
-The properties of 'e' can be used to simplify and solve exponential equations by allowing you to cancel out the exponential and logarithmic parts when they appear next to each other in an equation, making it easier to isolate and solve for the variable.
What is the domain and range of the exponential function e^x?
-The domain of the exponential function e^x is all real numbers, which means you can input any real number into the function. The range of e^x is all positive real numbers (0 to infinity), as the function never touches or crosses the x-axis and only produces positive outputs.
Is the exponential function e^x continuous?
-Yes, the exponential function e^x is continuous for all real numbers. This means that there are no gaps or jumps in the graph of the function, and it can be represented by a smooth, unbroken curve.
What is the limit of e^x as x approaches positive infinity?
-The limit of e^x as x approaches positive infinity is also positive infinity. This means that as x becomes larger and larger in the positive direction, the value of e^x also increases without bound.
What is the limit of e^x as x approaches negative infinity?
-The limit of e^x as x approaches negative infinity is 0. This means that as x becomes more and more negative, the value of e^x gets closer and closer to 0, approaching but never actually reaching zero.
How can you find the derivative of a function involving e^x?
-The derivative of a function involving e^x can be found using the chain rule if the exponent is a function of x. If the function is simply e^x, then its derivative is e^x itself. If the function is e^(u(x)), where u(x) is another function of x, then the derivative is e^(u(x)) times the derivative of u(x), or du/dx.
What is the integral of e^x with respect to x?
-The integral of e^x with respect to x is simply e^x plus the constant of integration, C. This is because e^x is its own antiderivative, and the integral of a function that is its own derivative will result in the function itself plus a constant.
What is the process of substitution used in calculus for integrals?
-The process of substitution in calculus for integrals involves replacing a part of the integrand with a new variable, which simplifies the integral to a form that is easier to compute. It is often used when the integral does not fit the standard integration formulas and can transform the integral into one that does.
How do you determine the appropriate substitution for an integral?
-To determine the appropriate substitution for an integral, you need to identify a part of the integrand that, when substituted with a new variable, will simplify the integral and make it fit a standard integration formula. This often involves recognizing a pattern or a function within the integral that can be replaced to eliminate complex expressions.
What is the derivative of e^(x^2)?
-The derivative of e^(x^2) is found using the chain rule. The derivative is 2x * e^(x^2), where the derivative of the inner function x^2 is 2x, and the derivative of e^u (where u is a function of x) is e^u.
Can you integrate the product of e^x and another function without substitution?
-No, you cannot directly integrate the product of e^x and another function without using substitution or another integration technique unless the product fits a known integration formula.
What is the integral of e^x divided by x?
-The integral of e^x divided by x is not a standard integral and requires substitution or another integration technique to solve. One common approach is to use integration by parts or a suitable substitution to simplify the integral.
How do you find the integral of a function that includes both e^x and a polynomial?
-To find the integral of a function that includes both e^x and a polynomial, you can use substitution to simplify the polynomial part of the function, making it easier to integrate. After the substitution, you can then integrate e^x, which is a standard integral.
What is the integral of e^x multiplied by a constant?
-The integral of e^x multiplied by a constant, say 'c', is simply c * e^x plus the constant of integration, C. This is because the derivative of e^x is e^x, and multiplying by a constant does not change the antiderivative.
What is the integral of e^(2x)?
-The integral of e^(2x) can be found using substitution. If you let u = 2x, then du = 2 dx, or dx = du/2. The integral becomes 1/2 * integral of e^u du, which simplifies to 1/2 * e^u + C, and substituting back for u gives 1/2 * e^(2x) + C.
How do you integrate a function involving e^x when the exponent is a quadratic expression?
-When the exponent is a quadratic expression, you can use substitution to simplify the integral. For example, if the integral is e^(x^2), you might let u = x^2, then du = 2x dx, and the integral becomes 1/2 * integral of e^u du, which is a standard integral.
What is the integral of e^x divided by a quadratic expression?
-The integral of e^x divided by a quadratic expression requires a substitution that simplifies the quadratic expression. For example, if the integral is e^x / (x^2 + 1), you might let u = x + 1/x, then du = (1 - 1/x^2) dx, and the integral can be simplified and solved using known integration techniques.
What is the integral of e^x multiplied by x?
-The integral of e^x multiplied by x is found using substitution. If you let u = x, then du = dx, and the integral can be solved.
Outlines
📚 Introduction to Exponential Functions and the Number e
The speaker begins by introducing the topic of exponential functions and the special number e, emphasizing its significance in mathematics and natural occurrences. They explain that e, similar to Pi, is an irrational number with a non-repeating decimal expansion approximately equal to 2.71828. The number e is associated with continuous growth processes and is derived from the work of Leonard Euler, a prominent mathematician. The talk also covers the mathematical definition of e as the unique number for which the natural logarithm equals one, and touches on the intermediate value theorem to illustrate the existence of e within the natural logarithm function.
🔍 Properties and Applications of Exponential Functions and Logarithms
This paragraph delves into the properties of exponential functions and logarithms, particularly focusing on their use in solving equations involving e or natural logarithms (Ln). The presenter explains the relationship between exponentials and logarithms, highlighting the key property that e^x * ln(e^x) = x. They also demonstrate how to simplify expressions involving e and ln by 'canceling each other out' and provide proofs for these properties. The speaker then guides through solving sample exponential and logarithmic equations, emphasizing the importance of applying properties correctly to find solutions.
📘 Algebraic Manipulation and Solving Exponential Equations
The speaker continues with an algebraic exploration of exponential equations, discussing strategies for isolating the base e and applying natural logarithms to both sides of an equation. They provide a step-by-step walkthrough for solving equations like e^(5x - 1) = 23 and emphasize the importance of checking solutions against the domain of the natural logarithm function, which requires arguments to be greater than zero. The paragraph also covers techniques for dealing with trinomials and the potential to transform them into quadratic equations through substitution.
📘 Continuation of Algebraic Techniques and Exponential Properties
Building on the previous discussion, the speaker further elaborates on algebraic techniques applicable to exponential equations. They introduce the idea of combining natural logarithms and using properties of exponents to simplify equations. The paragraph also touches on the domain and range of the exponential function e^x, highlighting that it is continuous across its entire domain and has a range from positive infinity down to values approaching zero but never reaching it. The speaker also discusses the concavity of the exponential function and its implications.
📘 Limits and Continuity of Exponential Functions
The focus shifts to the limits of exponential functions as x approaches both positive and negative infinity. The speaker explains that the function e^x tends to infinity as x becomes large and positive, and approaches zero as x becomes large and negative, though never actually reaching zero. They also discuss the continuity and concavity of e^x, emphasizing its concave-up shape across its entire domain. Additionally, the speaker introduces the concept of limits in relation to the natural logarithm function, noting its behavior as x approaches zero from the right.
📘 Applications of Exponential Functions in Calculus
The speaker introduces the concept of derivatives of exponential functions, specifically the derivative of e^x, which is e^x itself. They provide a proof using logarithmic differentiation, showing that the derivative of y = e^x simplifies to y = e^x. The paragraph also covers the application of the chain rule when differentiating exponential functions where the exponent is a function of x, emphasizing the importance of multiplying the derivative of the inner function by the derivative of the outer function.
📘 Advanced Derivatives and Chain Rule Applications
This section delves deeper into the application of the chain rule for derivatives of exponential functions. The speaker provides examples of how to handle more complex expressions involving e^x raised to powers or multiplied by other functions. They emphasize the importance of correctly applying the chain rule and the product rule when differentiating such expressions. The speaker also illustrates how to simplify derivatives by factoring out common terms and using substitution techniques.
📘 Derivatives of Exponential Functions with Complex Expressions
The speaker presents a challenging problem involving the derivative of a complex expression that includes both exponential and logarithmic components. They guide the audience through the process of applying the chain rule and the product rule to break down the expression into manageable parts. The explanation includes restating the original function in a form that simplifies the differentiation process and emphasizes the importance of recognizing when to apply these differentiation rules.
📘 Integration of Exponential Functions
Transitioning to integration, the speaker explains that the integral of e^x is straightforward, resulting in e^x plus a constant of integration (+C). They introduce the concept of substitution for integrating more complex exponential expressions, such as e^(2x), and demonstrate how to set up and execute the substitution to simplify the integral. The paragraph emphasizes the importance of recognizing when a substitution is necessary and how to apply it correctly to find the integral of an exponential function.
📘 Advanced Integration Techniques and Substitution
The speaker continues to explore integration techniques, specifically focusing on substitution for integrals involving exponential functions with more complex exponents. They provide examples of how to identify suitable substitutions, such as setting u to the exponent of e in the integral, and demonstrate the process of changing the integral into a form that fits the integration table. The paragraph also discusses the importance of converting the integral back to the original variable after performing the substitution.
📘 Complex Integration and Derivation of Exponential Functions
In this section, the speaker tackles more complex integrals involving exponential functions and demonstrates how to apply substitution to transform them into a solvable form. They provide detailed examples, including integrals with secant and exponential components, and explain how to simplify these expressions using appropriate substitutions. The speaker also emphasizes the importance of re-substituting to revert back to the original variable and the utility of absolute values in certain integrals.
📚 General Exponential and Logarithmic Functions
The speaker concludes the session by预告即将到来的课程内容,讨论一般指数函数和对数函数。他们提到,除了特定的底数e,他们还将探讨具有任何其他常数底数或甚至x的函数的指数和对数函数。这为下一部分课程内容提供了一个自然的过渡,并表明了对更广泛的指数和对数概念的探索。
Mindmap
Keywords
💡Exponential Functions
💡Natural Logarithm
💡Irrational Number
💡Euler's Number
💡Logarithmic Equations
💡Derivatives
💡Chain Rule
💡Continuity
💡Concavity
💡Limits
💡Integration
Highlights
Introduction to exponential functions and defining the base of natural logarithm, the number e.
Historical background of the number e, named after Leonard Euler.
Irrationality and infinite nature of the number e, similar to Pi.
The mathematical definition of e as the base of natural logarithm where ln(e) equals 1.
Explanation of the integral definition of natural logarithm and its relation to the area under a curve.
Existence of the number e proven by the intermediate value theorem and properties of continuous functions.
Properties of exponential and logarithmic functions that help solve equations.
Solving exponential and logarithmic equations using algebraic manipulation.
Derivative of exponential functions with base e, which is a fundamental concept in calculus.
Proof of the derivative of e^x being e^x using logarithmic differentiation.
Application of the chain rule in derivatives of exponential functions.
Integration of exponential functions and the use of substitution method.
Substitution technique in integral calculus to simplify complex integrals.
General exponential functions and logarithmic functions with any base.
Importance of understanding the domain and range of exponential functions.
Limit concepts and their application in exponential and logarithmic functions.
Continuity and concavity of exponential functions with examples.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: