2.1 Significant Figures | High School Chemistry

Chad's Prep

31 Aug 202014:36

EducationalLearning

32 Likes 10 Comments

TLDRThis high school chemistry lesson focuses on significant figures, a crucial concept in measurement. The instructor explains the importance of understanding significant figures through a relatable example involving distance measurements and emphasizes their relevance in fields like engineering. Four rules for determining significant zeros are outlined, with examples provided to clarify when zeros are significant and when they are not. The lesson also covers the impact of significant figures on mathematical operations like multiplication, division, addition, and subtraction, highlighting the different rules for each. The instructor encourages students to apply these concepts in lab reports and exams, noting that while not always tested, they are essential for accurate scientific communication.

Takeaways

📚 The script is part of a high school chemistry lesson series focused on the concept of significant figures.
🔍 Significant figures are crucial for determining the accuracy of measurements and calculations in chemistry.
👋 The video introduces four main rules for determining when zeros are significant in a number.
🌟 Zeros at the beginning of a number are never significant, regardless of the context.
🌈 Zeros between significant digits are always significant, indicating precision in measurement.
❗ Zeros at the end of a number can be significant depending on their position relative to the decimal point.
🧮 The rules for significant figures change depending on the mathematical operation being performed, with different rules for multiplication/division and addition/subtraction.
📉 In multiplication and division, the result's number of significant figures is determined by the number with the fewest significant figures.
📈 For addition and subtraction, the result's precision is determined by the least specific decimal place among the numbers involved.
🛠️ The importance of significant figures is emphasized for lab reports and exams, where they are often a focus of assessment.
📝 The script suggests that while significant figures are important for lab reports, they may not always be the focus in other parts of a chemistry course.
🔗 The instructor promotes a premium course for additional practice and study materials related to the lesson.

Q & A

What is the main topic of the first lesson in the high school chemistry playlist?
-The main topic of the first lesson is significant figures.
Why are significant figures important in measurements?
-Significant figures are important because they indicate the precision of a measurement. They help in understanding how accurately a number is known and are crucial in fields like engineering where precision is critical for safety and functionality.
What is the role of zeros in determining significant figures?
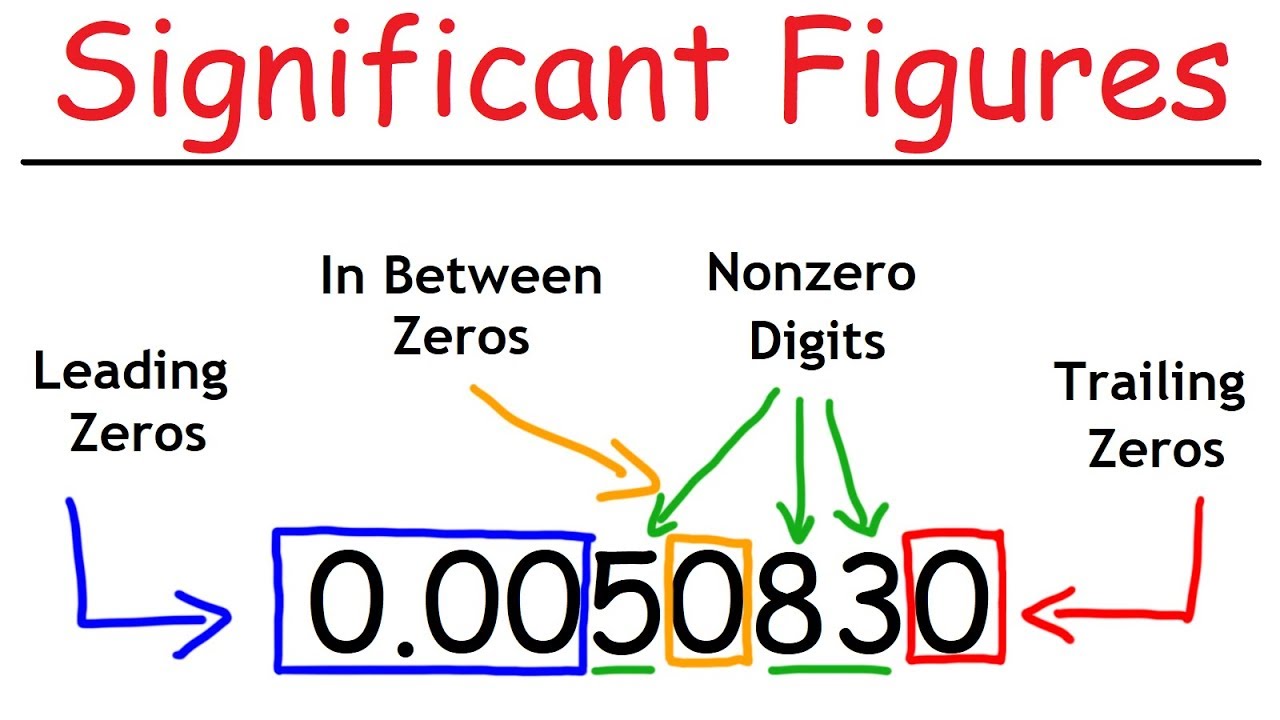
-Zeros play a crucial role in determining significant figures. They can be significant or not depending on their position in a number. Zeros at the beginning of a number are never significant, zeros in the middle of a number are always significant, and zeros at the end of a number can be significant if they are to the right of the decimal point.
What are the four rules for determining when zeros are significant in a number?
-The four rules are: 1) Zeros at the beginning of a number are never significant. 2) Zeros at the end of a number to the left of the decimal point are not significant. 3) Zeros at the end of a number to the right of the decimal point are significant. 4) Zeros in the middle of a number are always significant.
How does the precision of a measurement affect the result when adding two numbers?
-The result of adding two numbers can only be as precise as the least precise number involved in the calculation. If one number is known to a certain decimal place and the other is only known to a less precise place, the result must be rounded to the least precise place.
What is the rule for significant figures when performing multiplication and division?
-When performing multiplication and division, the result should have the same number of significant figures as the number with the fewest significant figures in the calculation.
How does the rule for significant figures differ when performing addition and subtraction compared to multiplication and division?
-In addition and subtraction, the result should be rounded to the least specific decimal place of the numbers involved, rather than matching the number with the fewest significant figures as in multiplication and division.
Why might it be beneficial to use scientific notation when dealing with significant figures?
-Scientific notation can be beneficial when dealing with very large or very small numbers, as it simplifies the process of determining significant figures and avoids confusion with zeros that are not significant.
What is the significance of expressing calculations in the proper number of significant figures on lab reports?
-Expressing calculations in the proper number of significant figures on lab reports is important because it accurately reflects the precision of the measurements and the reliability of the results.
How can a good calculator help in determining significant figures in calculations?
-A good calculator can help in determining significant figures by performing precise calculations and allowing users to easily round results to the appropriate number of significant figures.

Outlines

00:00

🔍 Introduction to Significant Figures in Chemistry

This paragraph introduces the concept of significant figures in the context of a high school chemistry lesson. The instructor explains the importance of significant figures in measurement and how they affect the accuracy of results. The lesson will cover four main rules regarding significant figures, starting with the significance of zeros in numbers. The instructor uses a relatable example involving distances to illustrate the concept, emphasizing the practical implications of significant figures in real-world applications like engineering.

05:01

📚 Rules for Determining Significant Figures

The second paragraph delves into the four rules for identifying significant figures, focusing on the role of zeros in numbers. The instructor explains that zeros at the beginning of a number are not significant, while zeros between significant digits are always significant. The rules for zeros at the end of a number are more complex, depending on their position relative to the decimal point. The instructor also discusses the implications of these rules in mathematical operations, particularly multiplication and division, where the number of significant figures in the result is determined by the number with the fewest significant figures in the operation.

10:02

📉 Applying Significant Figures to Mathematical Operations

In this paragraph, the instructor discusses the application of significant figures to addition and subtraction, which is less common in chemistry but important to understand. The rule for these operations is based on the least specific decimal place rather than the number with the least significant figures. The instructor provides examples of calculations and how to round the results to the correct number of significant figures. The paragraph also touches on the importance of significant figures in lab reports and exams, and the instructor suggests that students invest in a good calculator for accurate calculations.

📝 Conclusion and Additional Resources

The final paragraph wraps up the lesson on significant figures, emphasizing their importance in lab reports and exams. The instructor clarifies that while significant figures may not always be tested in the rest of the chemistry course, they are crucial for accurate reporting. The instructor also provides a word of advice regarding the use of scientific notation for easier handling of numbers with many zeros, which will be covered in a subsequent lesson. The paragraph concludes with an invitation for students to check out additional resources and courses for further practice and understanding of the topic.

Mindmap

Keywords

💡Significant Figures

Significant figures refer to the digits in a number that carry meaning contributing to its precision. In the video, the concept is crucial as it determines the accuracy of measurements and calculations in chemistry. For example, the distinction between '3000 miles' and '3043.216 miles' highlights the importance of knowing how many digits in a measurement are significant.

💡Scientific Notation

Scientific notation is a way of expressing very large or very small numbers using powers of ten. It is mentioned in the script as a topic to be covered in a future lesson, suggesting its relevance in handling numbers with many significant figures, especially in chemistry.

💡Accuracy and Precision

Accuracy refers to how close a measurement is to the true value, while precision indicates the level of consistency in repeated measurements. The video script discusses these concepts in the context of measurement, emphasizing their importance in scientific experiments and calculations.

💡Units and Conversions

Units and conversions are essential in chemistry for measuring and comparing different quantities. The script mentions a lesson on this topic, indicating its importance in understanding how different units of measurement relate to each other and how to convert between them accurately.

💡Zeros

The role of zeros in significant figures is a central theme in the video. The script explains that zeros can either be significant or not, depending on their position in a number. For instance, zeros at the end of a number to the left of the decimal point are not significant, while those to the right are.

💡Measurement

Measurement is the process of determining the size, amount, or degree of something. The video script uses the example of measuring distances to illustrate the concept of significant figures and how they affect the precision of measurements.

💡Engineering

Engineering is mentioned in the context of applying the principles of science and mathematics to design and build structures like buildings and bridges. The script highlights the importance of knowing the significant figures in calculations to ensure the safety and stability of these structures.

💡Multiplication and Division

The script discusses the rules for significant figures in multiplication and division, stating that the result should have the same number of significant figures as the number with the fewest significant figures in the calculation. This is crucial for maintaining the accuracy of scientific calculations.

💡Addition and Subtraction

The rules for significant figures in addition and subtraction are different from those in multiplication and division. The video explains that the result should be rounded to the least specific decimal place, which is determined by the number with the least precision in the calculation.

💡Lab Reports

Lab reports are mentioned as a context where significant figures are always important. The script suggests that students should always express calculations in the proper number of significant figures when reporting results in a lab setting.

💡Decimal

The decimal point is crucial in determining the significance of zeros in a number. The script explains that zeros to the right of the decimal point in a number are significant, while those to the left are not, unless they are between significant figures.

Highlights

Introduction to significant figures in the context of high school chemistry.

Explanation of the importance of significant figures in measurement.

Upcoming lessons on scientific notation, accuracy, precision, and units and conversions.

The challenge of determining the significance of zeros in numbers.

Illustration of significant figures using the example of Bob's aunt and uncle's distances.

The concept that significant figures affect the accuracy of calculated results.

The significance of accurate measurements in engineering and construction.

Four rules for determining when zeros are significant in numbers.

Rule one: Zeros at the beginning of a number are not significant.

Rule four: Zeros between significant figures are always significant.

Rule two and three: The significance of trailing zeros depends on their position relative to the decimal point.

The use of scientific notation to simplify the handling of significant figures.

Different rules for significant figures in multiplication/division versus addition/subtraction.

How to apply the rule for multiplication and division to determine the significant figures of a result.

How to apply the rule for addition and subtraction to determine the significant figures of a result.

The importance of expressing calculations with the correct number of significant figures in lab reports and exams.

The potential use of a scientific calculator for handling significant figures in calculations.

Transcripts

Browse More Related Video

Significant Figures Step by Step | How to Pass Chemistry

What are Significant Figures, Precision & Accuracy in Chemistry & Physics?

Rounding and Order of Operations Used in Significant Figures

College Physics 1: Lecture 3 - Significant Figures and Scientific Notation

Significant Figures - A Fast Review!

Measurement and Significant Figures