14 - What is Euler's Number 'e', Ln(x) - Natural Log & e^x Functions?
TLDRThis lesson delves into Euler's number 'e', exploring its origin from compound interest calculations and its significance in mathematics. It highlights 'e' as a fundamental constant, akin to pi, and discusses its role in exponential functions and natural logarithms. The video also touches on the unique properties of the exponential function e^x and introduces Euler's formula, showcasing the beauty of mathematical relationships.
Takeaways
- 📚 The lesson introduces Euler's number (e), a fundamental concept in mathematics, which is approximately 2.71828 and is an irrational number like pi.
- 🔍 Euler's number is derived from the study of exponential growth, particularly in the context of compound interest calculations.
- 🌐 Euler's number is as important as pi in mathematics, appearing frequently in advanced mathematics, engineering, and science.
- 💡 The natural logarithm (ln) and the natural exponential function (e^x) are closely related, with e being the base of the natural logarithm.
- 🧮 The number e is approached by continuously increasing the frequency of compounding interest in a formula, eventually leading to the limit definition of e as the compounding periods approach infinity.
- 📈 The graph of the exponential function e^x is unique in that the slope of the tangent line at any point on the curve is equal to the value of the function at that point.
- 📉 The area under the curve of e^x from negative infinity to any point x is equal to the value of the function at that point, demonstrating the special properties of this exponential function.
- 🌟 Euler's number is part of Euler's formula, which is considered one of the most beautiful equations in mathematics, linking e, i, pi, 1, and 0.
- 💻 The exact value of e is calculated using methods from calculus, which are beyond the scope of basic mathematics but are essential for understanding the limit definition of e.
- 📚 The lesson emphasizes the importance of understanding where mathematical concepts like e come from, setting the stage for further studies in calculus and advanced mathematics.
Q & A
What is Euler's number?
-Euler's number, commonly denoted as 'e', is a mathematical constant approximately equal to 2.71828. It is an irrational number, meaning its decimal representation goes on forever without repeating.
Why is Euler's number important in mathematics?
-Euler's number is crucial in mathematics because it frequently appears in calculations involving exponential growth and decay, compound interest, and logarithms. It is also fundamental in advanced mathematics, including calculus, where it is used in the study of exponential functions and natural logarithms.
What is the relationship between Euler's number and the natural logarithm?
-The natural logarithm is the logarithm with Euler's number as its base. It is denoted as 'ln(x)' and is the inverse function of the exponential function with base 'e'. This relationship is fundamental in calculus and various mathematical applications.
How does the compound interest formula relate to Euler's number?
-The compound interest formula, which calculates the future value of an investment with compounding interest, can be used to derive Euler's number. By increasing the number of compounding periods and letting them approach infinity, the formula approaches the limit that defines Euler's number.
What is the significance of the number pi in mathematics?
-The number pi (π) is a mathematical constant that represents the ratio of a circle's circumference to its diameter. It is an irrational number and is fundamental in geometry, trigonometry, and various other areas of mathematics.
How does Euler's number compare to the number pi in terms of importance?
-Both Euler's number and pi are equally important in mathematics, each having unique applications. Pi is essential in geometry and trigonometry, while Euler's number is crucial in exponential growth, logarithms, and calculus.
What is the significance of the number e in the context of exponential growth?
-In the context of exponential growth, Euler's number e is the base of the exponential function that naturally arises when studying continuous growth processes. It represents the limit of compounding growth as the number of compounding periods approaches infinity.
What are some properties of the exponential function e^x?
-The exponential function e^x has several unique properties. Notably, its derivative at any point is equal to the function value at that point, and the area under the curve from negative infinity to any point x is equal to the function value at x. These properties make it a fundamental function in calculus.
What is Euler's formula, and why is it considered beautiful in mathematics?
-Euler's formula is e^(iπ) + 1 = 0. It is considered beautiful because it elegantly connects five fundamental mathematical constants: e, i (the imaginary unit), π, 1, and 0. This equation is a highlight of the deep interconnections in mathematics.
How does the concept of compounding interest lead to the discovery of Euler's number?
-By considering a 100% annual interest rate compounded increasingly frequently (e.g., daily, monthly, continuously), the formula for the future value of an investment approaches a limit as the compounding periods increase without bound. This limit is Euler's number, illustrating the natural emergence of 'e' from the process of exponential growth.
Outlines
📚 Introduction to Euler's Number e
The script introduces Euler's number e, a fundamental constant in mathematics, and its significance in the context of natural logarithms and exponential functions. It explains that e is an irrational number, much like pi, and is integral to various mathematical disciplines, including calculus. The video aims to explore the origin of e, emphasizing its natural emergence in exponential growth and decay processes, and its equivalence in status to pi, despite being introduced later in the mathematical curriculum.
🌱 The Natural Growth of Number e
This paragraph delves into the concept of exponential growth as the natural process from which the number e arises. It contrasts e with other special numbers like pi, which comes from geometry, and explains that e's significance is due to its prevalence in calculations involving exponential growth, such as compound interest. The script also begins to explore the compound interest formula as a means to understand the derivation of e, starting with an example of an annual 100% interest rate.
📈 The Compounding Effect on Euler's Number
The script continues to explain how the number e is derived from the compound interest formula by increasing the frequency of compounding. It illustrates the process by comparing the outcomes of compounding annually, semi-annually, monthly, and daily, showing that as the number of compounding periods increases, the growth factor approaches a limit. This limit is identified as Euler's number e, highlighting the relationship between frequent compounding and the emergence of e.
🔍 Approaching the Limit of Compounding
The discussion advances to the concept of continuous compounding, where the number of compounding periods becomes infinitesimally small, approaching a limit. The script demonstrates that as the compounding periods increase without bound, the growth factor converges to the number e. It provides numerical examples, showing how the growth factor approaches e as the compounding intervals become more frequent, eventually discussing the mathematical concept of a limit as the number of compounding periods approaches infinity.
🎯 The Definition and Properties of Euler's Number
The script defines Euler's number e as the limit of (1 + 1/n)^n as n approaches infinity, emphasizing its irrational nature with non-repeating, infinite decimals. It explains that e is a fundamental number in advanced mathematics, particularly in calculus, and is approached by increasing the frequency of compounding in the context of exponential growth. The importance of e is further underscored by its role in exponential functions and natural logarithms, which are central to calculus.
🌟 The Ubiquity and Importance of Euler's Number
This paragraph underscores the pervasiveness and importance of Euler's number e in advanced mathematical fields, suggesting that it appears even more frequently than pi in certain contexts. It outlines the properties of the exponential function with e as its base, highlighting its unique characteristic where the slope of the function at any point is equal to the function's value at that point. The script also touches on the significance of e in various mathematical equations and its foundational role in calculus.
🌀 Euler's Formula and the Beauty of Mathematics
The script concludes by introducing Euler's formula, which is often hailed as one of the most beautiful equations in mathematics due to its elegant integration of five fundamental mathematical constants: e, i, pi, 1, and 0. It explains that this formula encapsulates the harmony between these constants and provides a glimpse into the profound interconnectedness of mathematical concepts, leaving the audience with an appreciation for the elegance and depth of mathematical principles.
Mindmap
Keywords
💡Euler's number
💡Natural logarithm
💡Exponential growth
💡Compound interest
💡Irrational number
💡Exponential function
💡Limit
💡Natural exponential function
💡Derivative
💡Euler's formula
Highlights
Introduction to Euler's number e, a fundamental constant in mathematics.
Explanation of e as the base of the natural logarithm and its importance in exponential calculations.
Comparison of the significance of e with the mathematical constant pi.
Definition of e as an irrational number with a non-repeating, infinite decimal expansion.
Historical context of e, named after the mathematician Leonhard Euler.
The ubiquity of e in various disciplines of science, engineering, and advanced mathematics.
Discussion on the special exponential function e^x and its unique properties.
Introduction to the natural logarithm as the inverse function of the exponential function with base e.
The natural logarithm's notation Ln(X) and its distinction from other logarithms.
The natural occurrence of e in equations related to exponential growth, similar to pi in geometry.
Exploration of the derivation of e through the compound interest formula.
Demonstration of how increasing compounding frequency leads to values approaching e.
The concept of continuous compounding and its relationship to the limit definition of e.
Calculation of e using the limit of (1 + 1/n)^n as n approaches infinity.
The unique graphical properties of the exponential function e^x, where the slope equals the function's value.
Euler's formula, e^(iπ) + 1 = 0, showcasing the interrelation of fundamental mathematical constants.
The pervasiveness of e in advanced mathematical fields such as calculus and differential equations.
Transcripts
Browse More Related Video
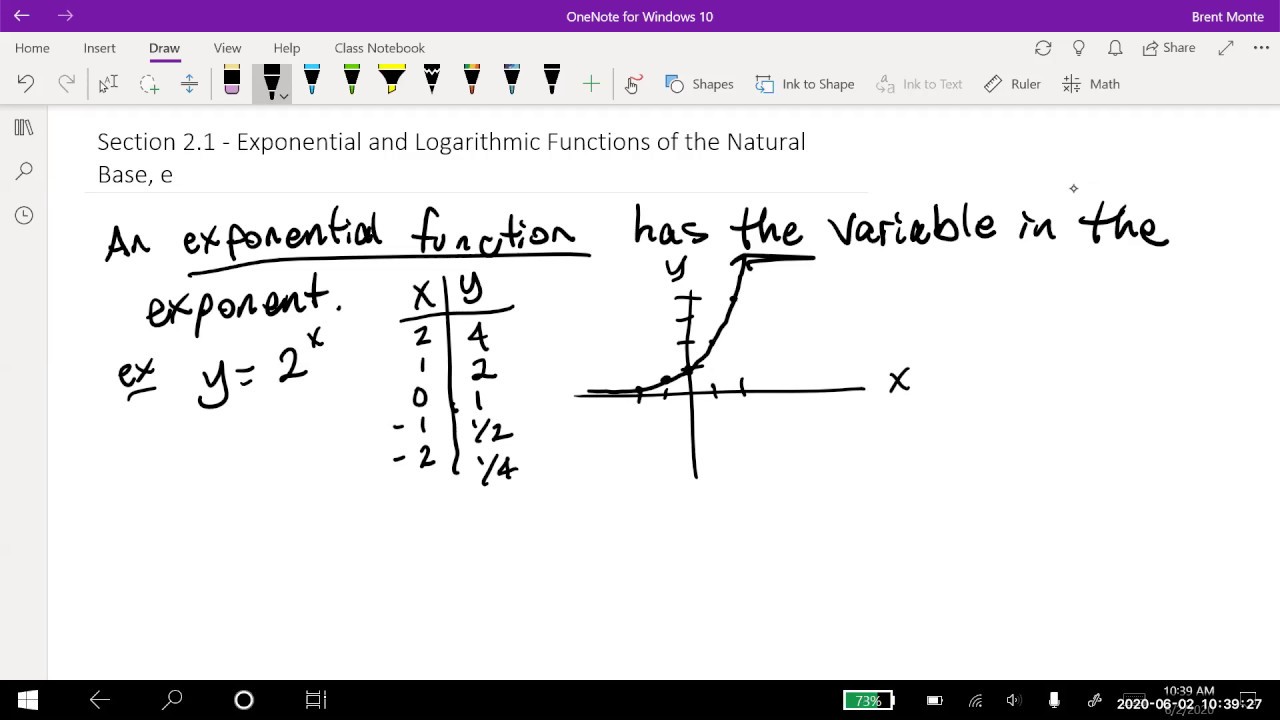
Math 11 - Section 2.1

Calculus 2 Lecture 6.3: Derivatives and Integrals of Exponential Functions

What is e and ln(x)? (Euler's Constant and The Natural Logarithm)

Euler's formula & Euler's identity | Series | AP Calculus BC | Khan Academy

Ch. 4.2 The Natural Exponential Function

Approximating functions with polynomials (part 3)
5.0 / 5 (0 votes)
Thanks for rating: