What is e and ln(x)? (Euler's Constant and The Natural Logarithm)

Mathacy
17 Jan 202112:01
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the significance of exponential functions in mathematics, highlighting their applications in modeling population growth, financial compound interest, and the discovery of Euler's constant (e). It explains how different interest rates over varying periods can be compared using exponential functions, ultimately leading to the concept of continuous compounding and its maximum value. The script also explores the differentiation of exponential functions, introducing the natural logarithm and its properties, and demonstrates how it can be used to solve integrals and understand phenomena like radioactive decay. The video aims to familiarize viewers with these fundamental mathematical concepts.

Takeaways
  • 📈 Exponential functions are crucial in mathematics for modeling various scenarios like population growth and financial compound interest.
  • 🏦 The concept of compound interest demonstrates the power of exponential growth, with more frequent interest compounding leading to higher returns.
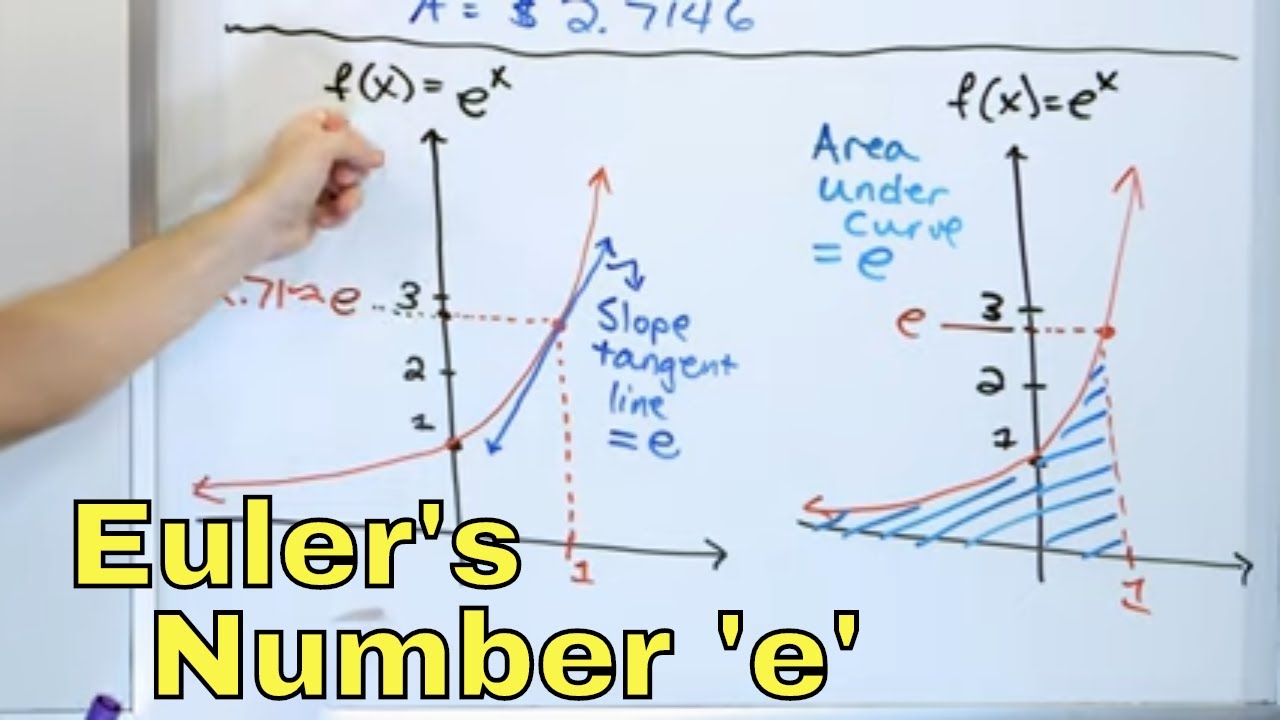
  • 🎯 The mathematical constant e (approximately 2.71828) is derived from the limit of (1 + 1/n)^n as n approaches infinity, representing the maximum growth rate.
  • 🔄 The number e is historically significant as it relates to the growth rate not just in mathematics but also in real-world applications like banking interest.
  • 📚 The process of differentiating exponential functions reveals that the derivative of a function like a^x is a constant multiple (k) of the function itself (a^x).
  • 🚀 The function e^x is unique in that its derivative is itself, making it one of the fastest-growing functions in mathematics, relevant to modeling rapid changes like infectious disease spread.
  • 📊 The natural logarithm (ln x) is the inverse function of e^x, and it has important properties that are useful in mathematics, such as the logarithm of a product being the sum of logarithms.
  • 🌿 The concept of natural logarithms is applied in real-world scenarios like calculating radioactive decay, where the substance's mass reduces to half its amount after a certain period.
  • 🌐 The video script emphasizes the importance of understanding exponential and logarithmic functions for anyone on a mathematical journey, as they are encountered frequently.
  • 📝 The video provides a comprehensive overview of exponential functions, their growth patterns, and their applications, as well as the natural logarithm and its relationship with e.
  • 🔗 The video encourages viewers to explore more about mathematics and provides resources for further learning, such as the website mathesy.com.
Q & A

  • What are exponential functions used for in mathematics?

    -Exponential functions are used to model various scenarios such as population growth, the spread of infectious diseases, and financial calculations like compound interest.

  • How does the concept of compound interest relate to exponential functions?

    -Compound interest demonstrates the power of exponential growth. The more frequently interest is compounded, the greater the final amount, illustrating the exponential nature of growth in financial contexts.

  • What is the significance of the number e in mathematics?

    -The number e, approximately equal to 2.71828, is known as Euler's constant and is the base of the natural logarithm. It is significant because it represents the maximum growth rate for compound interest as n approaches infinity.

  • How does the concept of limits relate to the number e?

    -The number e can be defined as the limit of (1 + 1/n)^n as n approaches infinity. This limit demonstrates the maximum value that can be achieved by the compound interest formula.

  • What is the derivative of an exponential function with base a?

    -The derivative of an exponential function y = a^x is a^x times a constant k, where k is a factor that depends on the base 'a'. For the base 'e', the constant k is 1, making the derivative equal to the original function, e^x.

  • What is the natural logarithm and how is it related to exponential functions?

    -The natural logarithm, denoted as ln(x) or log base e of x, is the inverse function of the exponential function e^x. It is used to solve for x in an exponential equation and has important properties in calculus and mathematics.

  • What is a key property of logarithms that relates to the derivative of the natural logarithm function?

    -A key property of logarithms is that the logarithm of a product is the sum of the logarithms. This property, combined with the inverse relationship between exponentials and logarithms, leads to the derivative of ln(x) being 1/x.

  • How does the natural logarithm help in solving integrals?

    -The natural logarithm allows us to evaluate integrals that would otherwise be difficult to solve, such as the integral of 1/x dx, which is equal to ln|x| + C, where C is the constant of integration.

  • What is the exponential decay model and how does it relate to the natural logarithm?

    -The exponential decay model, such as the half-life of a radioactive substance, can be represented as y = (1/2)^x or equivalently as y = e^(-0.693*x). It demonstrates the natural logarithm's role in modeling processes that decrease exponentially over time.

  • Why is it useful to express exponential functions in terms of e rather than another base?

    -Expressing exponential functions in terms of e is useful because the derivative of e^x is simply e^x itself, and the natural logarithm of e^x is x. This simplifies calculations and makes the mathematics of exponential growth and decay more manageable.

  • What advice is given for students learning about exponential and logarithmic functions?

    -Students are encouraged to become familiar with these functions and understand their properties and applications, as they are fundamental to many areas of mathematics and will be encountered frequently in their mathematical studies.

Outlines
00:00
📈 Exponential Functions and Compound Interest

This paragraph introduces exponential functions as crucial mathematical tools for modeling various scenarios, such as population growth and financial compound interest. It delves into the historical discovery of the constant 'e' in the context of compound interest, explaining how different interest rates and periods affect the growth of an investment. The concept of continuous compounding is explored, leading to the introduction of Euler's number (e), which is approximately 2.71828. The paragraph also discusses the mathematical properties of exponential functions, such as their derivatives, and how they relate to real-world phenomena like the spread of infectious diseases.

05:01
🧮 Derivatives of Exponential Functions and Natural Logarithms

The second paragraph focuses on the derivatives of exponential functions, illustrating how to calculate the derivative of functions like y = a^x and revealing a constant 'k' that appears in the derivative expressions. It introduces the concept of the natural exponential function y = e^x, whose derivative is the function itself, highlighting its rapid growth. The paragraph then transitions to the natural logarithm function, explaining its relationship with exponential functions and its graphical representation. It also covers the properties of logarithms, such as the logarithm of a product and the relationship between exponentials and logarithms, and concludes with the differentiation of natural logarithms, emphasizing their importance in mathematics.

10:03
🌟 Applications and Real-Life Examples of Exponential Functions

The final paragraph discusses the practical applications of exponential functions, including the calculation of radioactive decay and the concept of half-life. It explains how exponential decay models can be rewritten using natural logarithms and Euler's number, facilitating mathematical manipulation. The paragraph emphasizes the importance of understanding exponential and logarithmic functions for anyone on a mathematical journey. It concludes with a call to action for viewers to engage with the content, explore further, and support the educational resources provided.

Mindmap
Keywords
💡Exponential Functions
Exponential functions are mathematical functions that model growth or decay processes. In the video, they are used to model scenarios such as population growth and financial compound interest. The function's rate of growth increases as the value of the independent variable (often time) increases. An example from the script is the calculation of compound interest, where the amount of money doubles every year if the interest rate is 100%.
💡Compound Interest
Compound interest is the interest on a loan or deposit that is calculated based on both the initial principal and the accumulated interest from previous periods. It illustrates the power of exponential functions in finance, as the total amount grows at an increasing rate over time. The video explains how different compounding frequencies lead to different growth rates, with more frequent compounding leading to higher final amounts.
💡Euler's Number (e)
Euler's number, denoted by 'e', is a fundamental mathematical constant approximately equal to 2.71828. It is the base of the natural logarithm and is the limit of (1 + 1/n)^n as n approaches infinity. In the context of the video, 'e' is introduced as the maximum growth factor for compound interest, where the amount of money grows most when interest is compounded continuously.
💡Derivative
The derivative of a function is a measure of how the function changes as its input changes. It is a fundamental concept in calculus and is used to analyze the rate of change or slope of a function at any given point. In the video, the derivative is used to find the rate of change of exponential functions, such as 2^x, and natural logarithm functions, such as ln(x).
💡Natural Logarithm
The natural logarithm, denoted as ln(x), is the logarithm to the base 'e'. It is the inverse function of the exponential function with base 'e', meaning that e^(ln(x)) equals x. Natural logarithms are used in various mathematical and real-world applications, including solving exponential equations and calculating growth rates.
💡Interest Rates
Interest rates are the percentage at which interest is paid by borrowers to lenders. They are crucial in finance for calculating the cost of borrowing and the return on investments. In the video, different interest rates are compared to demonstrate how they affect the growth of an investment over time.
💡Infinite Limit
The concept of an infinite limit refers to the value that a function or sequence approaches as the input tends towards infinity or some other specified value. In the video, the limit is used to define Euler's number 'e' and to find the maximum growth rate of compound interest.
💡Chain Rule
The chain rule is a fundamental principle in calculus used to find the derivative of a composite function. It states that the derivative of a function composed of two or more functions is the derivative of the outer function times the derivative of the inner function. In the video, the chain rule is implied when discussing the derivative of exponential functions.
💡Radioactive Decay
Radioactive decay is a natural process in which an unstable atomic nucleus loses energy by emitting radiation. In the video, it is used as an example of an exponential decay process, where the quantity of a radioactive substance decreases exponentially over time.
💡Harmonic Series
The harmonic series is the sum of the reciprocals of the natural numbers, often denoted as 1 + 1/2 + 1/3 + ... In the video, it is mentioned as an example of a series that diverges to infinity, contrasting with the finite value of the integral of 1/x, which is shown to be equal to ln(x).
💡Inverse Functions
Inverse functions are functions that 'undo' the operation of another function. If one function takes an input and produces an output, its inverse function takes that output and returns the original input. In the video, the concept is used to describe the relationship between exponential and logarithmic functions, which are inverses of each other.
Highlights

Exponential functions are crucial in mathematics for modeling various scenarios such as population growth and financial interest.

The number e, or the natural logarithm base, was historically discovered in the context of calculating compound interest.

Compound interest demonstrates the power of exponential growth, where more frequent interest compounding leads to higher returns.

The mathematical limit as n approaches infinity of (1 + 1/n)^n results in the irrational number e, approximately equal to 2.71828.

Exponential functions can be differentiated to reveal important constants such as k2, which is approximately 0.6931.

The function y = e^x is unique in that its derivative is itself, making it one of the fastest-growing functions in mathematics.

Natural logarithms are the inverse functions of exponentials and have properties that make them extremely useful in mathematics.

The natural logarithm function ln(x) has a derivative of 1/x, which has significant implications for integration and series convergence.

The relationship between exponentials and logarithms allows for the transformation of expressions like a^x into e^(ln(a)x), simplifying many mathematical processes.

Radioactive decay can be modeled using exponential functions, demonstrating the practical applications of these mathematical concepts.

The harmonic series, which sums 1/n for all natural numbers n, diverges to infinity due to the logarithmic nature of its terms.

Exponential functions are written as e^(kx) to leverage the properties of e and the natural logarithm, simplifying derivatives and integrals.

Understanding exponential and logarithmic functions is essential for a comprehensive mathematical education and their applications are widespread.

The video provides a comprehensive exploration of exponential functions, their properties, and applications in various mathematical contexts.

Transcripts

Browse More Related Video

Business Calculus - Math 1329 - Section 4.1 - Exponential Functions and Continuous Compounding

14 - What is Euler's Number 'e', Ln(x) - Natural Log & e^x Functions?

Math 11 - Section 2.1

2.2 - Derivatives of Exponential Functions

Ch. 4.2 The Natural Exponential Function

What's so special about Euler's number e? | Chapter 5, Essence of calculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Exponential FunctionsCompound InterestEuler's NumberNatural LogarithmCalculusFinancial ModelingPopulation GrowthRadioactive DecayDifferential CalculusMathematical Concepts