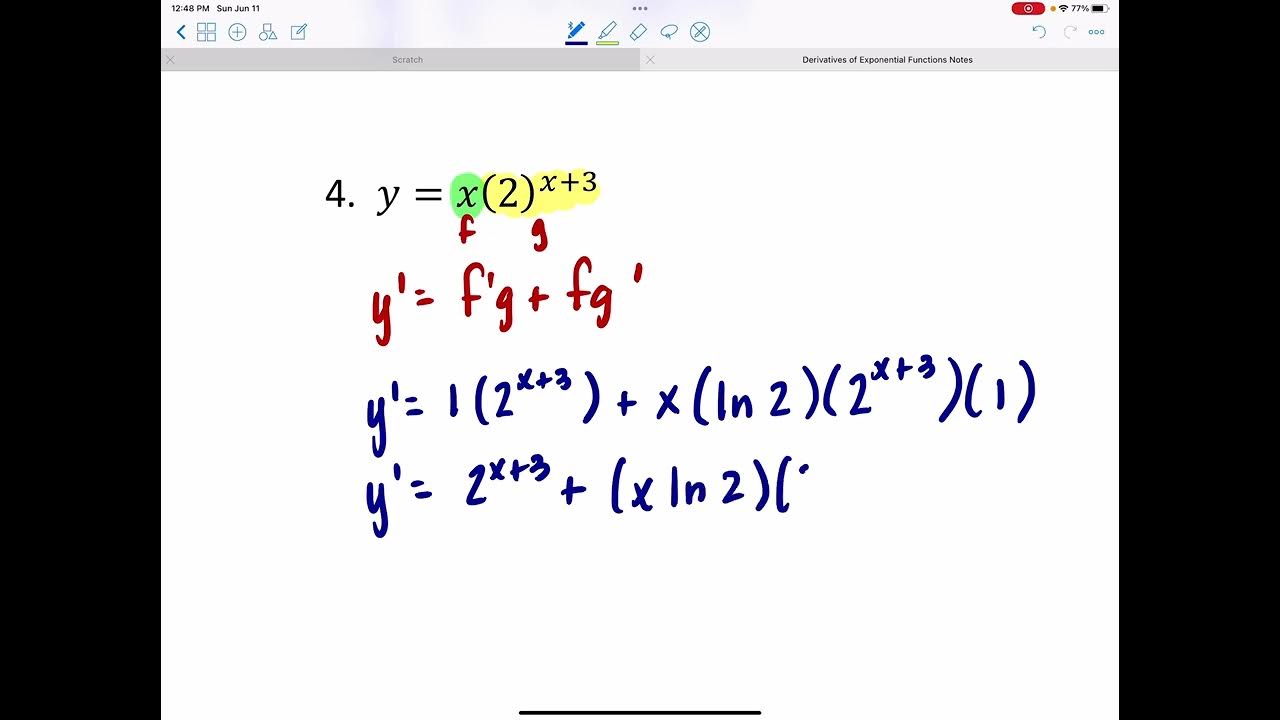
Ch. 4.2 The Natural Exponential Function

Prof. Williams
27 Feb 202214:57
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video delves into Chapter 4.2 on the natural exponential function, drawing parallels with the exponential function from the previous chapter. It explores the concept of compound interest, demonstrating how the frequency of compounding affects the growth of investment. The video introduces the value of 'e', the base of natural logarithms, as the limit of (1 + 1/n)^n as n approaches infinity. It also discusses the natural exponential function, e^x, and its application in continuously compounded interest. Additionally, the script touches on hyperbolic functions, specifically sinh and cosh, which are defined using the exponential base 'e' and graphed, showing their relationship to exponential growth.

Takeaways
  • 📈 The natural exponential function, discussed in chapter 4.2, is closely related to the exponential function from chapter 4.1.
  • 💰 As the frequency of compounding an investment increases, the amount received in interest also increases but stabilizes at a certain value.
  • 🔢 The formula used to observe the behavior of compounding is 1 + 1/n to the n, where n is the number of compounding periods.
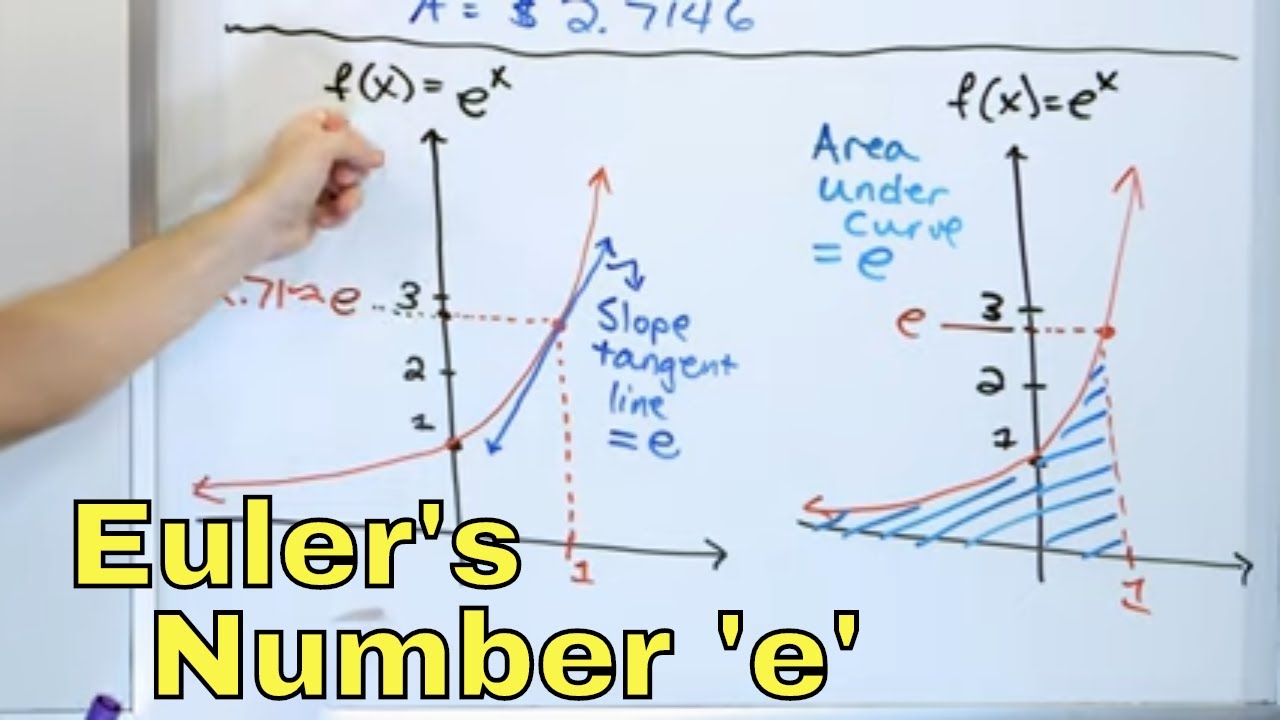
  • 📊 When compounding continuously, the value approaches the mathematical constant e, approximately 2.718281.
  • 🔄 e is an irrational number, similar to π, and it is used as the base for natural exponential functions.
  • 🧮 The natural exponential function is defined as f(x) = e^x, where e is a constant and not a variable.
  • ⏳ Continuous compounding is used in situations where the compounding is happening all the time without any discrete intervals.
  • 💸 For example, continuously compounding an initial investment of $2500 at 0.5% for 5 years results in approximately $2563.29.
  • 🌀 Hyperbolic functions, similar to trigonometric functions but related to hyperbolas, include hyperbolic sine (sinh) and hyperbolic cosine (cosh).
  • 📉 Hyperbolic sine (sinh) and hyperbolic cosine (cosh) are defined using the exponential base e, with sinh(x) = (e^x - e^-x) / 2 and cosh(x) = (e^x + e^-x) / 2.
Q & A

  • What is the main topic of Chapter 4.2?

    -The main topic of Chapter 4.2 is the natural exponential function.

  • How does the natural exponential function relate to the previous section, Chapter 4.1?

    -Chapter 4.2 is very similar to Chapter 4.1, which discussed the exponential function. Both chapters explore the concept of exponential growth, but Chapter 4.2 focuses specifically on the natural exponential function.

  • What happens to the amount of interest received when the number of times we compound an investment increases?

    -As the number of times we compound an investment increases, the amount of interest received also increases. However, this increase approaches a certain value and does not go to infinity.

  • What is the significance of the formula \(1 + \frac{1}{n}\) raised to the power of \(n\)?

    -The formula \(1 + \frac{1}{n}\) raised to the power of \(n\) is used to explore the behavior of compound interest as the number of compounding periods increases. It demonstrates that as \(n\) increases, the value of this expression approaches the number \(e\).

  • What value does the expression \(1 + \frac{1}{n}\) raised to the power of \(n\) approach as \(n\) becomes very large?

    -As \(n\) becomes very large, the expression \(1 + \frac{1}{n}\) raised to the power of \(n\) approaches the value \(e\), which is approximately 2.718281.

  • Why is \(e\) considered an important number in mathematics?

    -The number \(e\) is important because it is the base of the natural exponential function. It appears in many areas of mathematics, particularly in calculus, and is used to model continuous growth processes.

  • How is the natural exponential function defined?

    -The natural exponential function is defined as \(f(x) = e^x\), where \(e\) is the base of the natural exponential function.

  • What is the formula for continuously compounded interest?

    -The formula for continuously compounded interest is \(P e^{rt}\), where \(P\) is the principal amount, \(r\) is the interest rate, and \(t\) is the time.

  • What are hyperbolic functions and how do they relate to exponential functions?

    -Hyperbolic functions are functions defined using the exponential base \(e\). They are analogous to trigonometric functions but are related to hyperbolas instead of circles. The basic hyperbolic functions are the hyperbolic sine (sinh) and hyperbolic cosine (cosh).

  • How are the hyperbolic sine and cosine functions defined?

    -The hyperbolic sine (sinh) function is defined as \(sinh(x) = \frac{e^x - e^{-x}}{2}\), and the hyperbolic cosine (cosh) function is defined as \(cosh(x) = \frac{e^x + e^{-x}}{2}\).

Outlines
00:00
📈 Exploring the Natural Exponential Function

In this section, we delve into Chapter 4.2, focusing on the natural exponential function, which closely relates to the exponential function discussed in Chapter 4.1. The discussion begins with compound interest, observing how increased compounding frequencies boost interest returns. The function 1 + (1/n)^n is examined as n approaches infinity, revealing that the investment growth stabilizes at a specific value rather than growing infinitely. By setting variables P, R, and T to one, the analysis simplifies to observing 1 + (1/n)^n for various n values, showing it approaches the value of 'e' (approximately 2.718281) as n increases.

05:00
📊 Stabilizing Towards the Value of 'e'

Continuing from the previous analysis, as n increases to very large values (like 1 million or 10 million), the value of 1 + (1/n)^n stabilizes closely around 2.718281, denoted as 'e'. This number is an irrational constant, much like π, and it plays a crucial role in exponential functions. The script highlights that the function 1 + (1/n)^n approaches 'e' as n becomes exceedingly large, illustrating this with increasingly accurate values and reinforcing the importance of 'e' in continuous compounding and exponential growth scenarios.

10:02
🔢 Continuous Compounding and the Natural Exponential Function

The concept of continuous compounding is introduced, where interest is compounded constantly rather than periodically. The function P * e^(RT) is used to calculate the future value of an investment under continuous compounding. Using a previous example of investing $2500 at an interest rate of 0.5% for five years, the future value is calculated to be $2563.29, slightly higher than daily compounding. This section also introduces hyperbolic functions, which, unlike trigonometric functions, relate to hyperbolas rather than circles. The basic hyperbolic functions, sinh (cinch) and cosh (cosh), are defined using the exponential base 'e'.

Mindmap
Keywords
💡Natural Exponential Function
The natural exponential function is a mathematical function of the form e^x, where e is Euler's number, approximately 2.71828. It is central to the video's theme as it explores the properties and applications of exponential growth, particularly in continuously compounded interest. The script discusses how this function stabilizes towards the value of e as the number of compounding periods increases.
💡Compound Interest
Compound interest refers to the interest calculated on the initial principal, which also includes all accumulated interest from previous periods. The video uses this concept to illustrate how increasing the frequency of compounding results in a higher amount of interest accrued, demonstrating the behavior of the exponential function.
💡Euler's Number (e)
Euler's number, denoted as e, is an irrational number approximately equal to 2.71828. It is the base of the natural logarithm and a fundamental constant in mathematics. In the video, e emerges as the limit of (1 + 1/n)^n as n approaches infinity, showing its importance in continuous growth models and natural exponential functions.
💡Continuously Compounded Interest
Continuously compounded interest is a scenario where interest is calculated and added to the principal at every possible instant. The formula for this type of interest is A = Pe^rt. The video contrasts this with regular compounding, illustrating how continuous compounding slightly increases the final amount over discrete compounding periods.
💡Hyperbolic Functions
Hyperbolic functions, such as sinh (hyperbolic sine) and cosh (hyperbolic cosine), are analogs of trigonometric functions but for a hyperbola instead of a circle. The video introduces these functions, showing their definitions in terms of e^x and their relevance to the natural exponential function. They demonstrate the diverse applications of e beyond simple exponential growth.
💡Exponential Growth
Exponential growth refers to the increase of a quantity at a consistent relative growth rate, leading to a rapid rise over time. The video explains this concept through continuously compounded interest, where the value of an investment grows exponentially over time, emphasizing the role of e in modeling such phenomena.
💡Irrational Number
An irrational number is a number that cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion. Euler's number e is an example, as highlighted in the video. The script discusses how e does not repeat and continues indefinitely, similar to the properties of π.
💡Natural Base
The natural base, denoted by e, is the foundation of natural exponential functions. It arises naturally in various mathematical contexts, particularly in continuous growth models. The video explains its derivation and importance in defining functions like f(x) = e^x and in calculating continuously compounded interest.
💡Initial Value (P)
The initial value, often represented as P, is the starting amount before any growth or interest accumulation. In the context of the video, it refers to the principal amount invested in a compound interest scenario. Understanding this concept is crucial for applying formulas like A = Pe^rt to determine future values of investments.
💡Exponential Function
An exponential function is a mathematical function in which an independent variable appears in the exponent. In the video, the function f(x) = e^x is a key focus, illustrating how exponential growth works and how the function behaves as its variable increases. This function is pivotal in modeling continuous growth and decay processes.
Highlights

Introduction to chapter 4.2: the natural exponential function.

Comparison of the natural exponential function with the previous section on the exponential function.

Discussion on compound interest and how increasing the frequency of compounding increases the amount of interest received.

Explanation of the function 1 + 1/n to the power of n, and how it stabilizes as n approaches infinity.

Demonstration of the function with different values of n, showing the approach to the value e.

Clarification that the value e is approximately 2.71828 and is an irrational number like pi.

Introduction to the concept of continuously compounding interest using the formula P * e^(rt).

Example of calculating continuously compounded interest for an investment.

Introduction to hyperbolic functions: hyperbolic sine (sinh) and hyperbolic cosine (cosh).

Explanation of the formulas for sinh and cosh and their similarity to exponential functions.

Graphical representation of sinh and cosh functions.

Discussion on the relationship between hyperbolic functions and exponential growth.

Comparison of hyperbolic functions to trigonometric functions.

Explanation of the transformations involved in the graphs of sinh and cosh.

Summary of the significance of the natural exponential function and its applications in various continuous growth scenarios.

Transcripts

Browse More Related Video

Derivatives of Exponential Functions

Math1325 Lecture 11 2 - Derivatives of Exponential

Ch. 4.1 Exponential Functions

Lec 6 | MIT 18.01 Single Variable Calculus, Fall 2007

14 - What is Euler's Number 'e', Ln(x) - Natural Log & e^x Functions?

2.2 - Derivatives of Exponential Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Exponential FunctionContinuous CompoundingHyperbolic FunctionsMathematics EducationInvestment GrowthTrigonometric AnaloguesNatural BaseEuler's NumberFinancial MathEducational ContentMath Concepts