Ch. 10.2 Systems of Linear Equations in Several Variables
TLDRThis educational video script introduces the concept of solving systems of linear equations with multiple variables using the elimination method, also known as Gaussian elimination. The instructor explains the process of systematically eliminating variables to simplify the system into a triangular form, making it easier to solve through back substitution. The script also discusses the three elementary operations allowed in this process: swapping equations, multiplying an entire equation by a non-zero scalar, and adding or subtracting equations to eliminate variables. The goal is to find the number of solutions, which can be one, none, or infinite, depending on the intersection of the represented planes in three-dimensional space.
Takeaways
- 📚 The class is focusing on Chapter 10.2, which discusses systems of linear equations with multiple variables, specifically starting with three equations in three variables.
- 🔍 The elimination method is introduced as the primary technique for solving larger systems of equations, as it is more practical than graphing or substitution for systems with many variables.
- 📉 The graphing method is deemed impractical for equations with more than three variables due to the inability to visualize higher-dimensional spaces.
- 🔄 The elimination method involves repeatedly adding or subtracting equations to eliminate one variable at a time, aiming to simplify the system into a triangular form.
- 🔢 The process aims to isolate the first variable in the first equation, the second variable in the second equation, and so on, creating a system that resembles a ladder for easy back substitution.
- 🔄 The term 'triangular system' is used because the simplified system resembles a triangle, with each variable isolated in descending order.
- 🔑 Back substitution is the final step in solving the system, where known values are substituted back into previous equations to find the remaining variables.
- 🚫 Only three elementary operations are allowed during the elimination process: swapping equations, multiplying an entire equation by a non-zero scalar, and adding/subtracting equations or multiples of equations.
- 📝 The process of using these operations to transform a system into a triangular form is known as Gaussian elimination, named after the mathematician Carl Friedrich Gauss.
- 🤔 The number of solutions to a system of linear equations is consistent, being either one solution, no solutions, or infinite solutions, depending on the intersection of the represented planes in space.
- 📈 An example is provided to illustrate the process of Gaussian elimination, demonstrating how to transform a system of equations into triangular form and solve for the variables step by step.
Q & A
What is the main topic of this lecture?
-The main topic of this lecture is solving systems of linear equations, specifically focusing on methods for handling systems with three equations and three variables, extending the discussion to systems with more equations and variables.
Why is the elimination method preferred over graphing and substitution for systems with many variables?
-The elimination method is preferred because graphing is impossible for equations with more than three variables, and substitution becomes impractical with a large number of variables due to the extensive work required to substitute variables multiple times.
What is the general principle behind the elimination method discussed in the lecture?
-The general principle behind the elimination method is to systematically eliminate one variable at a time by adding or subtracting equations from each other until a triangular system is formed, which simplifies the process of solving the system.
What is a triangular system in the context of solving equations?
-A triangular system refers to a set of equations that have been arranged in such a way that each equation has one more variable than the one below it, forming a 'triangle' shape. This makes it easier to solve for the variables by back substitution.
What is back substitution and why is it used after forming a triangular system?
-Back substitution is the process of solving for the variables in reverse order, starting from the last equation, after a system of equations has been transformed into a triangular form. It is used because it simplifies the solving process by allowing you to find the value of one variable at a time and then substitute it back into the previous equations.
What are the three elementary operations allowed during the process of Gaussian elimination?
-The three elementary operations allowed during Gaussian elimination are: 1) Swapping two equations, 2) Multiplying an entire equation by a non-zero scalar, and 3) Adding or subtracting one equation to or from another equation or a multiple of another equation.
Who is the famous mathematician mentioned in the script, known for the method of solving systems of equations?
-The famous mathematician mentioned in the script is Carl Friedrich Gauss, who is known for developing the method of Gaussian elimination for solving systems of equations.
What are the possible number of solutions for a system of linear equations?
-For a system of linear equations, there can be either one solution, no solutions, or infinite solutions. This is true regardless of the number of dimensions of the system.
How can you determine if a system of equations has no solution or infinite solutions?
-A system of equations has no solution if the planes (in the case of three dimensions) do not intersect at any common point. It has infinite solutions if all the planes intersect along a line, indicating that there are infinitely many points of intersection.
Can you provide an example of the process of Gaussian elimination as demonstrated in the lecture?
-Yes, the lecture provides an example where the system of equations is manipulated through elementary operations to form a triangular system. The equations are then solved using back substitution, starting with the last equation and moving upwards, solving for each variable in turn.
What is the significance of the term 'Gaussian elimination' in the context of this lecture?
-The term 'Gaussian elimination' refers to the specific method of solving systems of equations by using elementary operations to eliminate variables and form a triangular system. The name comes from the mathematician Carl Friedrich Gauss, who developed this method.
Outlines
📚 Introduction to Solving Systems of Linear Equations
The instructor begins by introducing the topic of solving systems of linear equations with multiple variables, focusing on three equations and three variables as a starting point. The discussion extends to the concept of n equations with n variables. The preferred method for solving larger systems is the elimination method, which involves adding or subtracting equations to eliminate variables step by step. The instructor emphasizes that while the graphing method is not feasible for systems with more than three variables, the substitution method is still applicable but can be laborious. The goal of the elimination method is to systematically reduce the system to a triangular form, which simplifies the process of back substitution to find the values of the variables.
🔍 Understanding the Elimination Method and Gaussian Elimination
The instructor explains the elimination method in more detail, describing it as a process to systematically eliminate variables from the system of equations. The method involves elementary operations such as swapping equations, multiplying an entire equation by a non-zero scalar, and adding or subtracting equations to eliminate variables. These operations are fundamental to the Gaussian elimination process, named after the mathematician Carl Gauss. The instructor stresses the importance of using these operations correctly to maintain the integrity of the system's solutions. The concept of solutions to a system of equations is also discussed, noting that there are always either one solution, no solutions, or infinite solutions, depending on the intersection of the represented planes or lines.
📐 Demonstrating Gaussian Elimination with an Example
The instructor provides a practical example to illustrate the Gaussian elimination process. The example involves a system of three equations representing planes in three-dimensional space. The goal is to manipulate the system into a triangular form where each variable is isolated in its respective equation. The instructor demonstrates how to use elementary operations to eliminate variables step by step, transforming the system until it reaches a form where back substitution can be applied. The process involves careful manipulation of the equations to ensure that each variable is eliminated below its leading position in the system.
🧩 Completing the Solution with Back Substitution
Having transformed the system into triangular form, the instructor proceeds to solve for the variables using back substitution. The process involves solving the last equation for the last variable, then substituting this value into the second-to-last equation to solve for the next variable, and so on, moving backwards through the system. The example concludes with finding the values of x, y, and z, demonstrating that the system has a single solution. The instructor emphasizes the methodical nature of Gaussian elimination and back substitution as a reliable approach to solving systems of linear equations.
Mindmap
Keywords
💡Systems of Linear Equations
💡Elimination Method
💡Variables
💡Gaussian Elimination
💡Triangular System
💡Back Substitution
💡Elementary Operations
💡Coefficients
💡Planes
💡Solutions
💡Graphing Method
Highlights
Introduction to solving systems of linear equations with multiple variables using the elimination method.
Explanation of extending the discussion to systems with up to 20 equations and variables.
The graphing method is no longer viable for systems with more than three variables.
The substitution method remains applicable but is labor-intensive for systems with many variables.
Emphasis on the elimination method as the primary technique for solving large systems of equations.
The goal of the elimination method is to systematically eliminate one variable at a time.
Description of the triangular system formation for ease of solving through back substitution.
The process of back substitution explained for solving the system once in triangular form.
Introduction of elementary operations allowed in the elimination process: swapping equations, multiplying by a non-zero scalar, and adding/subtracting equations.
The concept of Gaussian elimination as a systematic approach to variable elimination.
Gauss, the mathematician, credited with the development of Gaussian elimination.
The three possible outcomes for a system of equations: one solution, no solutions, or infinite solutions.
Visual representation of solutions in three-dimensional space with planes.
Demonstration of solving a system of three equations representing planes in three dimensions.
Step-by-step walkthrough of Gaussian elimination applied to an example system of equations.
Technique of swapping equations to facilitate easier elimination of variables.
Final solution of the example system using back substitution after achieving triangular form.
Summary of the Gaussian elimination process and its application to systems of linear equations.
Transcripts
Browse More Related Video

PreCalculus - Matrices & Matrix Applications (9 of 33) Gaussian Elimination: 3x3, Infinite Solutions

Ch. 10.1 Systems of Linear Equations in Two Variables

Ch. 10.3 Matrices and Systems of Linear Equations

Gaussian Elimination & Row Echelon Form

A Guide to Gaussian Elimination Method (and Solving Systems of Equations) | Linear Algebra
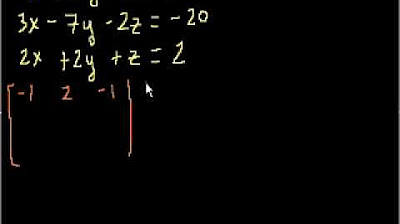
Solving 3 Equations with 3 Unknowns
5.0 / 5 (0 votes)
Thanks for rating: