Solving 3 Equations with 3 Unknowns

Khan Academy
11 Apr 200915:26
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explains the process of solving a system of linear equations with two and three unknowns. It begins with the visual concept of lines intersecting to find a solution and progresses to the more complex three-dimensional analogy of planes intersecting. The method of Gaussian elimination is introduced as a systematic way to solve such systems, with an example provided for three equations in three variables. The script concludes with the solution x=1, y=3, z=-2, demonstrating how to find the unique point of intersection.

Takeaways
  • 📚 The script explains the process of solving a system of linear equations with two and three unknowns.
  • 🤔 It introduces the concept of visual representation, where lines (for two unknowns) or planes (for three unknowns) intersect at a unique point representing the solution.
  • 🔢 The method of solving two equations with two unknowns involves manipulating the equations to eliminate one variable and find the solution at the intersection.
  • 📈 For three equations with three unknowns, the script introduces the concept of an augmented matrix to simplify the process.
  • 🌟 Gaussian elimination is mentioned as a systematic approach to solving such systems, which involves eliminating variables in a structured way.
  • 🔄 The script demonstrates the steps of Gaussian elimination with an example of a 3x3 system of equations, showing how to manipulate the augmented matrix to find the solution.
  • 👉 The process of back-substitution is highlighted as a way to find the remaining variables once one variable has been solved for.
  • 🎯 The importance of being systematic and methodical when solving complex systems of equations is emphasized to avoid confusion.
  • 📊 The script also touches on Gauss-Jordan elimination as a further step to refine the solution process, though it is not detailed in the example.
  • 😅 The speaker humorously mentions a personal anecdote about receiving phone calls, adding a relatable touch to the explanation.
  • 🍽️ The script concludes with a final solution to the provided 3x3 system of equations, where x = 1, y = 3, and z = -2.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is solving systems of linear equations with two and three unknowns using methods like scalar multiplication, elimination, and Gaussian elimination.

  • How are the equations visually represented in the context of the video?

    -The equations are visually represented as lines or planes in a coordinate system. Two equations with two unknowns represent lines in a two-dimensional space, while three equations with three unknowns represent planes in a three-dimensional space.

  • What is the significance of the intersection point of the lines or planes in the coordinate system?

    -The intersection point of the lines or planes is the solution to the system of equations. It represents the unique values of the unknowns that satisfy all the equations simultaneously.

  • How does the process of elimination work in solving systems of equations?

    -The process of elimination involves manipulating the equations by adding, subtracting, or multiplying to eliminate one or more variables. This simplifies the system and makes it easier to find the solution.

  • What is an augmented matrix and how is it used in solving systems of equations?

    -An augmented matrix is a matrix that contains the coefficients of the variables and the constants from the system of equations. It is used in Gaussian elimination to simplify the process of solving the system by focusing on the numerical values rather than the variables.

  • What is Gaussian elimination and how does it help in solving systems of equations?

    -Gaussian elimination is a method for solving systems of linear equations by transforming the augmented matrix into an upper triangular form through a series of row operations. This makes it easier to back-substitute values and find the solution to the system.

  • What is the solution to the example 3x3 system of equations provided in the video?

    -The solution to the example 3x3 system of equations is x = 1, y = 3, and z = -2. These values satisfy all three equations simultaneously.

  • How does the process of substitution work in solving systems of equations?

    -The process of substitution involves solving for one variable in one of the equations and then substituting that value into the other equations to solve for the remaining variables. This method is particularly useful when one equation is significantly simpler to solve for one variable.

  • What is the significance of the video's mention of the teacher's potential reaction to the use of augmented matrices?

    -The mention of the teacher's potential reaction highlights that while augmented matrices and Gaussian elimination can be more efficient and less prone to error, they may not always be the preferred method by all educators due to differences in teaching approaches or the complexity of the method.

  • What is the video speaker's attitude towards the computational process of solving the system of equations?

    -The video speaker finds the computational process intensive and not their preferred method, especially for a weekend task, but acknowledges its effectiveness in solving the system of equations.

  • What is the final step in solving the 3x3 system of equations in the video?

    -The final step in solving the 3x3 system of equations is to back-substitute the found values of z and y into the first equation to solve for x, thus finding the complete solution (x = 1, y = 3, z = -2).

Outlines
00:00
📚 Introduction to Solving Systems of Equations

This paragraph introduces the concept of solving systems of equations with two and three unknowns. It begins with a review of solving two-variable equations using linear representations as intersecting lines, and then transitions into a discussion on solving three-variable systems. The visual representation of three equations as intersecting planes in a three-dimensional space is mentioned, highlighting the complexity of finding the point where all three planes intersect.

05:04
🔢 Augmented Matrix and Gaussian Elimination

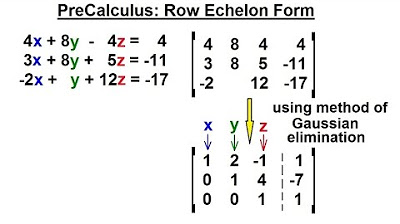
The paragraph delves into the method of using an augmented matrix to simplify the process of solving systems of equations. It explains the concept of Gaussian elimination, a systematic approach to solving three-variable equations. The process of eliminating variables is detailed, with a focus on the steps taken to reduce the system to a more manageable form. The paragraph also touches on the potential for computational intensity and the importance of a methodical approach.

10:06
📈 Solving the System: Elimination and Back Substitution

This section walks through the actual process of solving the given system of equations using the augmented matrix. It explains the steps of eliminating x and y terms to solve for z first, and then using back substitution to find the values of y and x. The paragraph provides a clear, step-by-step explanation of the calculations involved, leading to the solution of the system.

15:06
🎉 Conclusion and the Solution

The final paragraph wraps up the solution process by summarizing the solution found for the system of equations. It confirms the unique point in three-dimensional space where all three planes intersect, providing the values of x, y, and z. The speaker also shares a personal anecdote about needing to end the explanation to attend to other commitments, adding a touch of humor to the conclusion.

Mindmap
Keywords
💡Equations
Equations are mathematical statements that assert the equality of two expressions. In the context of the video, equations are used to represent relationships between variables (x, y, z) that are unknowns we are trying to solve for. The video discusses solving systems of equations with two and three unknowns, illustrating the process of finding the values of these variables that satisfy all equations simultaneously.
💡Lines
In the video, lines refer to the graphical representation of two-variable equations in a two-dimensional coordinate system. Each equation corresponds to a straight line, and the solution to a system of two equations is the point where these lines intersect. The concept extends to three dimensions for three-variable equations, where the intersections represent points in space.
💡Variables
Variables are symbols, often letters, that represent unknown quantities in equations. In the video, x, y, and z are variables that the presenter is trying to solve for within a system of equations. The process of finding their values is central to the content of the video.
💡Gaussian Elimination
Gaussian elimination is a systematic method for solving systems of linear equations by transforming the augmented matrix associated with the system into an upper triangular form through a series of row operations. The video uses this method to solve a system of three equations with three unknowns, emphasizing its importance for dealing with more complex systems.
💡Augmented Matrix
An augmented matrix is a matrix that combines the coefficients of a system of linear equations with the constants from the right-hand side of the equations. It is used as a visual tool to assist in the process of Gaussian elimination or other methods for solving systems of equations. The video introduces this concept as a more efficient way to manipulate and solve the system without repeatedly rewriting the equations.
💡Intersection
In the context of the video, intersection refers to the point or points where the graphical representations of equations (lines or planes) meet. For two-variable equations, the intersection is the solution to the system. For three-variable equations, the intersection represents the solution in three-dimensional space where all three planes meet.
💡Scalar
A scalar is a number that can be multiplied by a vector or used to scale (enlarge or reduce) the magnitude of a vector without changing its direction. In the context of the video, scalars are used to multiply equations in order to eliminate variables when solving systems of linear equations.
💡Substitution
Substitution is a mathematical method used to solve for an unknown by replacing it with an expression derived from another equation in the system. In the video, once one variable is solved for, its value is substituted back into other equations to solve for the remaining variables.
💡Three-Dimensional Space
Three-dimensional space is a geometric setting where every point can be determined by three coordinates, typically denoted x, y, and z. In the video, the presenter discusses the concept of three-variable equations representing planes in three-dimensional space, and the solution as the point where all three planes intersect.
💡Linear Equations
Linear equations are mathematical equations in which the highest power of the variables is one. They represent straight lines or planes in geometric terms and are the focus of the video, which explains how to solve systems of linear equations with two and three variables.
💡Row Operations
Row operations are a set of allowed transformations that can be performed on rows of a matrix or a system of linear equations. These operations include swapping rows, multiplying a row by a non-zero scalar, and adding or subtracting one row from another. In the video, row operations are used to manipulate the augmented matrix during Gaussian elimination.
Highlights

The introduction of solving a system of two equations with two unknowns using the concept of intersecting lines representing the solution.

The visual representation of equations as lines and the concept of non-parallel lines intersecting at a unique point.

The method of multiplying equations by scalars to eliminate variables and find the solution.

The transition from two-variable systems to three-variable systems and the analogy of planes intersecting in 3D space.

The introduction of Gaussian elimination as a systematic approach to solving systems of equations.

The explanation of augmented matrices as a time-saving tool for solving systems of equations.

The step-by-step process of eliminating variables using the augmented matrix method.

The computational process of transforming the system into upper row echelon form.

The solution of the three-variable system using the method of substitution after solving for one variable.

The final solution of the example 3x3 system (x=1, y=3, z=-2) and its significance as the unique point of intersection.

The mention of Gauss-Jordan elimination as a further step beyond Gaussian elimination for complete reduction of the matrix.

The practical application of the concepts discussed in the video for solving real-world problems.

The humorous anecdote about the speaker's phone ringing, possibly his wife calling, adding a touch of relatability and human connection.

The emphasis on the importance of being systematic when solving complex systems of equations.

The clear and detailed explanation of each step in the process, making the complex topic more accessible.

Transcripts

Browse More Related Video

Ch. 10.1 Systems of Linear Equations in Two Variables

Solving 3 Equations for 3 Unknowns Using a Matrix in Row Echelon Form

PreCalculus - Matrices & Matrix Applications (3 of 33) Row Echelon Form

PreCalculus - Matrices & Matrix Applications (7 of 33) Method of Gaussian Elimination: 3x3 Matrix*

Ch. 10.2 Systems of Linear Equations in Several Variables

SOLVING SYSYEM OF NONLINEAR EQUATIONS || PRECALCULUS

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
3D IntersectionGaussian EliminationEquation SolvingLinear AlgebraMath TutorialVariable EliminationAugmented Matrix3-Variable SystemsMathematical AnalysisEducational Content