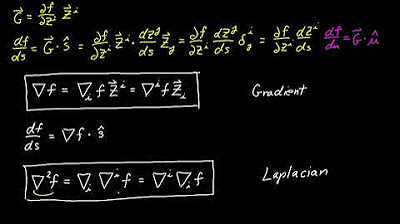Laplacian intuition
TLDRThis script delves into the concept of the Laplacian operator, a mathematical tool used in multivariable calculus. It explains the Laplacian as a second derivative that measures the 'concavity' of a function's graph, indicating whether a point is a local maximum or minimum. The script uses the gradient to describe the steepest ascent direction and the divergence to represent fluid flow, illustrating how the Laplacian can be visualized as water molecules converging or diverging from a point. It draws an analogy between the Laplacian and the second derivative in single-variable functions, promising an example in the next video.
Takeaways
- 📚 The Laplacian is an operator that acts on functions, similar to divergence, gradient, curl, or derivative.
- 📈 The Laplacian of a function F, denoted by a right-side-up triangle, produces a new scalar function of X and Y.
- 🔍 The Laplacian is defined as the divergence of the gradient of the function F, which is a second derivative in essence.
- 📉 The common notation for the Laplacian involves the dot product of the nabla operator with the gradient of F.
- 🧭 The gradient of a scalar function F gives a vector field representing the direction of steepest ascent.
- 🌊 The divergence of a vector field represents fluid flow, indicating where it converges or diverges.
- 🏞️ The Laplacian can be intuitively understood as a measure of whether a point is a local minimum or maximum by analyzing the gradient field.
- 🔺 Points of high divergence in the gradient field correspond to local minima where the function value is lower than its neighbors.
- 🔻 Conversely, points of low divergence or negative divergence correspond to local maxima or saddle points where the function value is higher than its neighbors.
- 📚 The Laplacian is analogous to the second derivative in single-variable calculus, indicating concavity and points of inflection.
- 🔍 The script suggests that the Laplacian can be used to determine the nature of critical points in multivariable functions.
Q & A
What is the Laplacian operator in the context of multivariable calculus?
-The Laplacian operator is a mathematical operator that acts on a scalar-valued function of multiple variables, such as two-dimensional space, and produces a scalar field. It is denoted by a right-side-up triangle and is defined as the divergence of the gradient of the function.
How is the Laplacian operator related to the gradient and divergence operators?
-The Laplacian operator is a second derivative because it is defined as the divergence of the gradient of a function. The gradient gives a vector field representing the direction of the steepest ascent, and the divergence of this vector field gives a scalar field, which is the Laplacian.
What does the gradient of a scalar-valued function represent?
-The gradient of a scalar-valued function represents the direction of the steepest ascent at a given point in the input space. It is a vector field where each vector points in the direction that maximizes the rate of increase of the function.
Can you explain the concept of divergence in the context of fluid flow?
-In the context of fluid flow, divergence represents the rate at which fluid is spreading out or converging at a point. A positive divergence indicates that fluid is moving away from a point, while a negative divergence indicates that fluid is converging towards a point.
How does the Laplacian operator help in understanding the nature of a point on a graph?
-The Laplacian operator helps in identifying whether a point on a graph is a local maximum, minimum, or saddle point. A high positive Laplacian indicates a local minimum, where the function value is lower than its neighbors, while a high negative Laplacian suggests a local maximum.
What is the intuitive meaning of the Laplacian operator in terms of a hill or valley on a graph?
-Intuitively, the Laplacian operator can be thought of as a measure of the 'depth' of a valley or the 'height' of a hill on a graph. At points where the graph is a valley (local minimum), the Laplacian is positive because the gradient vectors diverge away from that point. Conversely, at a hilltop (local maximum), the Laplacian is negative because the gradient vectors converge towards that point.
How is the Laplacian operator different from the second derivative in single-variable calculus?
-While both the Laplacian operator and the second derivative in single-variable calculus are measures of concavity, the Laplacian is an extension to functions of multiple variables. It provides information about the local behavior of a function in multidimensional space, whereas the second derivative is specific to functions of a single variable.
What is the common notation used to represent the Laplacian operator?
-The common notation for the Laplacian operator is an upside-down triangle, known as nabla, with a dot product notation, represented as '∇ · ∇F', where F is the scalar-valued function.
Why is the Laplacian operator important in the study of partial differential equations?
-The Laplacian operator is important in the study of partial differential equations because it describes the distribution of a physical quantity in a region, such as temperature or pressure, and is often used to model phenomena like heat conduction, fluid flow, and electrostatics.
Can the Laplacian operator be applied to functions of more than two variables?
-Yes, the Laplacian operator can be applied to functions of more than two variables. It generalizes to n-dimensional space, where it measures the rate of change of the function in all directions from a given point.
How does the Laplacian operator behave at points of inflection on a graph?
-At points of inflection on a graph, where the function changes concavity, the Laplacian operator is zero. This is because the gradient vectors neither diverge nor converge significantly at these points, indicating a balance between increasing and decreasing rates of change.
Outlines
📚 Introduction to the Laplacian Operator
The video script begins with an introduction to the Laplacian, a mathematical operator that acts on functions to produce another function. It is compared to other operators such as divergence, gradient, and curl. The Laplacian is specifically applied to multivariable functions, like one in two-dimensional space, denoted by F(X, Y), and its graph is visualized as a surface over the X-Y plane. The script explains that the Laplacian is represented by an upside-down triangle and it is defined as the divergence of the gradient of the function F, which is akin to a second derivative. The explanation includes a visual representation of the gradient as a vector field indicating the direction of steepest ascent or descent, and the divergence as a measure of fluid flow convergence or divergence. The Laplacian is then intuitively described as a tool to determine whether a point is a local minimum or maximum by examining the behavior of the gradient field around that point.
📉 The Laplacian as a Measure of Minimum and Maximum Points
This paragraph delves deeper into the Laplacian operator's role in identifying local minima and maxima of a function. It draws an analogy between the Laplacian and the second derivative in single-variable calculus, where a positive second derivative indicates a local minimum and a negative one indicates a local maximum. The script explains that the Laplacian operates similarly for multivariable functions, with high positive values at points that are local minima (where the function value is less than its neighbors) and high negative values at points that are local maxima (where the function value is greater than its neighbors). The paragraph concludes by setting up the expectation for a forthcoming example that will illustrate these concepts in action.
Mindmap
Keywords
💡Laplacian
💡Operator
💡Multivariable Function
💡Gradient
💡Divergence
💡Curl
💡Derivative
💡Scalar Valued Function
💡Nabla
💡Second Derivative
💡Critical Points
Highlights
The Laplacian is introduced as an operator similar to divergence, gradient, curl, and derivative.
It operates on a multivariable function, such as F(X, Y), to produce a new scalar function.
The Laplacian is denoted by an upside-down triangle and is defined as the divergence of the gradient of function F.
The common notation for the Laplacian involves the dot product of nabla with the gradient of F.
The gradient of a scalar function F gives a vector field representing the direction of steepest ascent.
The Laplacian can be understood intuitively through the concept of fluid flow and the divergence of the gradient field.
High divergence points indicate areas where vectors point away, suggesting a valley in the function's graph.
Low divergence points suggest areas where vectors converge, indicating a local maximum in the function's graph.
The Laplacian measures the 'depth' of a minimum point by comparing the function's value at a point to its neighbors.
A positive Laplacian indicates that the function's value at a point is less than its neighbors, suggesting a local maximum.
A negative Laplacian indicates that the function's value at a point is greater than its neighbors, suggesting a local minimum.
The Laplacian is analogous to the second derivative in single-variable calculus for multivariable functions.
The second derivative is negative at local maxima and positive at local minima, similar to the Laplacian's behavior.
The video promises to provide an example of the Laplacian in the next installment.
The Laplacian operator is a fundamental concept in understanding the behavior of scalar fields in multivariable calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: