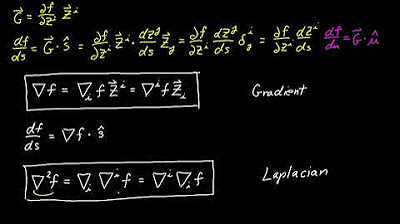Explicit Laplacian formula
TLDRThis video script introduces the concept of the Laplacian operator for multivariable functions with high-dimensional inputs. It explains how the Laplacian is derived from the divergence of the gradient vector field of a function, emphasizing its role in identifying maxima and minima. The script provides an alternative formula for the Laplacian using sigma notation, summing the second partial derivatives with respect to each variable. The explanation aims to clarify the computation of the Laplacian and its significance as an extension of the second derivative concept.
Takeaways
- 📚 The script discusses the concept of the Laplacian operator in the context of multivariable calculus with high dimensional inputs.
- 🔍 The Laplacian operator is explained as a way to transform a scalar-valued function into another scalar-valued function, akin to a second derivative.
- 📈 The gradient of a function f is introduced as a vector field obtained by taking partial derivatives with respect to each variable.
- 🌀 The divergence of the gradient vector field results in a scalar field, which is a key step in defining the Laplacian.
- 📝 An abstract formula for the gradient of f is provided, involving the del operator and partial derivatives for each variable.
- 🔢 The script outlines the process of calculating the Laplacian by taking the dot product of the del operator and the gradient vector.
- 📉 The Laplacian is expressed as the sum of second partial derivatives with respect to each variable, squared.
- 📚 The sigma notation is used to compactly represent the sum of the second partial derivatives for the Laplacian.
- 🧠 The script emphasizes the importance of understanding the Laplacian as an extension of the concept of a second derivative.
- 📑 The alternate formula for the Laplacian is presented as a more straightforward approach for computations.
- 🔍 The script concludes with a reminder of the Laplacian's role in identifying maxima and minima of a function, which was discussed in a previous video.
Q & A
What is a multivariable function in the context of the script?
-A multivariable function is a function that takes multiple inputs, represented as x1, x2, ..., xn, where n is a large number. It is a generalization of a single-variable function to more than one dimension.
What is the Laplacian operator in the context of calculus?
-The Laplacian operator is a differential operator that acts on a scalar-valued function to produce another scalar-valued function. It is defined as the divergence of the gradient of the function, effectively measuring the rate at which a function increases or decreases at a given point.
What does the gradient of a function represent?
-The gradient of a function is a vector field that points in the direction of the greatest rate of increase of the function and whose magnitude is the rate of that increase. It is found by taking the partial derivatives of the function with respect to each variable.
What is the relationship between the gradient and the Laplacian operator?
-The Laplacian operator is derived from the gradient. It takes the gradient, which is a vector field, and computes its divergence, resulting in a scalar field that represents the second derivative of the function in all directions.
How is the Laplacian operator represented in mathematical notation?
-The Laplacian operator is typically represented using the del operator (∇), which is a vector of partial differential operators. It is applied to the function to produce a scalar field that is the sum of the second partial derivatives of the function with respect to each variable.
What does the divergence of a vector field represent?
-The divergence of a vector field is a scalar field that represents the magnitude of a vector field's source or sink at each point. In the context of the Laplacian, it is the divergence of the gradient vector field.
What is the significance of the second partial derivative in the Laplacian formula?
-The second partial derivative in the Laplacian formula represents the curvature of the function in each variable's direction. Summing these up gives a measure of the overall curvature of the function in all directions.
How is the Laplacian of a function expressed using sigma notation?
-The Laplacian of a function is expressed using sigma notation as the sum from i=1 to n of the second partial derivatives of the function with respect to the i-th variable, written as ∑(i=1 to n) of ∂²f/∂xᵢ².
What is the intuition behind using the Laplacian operator to find maxima and minima of a function?
-The Laplacian operator can be used to identify points where the function has local maxima, minima, or saddle points. A positive Laplacian at a point indicates a local maximum, a negative Laplacian indicates a local minimum, and a zero Laplacian suggests a saddle point or that the test is inconclusive.
Is there an alternative way to think about the Laplacian operator, as mentioned in the script?
-Yes, the script suggests thinking about the Laplacian as taking the divergence of the gradient of a function. This perspective is helpful because the divergence is related to the concept of source and sink, which can be tied to the function's maxima and minima.
Why might the formula for the Laplacian be considered more straightforward for computations?
-The formula for the Laplacian, which sums the second partial derivatives with respect to each variable, is considered more straightforward for computations because it directly shows the components that need to be calculated without the need to first compute the gradient and then its divergence.
Outlines
📚 Understanding the Laplacian Operator for Multivariable Functions
This paragraph introduces the concept of the Laplacian operator in the context of multivariable functions with high dimensional inputs. It explains the Laplacian as a method to transform a scalar-valued function into another scalar function, which is akin to a second derivative. The explanation involves the gradient of the function, which is a vector field, and its divergence, resulting in a scalar field. The paragraph also presents an alternate formula for the Laplacian, emphasizing its computation through summing up the second partial derivatives with respect to each variable. The speaker corrects a minor error in the formula, highlighting the importance of the second derivative in understanding the Laplacian.
Mindmap
Keywords
💡Multivariable Function
💡Laplacian Operator
💡Gradient
💡Divergence
💡Partial Derivative
💡Second Derivative
💡Scalar Field
💡Sigma Notation
💡Maxima and Minima
💡Vector Full of Partial Differential Operators
💡Dot Product
Highlights
Introduction to multivariable functions with high dimensional inputs.
Explanation of the Laplacian operator for scalar valued functions.
The Laplacian as a second derivative-like measure obtained from the divergence of the gradient.
Visualization of the gradient of a function f as a vector field.
The divergence of the gradient vector field resulting in a scalar field.
Abstract representation of the gradient using the del operator and partial derivatives.
Multiplication of the del operator with the function f to obtain partial derivatives.
Description of the divergence process involving the dot product of the del operator and gradient vector.
Computing the second partial derivatives as part of the Laplacian formula.
Summation of second partial derivatives for the Laplacian in a compact sigma notation.
Generalization of the Laplacian formula for functions with three variables using x, y, z.
Mistake correction regarding the missing square in the second derivative notation.
Emphasis on the Laplacian as an extension of the second derivative concept.
Practicality of the Laplacian formula for computations in given examples.
Personal preference for conceptualizing the Laplacian as the divergence of the gradient of f.
Connection between the divergence and the maxima/minima of the original function.
Anticipation of the next video in the series.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: