Gradient and graphs

Khan Academy
11 May 201606:10
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script explores the concept of the gradient in the context of function graphs. It explains the gradient as an operator that transforms a function into a vector field, illustrating the direction and steepness of the steepest ascent on the graph. The script uses the example of the function f(x, y) = x^2 + y^2 to demonstrate how the gradient vector field points away from the origin, representing the direction of maximum increase in altitude. It also hints at the importance of the directional derivative in understanding why the gradient vector provides the steepest ascent direction, promising a deeper explanation in the next video.

Takeaways
  • 📚 The gradient of a function is a vector operator that takes a function and outputs another function with vector values.
  • 📉 The gradient is represented by the upside-down triangle and consists of the partial derivatives with respect to x and y.
  • 🔍 For a function like f(x, y) = x^2 + y^2, the gradient is (2x, 2y), indicating the rate of change in each direction.
  • 🌐 The gradient can be visualized as a vector field, showing vectors at each point in the xy-plane.
  • 🏔 The vectors in the vector field point away from the origin, representing the direction of the steepest ascent on the graph of the function.
  • 🚶‍♂️ Imagining walking along the graph, the gradient vector at any point shows the direction to walk to increase altitude the fastest.
  • 📈 The direction of the gradient vector is the direction of steepest ascent, which is useful for understanding the steepness of the function's graph.
  • 🌈 The length of the gradient vector indicates the steepness of the slope at a given point on the graph.
  • 📊 The color in the vector field represents the length of the vectors, with red indicating longer vectors and blue indicating shorter ones.
  • 🧭 The gradient field, or the vector field representing the gradient, can guide towards peaks or valleys on the graph.
  • 🔬 Understanding the gradient requires the concept of the directional derivative, which will be explained in a subsequent video.
Q & A

  • What is the gradient in the context of a function's graph?

    -The gradient is an operator that takes a function and outputs another function with a vector-valued output. It is represented by the symbol ∇ and is composed of the partial derivatives of the original function with respect to each variable.

  • What does the gradient represent in terms of a two-dimensional input function?

    -For a function with a two-dimensional input, the gradient represents a vector field where each point in the input space (xy-plane) is associated with a vector that points in the direction of the steepest increase of the function's value at that point.

  • How is the gradient of the function f(x, y) = x^2 + y^2 evaluated?

    -The gradient of the function f(x, y) = x^2 + y^2 is evaluated by taking the partial derivatives with respect to x and y. The result is the vector (2x, 2y), where 2x is the partial derivative with respect to x and 2y is the partial derivative with respect to y.

  • What does the direction of the gradient vector indicate about the function's graph?

    -The direction of the gradient vector indicates the direction of steepest ascent on the function's graph. It points in the direction where the function's value increases most rapidly.

  • How does the length of the gradient vector relate to the steepness of the function's graph?

    -The length of the gradient vector is proportional to the steepness of the function's graph at that point. Longer vectors correspond to steeper slopes, indicating a more rapid increase in the function's value.

  • What is the significance of the color coding in the vector field representation of the gradient?

    -The color coding in the vector field representation of the gradient is used to indicate the length of the vectors. Typically, warmer colors like red represent longer vectors (steeper slopes), while cooler colors like blue represent shorter vectors (gentler slopes).

  • Can the gradient vector be visualized as a vector field?

    -Yes, the gradient vector can be visualized as a vector field, where each vector originates from a point on the input plane and points in the direction of the steepest ascent at that point.

  • What is the role of the partial derivative with respect to x in the gradient of f(x, y) = x^2 + y^2?

    -The partial derivative with respect to x in the gradient of f(x, y) = x^2 + y^2 is 2x. It represents the rate of change of the function with respect to x while treating y as a constant.

  • What is the role of the partial derivative with respect to y in the gradient of f(x, y) = x^2 + y^2?

    -The partial derivative with respect to y in the gradient of f(x, y) = x^2 + y^2 is 2y. It represents the rate of change of the function with respect to y while treating x as a constant.

  • How does the gradient help in understanding the behavior of a function's graph?

    -The gradient helps in understanding the behavior of a function's graph by providing information about the direction and rate of the steepest increase in the function's value at any given point.

  • What is the connection between the gradient and the directional derivative?

    -The connection between the gradient and the directional derivative will be explained in a subsequent video, but it involves the concept that the gradient vector points in the direction of the maximum rate of increase, which is related to the directional derivative.

Outlines
00:00
📚 Understanding the Gradient in Function Graphs

This paragraph introduces the concept of the gradient in the context of a function's graph. It explains that the gradient is an operator that takes a function with two-dimensional input and outputs a vector-valued function, represented by the partial derivatives with respect to x and y. The example of the function f(x, y) = x^2 + y^2 is used to illustrate how the gradient is calculated, resulting in a vector field that points away from the origin. The paragraph also hints at the practical application of the gradient as a direction of steepest ascent on the graph, likening it to a hiker seeking the quickest way to increase altitude on a mountain.

05:00
🔍 The Gradient's Role in Direction and Steepness

The second paragraph delves deeper into the implications of the gradient's direction and magnitude. It clarifies that the gradient vector points in the direction of steepest ascent on the graph of a function, using the analogy of walking uphill to understand this concept. The length of the gradient vector is also discussed, indicating the steepness of the slope at a particular point on the graph. The paragraph contrasts steep slopes represented by long, red vectors with shallow slopes indicated by short, blue vectors. It concludes by acknowledging the complexity of understanding why the gradient vector inherently represents the direction of steepest ascent and hints at the concept of the directional derivative, which will be explained in a future video.

Mindmap
Keywords
💡Gradient
The gradient, in the context of this video, refers to the derivative of a function with respect to its variables, represented as a vector. It is defined as an operator that takes a function and outputs another function with vector valued output, the components of which are the partial derivatives of the original function. The gradient is central to the video's theme as it helps visualize the direction of the steepest ascent on a graph of a function. For instance, the gradient of the function f(x, y) = x^2 + y^2 is discussed, and the video explains how the gradient points directly away from the origin, indicating the steepest direction of increase.
💡Function
A function, in mathematical terms, is a relation between a set of inputs and outputs such that each input is related to exactly one output. In the video, the function f(x, y) = x^2 + y^2 is used to illustrate the concept of the gradient. The function is crucial as it forms the basis for understanding how the gradient operates on a two-dimensional input to produce a one-dimensional output.
💡Partial Derivative
A partial derivative is the derivative of a function with respect to one of its variables, treating the other variables as constants. In the video, the partial derivatives with respect to x and y of the function f(x, y) are calculated to be 2x and 2y, respectively. These partial derivatives are integral to understanding the gradient vector, as they represent the rate of change of the function in each direction.
💡Vector Field
A vector field is a representation of a vector at every point in space. In the video, the gradient of the function is visualized as a vector field, where each vector represents the direction and magnitude of the steepest ascent at that point. The vector field is used to illustrate the concept of the gradient, showing how vectors point away from the origin for the given function.
💡Direction of Steepest Ascent
The direction of steepest ascent is the direction in which a function increases the fastest. The video explains that the gradient vector points in this direction. For the function f(x, y) = x^2 + y^2, the gradient vectors point directly away from the origin, indicating that moving away from the origin in any direction will increase the function's value most rapidly.
💡Operator
In the context of the video, an operator is a mathematical process that takes one function and produces another function. The gradient is described as an operator that outputs a vector-valued function from a given function. The concept is used to explain how the gradient is derived from the original function by taking its partial derivatives.
💡Derivative
A derivative in calculus is a measure of how a function changes as its input changes. In the video, derivatives are taken with respect to x and y to find the partial derivatives, which are then used to form the gradient vector. The derivative is fundamental to understanding the rate of change of the function and its relation to the gradient.
💡Constant
In calculus, a constant is a value that does not change. In the context of taking partial derivatives, if a term in a function is treated as a constant with respect to a particular variable, its derivative with respect to that variable is zero. The video uses this concept to explain why the partial derivative with respect to y of x^2 is zero.
💡Variable
A variable in mathematics is a symbol that represents a value that can change. In the video, x and y are the variables of the function f(x, y). The concept of variables is essential for understanding how the gradient is calculated, as the partial derivatives are taken with respect to these variables.
💡Dimensional Input
Dimensional input refers to the number of independent variables a function accepts. The video mentions a two-dimensional input, which means the function f(x, y) takes two independent variables, x and y. This concept is important for understanding the multivariable nature of the function and how the gradient is derived from it.
💡Vector
A vector is a quantity that has both magnitude and direction. In the video, the gradient is described as a vector that gives the direction of the steepest ascent. The concept of a vector is crucial for visualizing the gradient as it provides a way to represent the rate and direction of change of the function.
Highlights

The gradient is explained in the context of a function's graph, illustrating its meaning and application.

A function f(x, y) = x^2 + y^2 is used as an example to demonstrate the concept of gradient.

Gradient is defined as an operator that outputs another function with vector valued output based on partial derivatives.

The partial derivatives with respect to x and y are calculated for the given function example.

The gradient function is visualized as a vector field pointing away from the origin for the example function.

The concept of a vector field is introduced, with a reference to another video for further understanding.

The visualization of the gradient vector field is discussed, with an invitation for the viewer to predict its appearance.

The gradient vectors are described as pointing in the direction of steepest ascent for the function's graph.

A metaphor of a hiker on a mountain is used to explain the practical application of the gradient in finding the steepest ascent.

The gradient's direction is confirmed as pointing directly away from the origin for the given function example.

The length of the gradient vector is discussed as an indicator of the steepness of the slope.

Different colors in the vector field represent different lengths, with red indicating longer vectors.

The gradient field is shown in the context of another graph with negative values and multiple peaks.

The gradient vectors near the peak of the graph are described as pointing uphill, guiding towards the peak.

The concept of the directional derivative is hinted at as a key to understanding the gradient's direction and length.

A teaser for the next video is given, promising to clarify the connection between partial derivatives and the gradient's direction and length.

Transcripts

Browse More Related Video

Why the gradient is the direction of steepest ascent

Gradient and contour maps

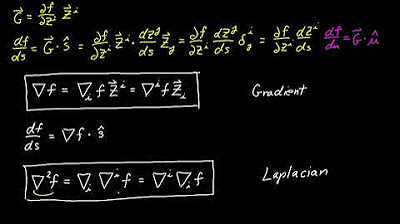
Video 39 - Gradient

Gradient 1 | Partial derivatives, gradient, divergence, curl | Multivariable Calculus | Khan Academy

Directional Derivatives (Calculus 3)

Tensor Calculus 13: Gradient vs "d" operator (exterior derivative/differential)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
GradientFunction GraphsPartial DerivativesVector FieldsSteepest AscentDirectional DerivativeMathematicsEducationalConceptualVisual Explanation