More on internal energy | Thermodynamics | Physics | Khan Academy
TLDRThis educational video script delves into the concept of internal energy, defining it as the total energy within a system, encompassing kinetic, potential, and bond energies of particles. It explains the conservation of internal energy, stating it cannot be created or destroyed but only transformed. The script clarifies misconceptions about heat and work, emphasizing their roles as energy transfers, not inherent properties of a system. Using the analogy of an energy 'bank account,' it illustrates how heat and work function as deposits and withdrawals, affecting the system's internal energy. The video aims to make viewers comfortable with determining when to use plus or minus for work in thermodynamic equations, employing practical examples and avoiding memorization.
Takeaways
- 🔑 Internal energy (U) is the total energy contained within a system, encompassing kinetic, potential, electrical, and bond energies of the particles.
- 📘 U is a state function, meaning its value depends only on the current state of the system, not the path taken to reach that state.
- 🚫 Internal energy cannot be created or destroyed; it can only be transformed from one form to another within the system.
- ♨️ Heat is not a property of the system but a process of energy transfer; it's not measured as a state variable like internal energy, pressure, or volume.
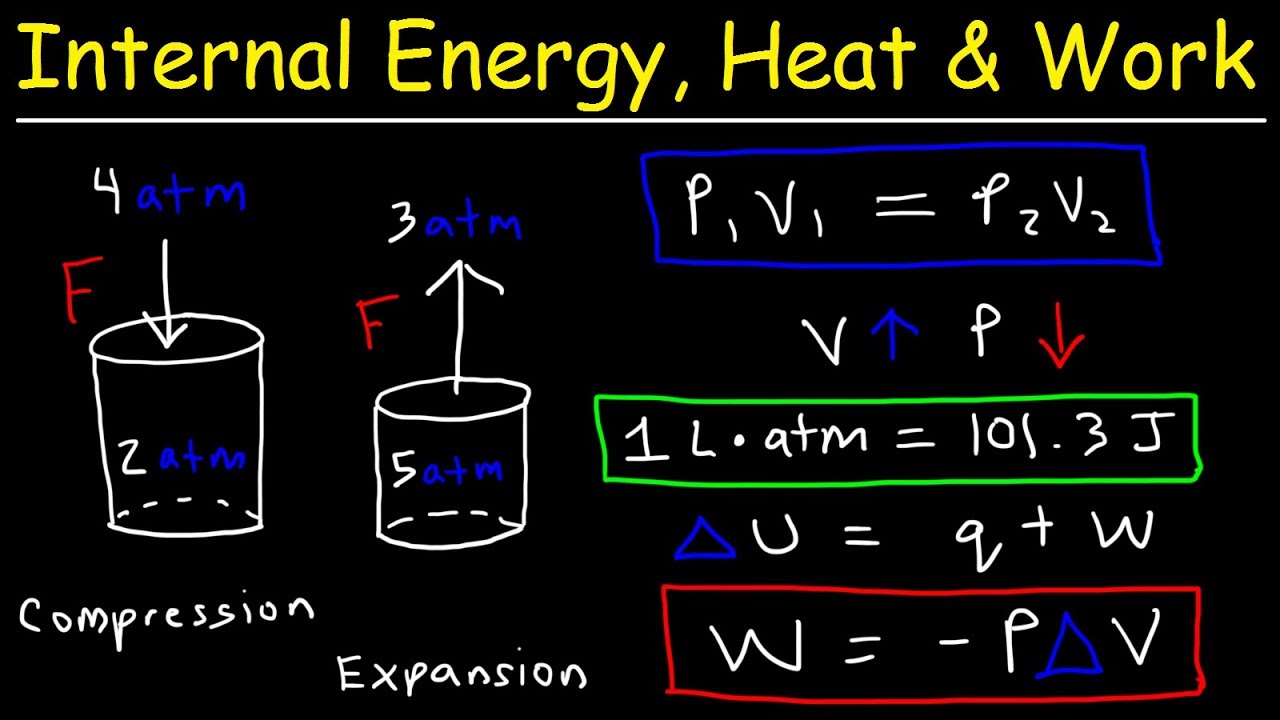
- 💡 The change in internal energy (ΔU) can be calculated by the heat added to the system (Q) plus the work done on the system (W), or alternatively, Q minus the work done by the system.
- 💡 The script emphasizes that heat is not an inherent property of a system but a transfer that occurs, similar to a deposit or withdrawal in a bank account.
- 🔄 The analogy of a bank account is used to illustrate the concept of internal energy, where heat and work are considered as energy deposits or withdrawals.
- 🔄 It's incorrect to say there is a certain amount of heat or work 'in' the system; rather, these are processes that change the system's internal energy.
- 🤔 The script suggests avoiding confusion by not treating heat and work as state variables, and instead focusing on their roles as energy transfers.
- 📚 The importance of understanding when to use plus or minus for work in calculations is highlighted, with the suggestion to rely on conceptual understanding rather than memorization.
- 📉 In a scenario where the system does work, it loses energy, and if work is done on the system, it gains energy, which affects the calculation of ΔU.
Q & A
What is internal energy?
-Internal energy is the total energy contained within a system, which includes the sum of kinetic and potential energies of all particles, as well as the energy associated with chemical bonds and electrical potentials.
Why is the symbol 'U' used to represent internal energy?
-The symbol 'U' is used to represent internal energy, and while it might seem unintuitive, the speaker suggests that it could be thought of as containing the 'universe of energy' as a mnemonic for memorization.
How is the internal energy of a system related to its state?
-The internal energy of a system is a function of its state. Knowing the state variables such as pressure, volume, and temperature, along with the type of molecule, allows one to determine the system's internal energy.
What is the principle behind the conservation of internal energy?
-The principle of conservation of internal energy states that internal energy cannot be created or destroyed randomly; it can only be transformed from one form to another within a system.
What are the two primary ways in which internal energy can change in a simple system?
-In a simple system, such as one dealing with gases, the change in internal energy can primarily be due to heat added to the system and work done on the system.
Why does the speaker avoid using the term 'delta' when discussing changes in internal energy?
-The speaker avoids using 'delta' to clarify that heat and work are not inherent states of the system but rather transfers of energy, similar to deposits or withdrawals in a bank account.
What is the difference between heat and temperature in the context of thermodynamics?
-In thermodynamics, heat refers to the transfer of energy, whereas temperature is a measure of the average kinetic energy of particles in a system. They are not interchangeable, despite common language use.
How can the concept of a bank account be used to understand internal energy?
-The concept of a bank account can be used as an analogy for internal energy, where changes in the account represent changes in internal energy, and heat and work are like deposits and withdrawals that affect the account balance.
Why can't we say there is a certain amount of heat or work in a system?
-We can't say there is a certain amount of heat or work in a system because heat and work are processes, not properties. They describe energy transfer into or out of the system, not a static quantity within it.
What is the relationship between enthalpy and heat in a system?
-Enthalpy is a concept that measures the total heat content of a system. It is not directly discussed in the script, but it is mentioned as a future topic that will provide a way to understand how much heat is 'in' a system.
How can you determine the amount of heat added to a system if the internal energy and work done are known?
-If the change in internal energy (∆U) and the work done by the system (W) are known, the amount of heat added to the system (Q) can be determined using the formula ∆U = Q + W, where Q is the heat added if the system does work, or ∆U = Q - W if work is done on the system.
What is the net change in internal energy if 5 joules of heat are removed and 1 joule of work is done on the system?
-The net change in internal energy would be a decrease of 4 joules (∆U = -4 J), calculated by subtracting the heat removed (-5 J) from the work done on the system (+1 J).
Outlines
🔍 Internal Energy and Its Conservation
The first paragraph introduces the concept of internal energy as the total energy contained within a system, including kinetic and potential energies of particles, as well as energy from bonds and electrical potentials. It emphasizes that internal energy is a state function, meaning its value depends only on the current state of the system, not on how the system reached that state. The video also clarifies that internal energy, denoted by 'U', cannot be created or destroyed but can be transformed, and its change is related to heat added to the system and work done on it. The speaker introduces a personal mnemonic for 'U' and discusses the non-intuitive nature of heat and work in thermodynamics, comparing them to deposits and withdrawals in a bank account.
📚 Understanding Heat and Work in Thermodynamics
The second paragraph delves deeper into the relationship between heat, work, and internal energy. It challenges the common misconception that heat is a state variable of the system, explaining that heat is actually a transfer of energy. The speaker uses the analogy of a bank account to illustrate how heat and work act as deposits and withdrawals to the system's 'energy bank account'. The paragraph also addresses the confusion that can arise from different notations of the first law of thermodynamics, advocating for clarity in understanding that heat and work are not inherent properties of the system but rather processes that affect the system's internal energy.
🧩 Applying the First Law of Thermodynamics to Simple Problems
The third paragraph applies the concepts discussed to simple problems to build intuition about when to use plus or minus signs for work in thermodynamic equations. It uses the example of a balloon expanding and doing work on its surroundings to demonstrate how to calculate the heat added to the system when there is no change in internal energy. The speaker also presents alternative formulations of the first law of thermodynamics and shows that both lead to the same conclusion about the heat added to the system. The paragraph concludes with another example involving heat removal and work done on the system, reinforcing the idea that changes in internal energy are the result of energy transfers in the form of heat and work.
Mindmap
Keywords
💡Internal Energy
💡System
💡Kinetic Energy
💡Potential Energy
💡Electrical Potential Energy
💡Chemical Bonds
💡Heat
💡Work
💡First Law of Thermodynamics
💡State Variables
💡Enthalpy
Highlights
Internal energy is defined as the sum of all energy within a system, including kinetic, potential, electrical, and bond energies.
The symbol 'U' stands for internal energy, with a mnemonic that it contains the 'universe of energy'.
Internal energy is a state function, determined by the system's state like pressure, volume, and temperature.
The principle of conservation of energy applies to internal energy, meaning it cannot be created or destroyed, only transformed.
A change in internal energy can be represented by the equation ΔU = Q + W, where Q is heat and W is work done on the system.
Heat is not a property of the system but a process of energy transfer, unlike internal energy, pressure, and volume which are state variables.
The concept of heat as a transfer is likened to a wire transfer in a bank account, emphasizing its role in changing internal energy.
Work done by the system results in a loss of energy, while work done on the system results in a gain.
The video clarifies the difference between 'work done by the system' and 'work done on the system' in the context of energy changes.
An example problem demonstrates how to calculate the heat added to a system when there is no change in internal energy and work is done.
The formula ΔU = Q + W is used to illustrate the calculation of heat and work in relation to a system's internal energy change.
An alternative formula ΔU = Q - W is presented to show different ways of expressing the relationship between heat, work, and internal energy.
A second example problem is solved to show the calculation of internal energy change when heat is removed and work is done on the system.
The importance of understanding the intuitive concepts behind the formulas rather than just memorizing them is emphasized for problem-solving.
The video aims to make viewers comfortable with determining when to use plus or minus for work in thermodynamics problems.
The concept of enthalpy as a way to measure heat in a system is briefly mentioned as a topic for a future video.
The video concludes with a summary of the intuitive approach to understanding heat and work in relation to internal energy changes.
Transcripts
Browse More Related Video

First law of thermodynamics / internal energy | Thermodynamics | Physics | Khan Academy

First Law of Thermodynamics, Basic Introduction - Internal Energy, Heat and Work - Chemistry

Enthalpy | Thermodynamics
Internal Energy, Heat, and Work Thermodynamics, Pressure & Volume, Chemistry Problems

First Law of Thermodynamics, Basic Introduction, Physics Problems

Work and Energy
5.0 / 5 (0 votes)
Thanks for rating: