Differentiating Exponentials with Non-e Bases
TLDRIn this educational video, the presenter delves into the concept of derivatives of exponential functions, focusing on the natural base 'e' and its unique property where its derivative is the function itself. The script explains how to handle exponential functions with 'unnatural' bases by converting them into a natural base form using logarithms. It demonstrates the process of differentiating such functions using the chain rule and clarifies the mysterious 'm' constant that appears in the differentiation formula, ultimately revealing it to be 'log a'. The video aims to simplify the understanding of exponential differentiation and ensure that the rule works cohesively with previously learned concepts.
Takeaways
- 📚 The derivative of \( e^x \) is \( e^x \), where \( e \) is a special number approximately equal to 2.7.
- 🔍 The base \( e \) is known as the natural base because it simplifies calculus operations, especially when dealing with derivatives.
- 🔑 When the base of an exponential function is not \( e \), it is considered 'unnatural' and requires adjustment to find its derivative.
- 🤔 The speaker aims to find a constant multiplier for the derivative of an exponential function with an unnatural base.
- 📐 The process involves converting the problem into a more familiar form using logarithmic properties.
- 🧩 By taking the natural log of both sides of an equation \( y = a^x \), the base \( e \) can be introduced.
- 📉 The natural log law allows the exponent to be brought to the front as a coefficient, simplifying the differentiation process.
- 📈 After rewriting the exponential function with a natural base, the chain rule can be applied to find the derivative.
- 📝 The derivative of an exponential function with an unnatural base \( a^x \) is \( a^x \ln(a) \), where \( \ln(a) \) is the natural logarithm of the base.
- 🔄 The rule works in reverse as well; if you substitute \( e \) as the base, the natural logarithm simplifies to 1, confirming the original rule for \( e^x \).
- 📚 The final rule derived can be applied to all exponential functions, whether the base is natural or unnatural.
Q & A
What is the derivative of e to the power of x?
-The derivative of e to the power of x (e^x) is simply e to the power of x, or e^x itself.
Why is the base 'e' considered the natural base in calculus?
-The base 'e' is called the natural base because it is the unique base for which the derivative of the exponential function with that base is the function itself. This property makes 'e' particularly useful in calculus and natural logarithms.
What is the significance of the number 'e' in mathematics?
-The number 'e' is an important mathematical constant approximately equal to 2.71828. It is the base of the natural logarithm and is the limit of (1 + 1/n)^n as n approaches infinity. It appears in various mathematical fields, including calculus, complex analysis, and number theory.
What does the term 'unnatural basis' refer to in the context of exponential functions?
-In the context of exponential functions, 'unnatural basis' refers to any base other than 'e'. These bases do not have the property that their derivative is the function itself, making them less convenient for calculus operations.
How can you convert an exponential function with an unnatural base into a natural base?
-You can convert an exponential function with an unnatural base into a natural base by rewriting the function as e to the power of the natural logarithm of the original base, multiplied by the exponent. This process involves using logarithmic identities and properties.
What is the process of taking the natural logarithm of both sides of an equation?
-Taking the natural logarithm of both sides of an equation involves applying the natural logarithm function to each term in the equation. This process can simplify the equation and make it easier to solve or differentiate.
How does the chain rule apply to the differentiation of exponential functions with an unnatural base?
-The chain rule is used to differentiate composite functions. For an exponential function with an unnatural base, you would treat the base as a constant and differentiate the exponent (which is a function of x), then multiply by the derivative of the base with respect to x.
What is the derivative of an exponential function with an unnatural base, and how is it found?
-The derivative of an exponential function with an unnatural base 'a' raised to the power of 'x' is 'a^x' times the natural logarithm of 'a', or a^x * ln(a). This is found by rewriting the function with a natural base and applying the chain rule.
What is the role of the constant 'm' in the differentiation of exponential functions with an unnatural base?
-In the script, 'm' is used to represent the coefficient that comes out in front when differentiating an exponential function with an unnatural base. It is essentially the natural logarithm of the base 'a', or ln(a).
Can the rule for differentiating exponential functions with an unnatural base be applied to all exponential functions?
-Yes, the rule for differentiating exponential functions with an unnatural base can be applied to all exponential functions, regardless of whether the base is 'e' or any other number.
Outlines
📚 Introduction to Natural and Unnatural Bases in Calculus
The speaker introduces the concept of natural and unnatural bases in the context of calculus, focusing on the derivative of exponential functions. They explain that the derivative of e^x is simply e^x, where 'e' is a special number approximately equal to 2.7. This special number is known as the natural base because it simplifies the process of differentiation. The speaker also mentions that when dealing with exponential functions with bases other than 'e', the result is close but not exact, requiring a scaling factor. This leads to the concept of the natural base being essential for 'interesting calculus' and is the reason why the natural logarithm (ln) is used, which is a logarithm with base 'e'. The speaker then poses a question about finding the constant that appears when differentiating exponential functions with non-natural bases and suggests using logarithmic properties to tackle this problem.
🔍 Deriving the Derivative of Exponential Functions with Unnatural Bases
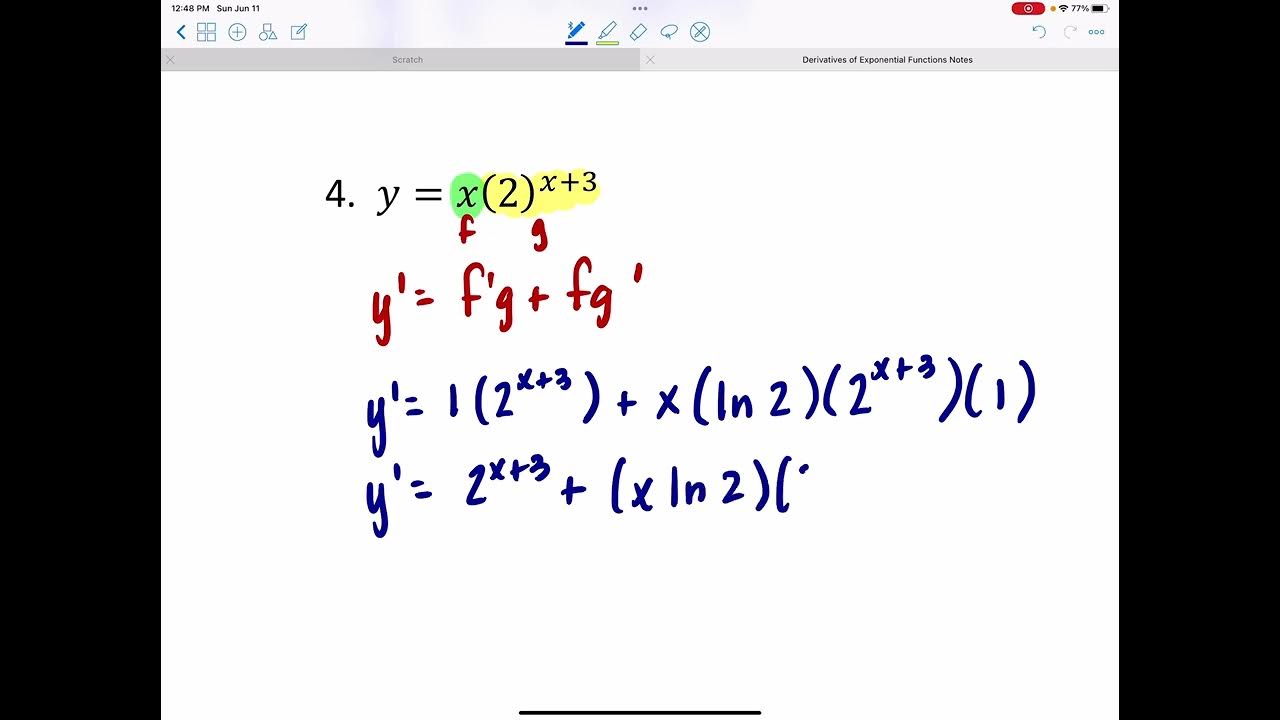
The speaker delves into the process of differentiating exponential functions with unnatural bases by converting them into a form that involves the natural base 'e'. They use logarithmic properties to rewrite the function y = a^x as e^(x * log(a)), which simplifies differentiation. By applying the chain rule, the derivative of y with respect to x is found to be a^x * log(a), where 'a' is the base of the original exponential function. This process is demonstrated step by step, with the speaker emphasizing the importance of understanding logarithmic laws and the chain rule in calculus. The speaker concludes by showing that this method works for all exponential functions, regardless of whether the base is 'e' or another number, and encourages the audience to apply this rule to various problems.
📝 Summary of Exponential Differentiation Rules
In the final paragraph, the speaker summarizes the differentiation rules for exponential functions, emphasizing that the rules apply to both natural and unnatural bases. They mention a specific problem, presumably question 77, which involves exponential functions with non-ideal bases. The speaker assures that the method discussed can be applied to these problems with a slight modification of the rule. They also suggest that the audience might want to highlight this rule for future reference, as it encompasses all exponential differentiation scenarios. The speaker concludes by inviting any questions from the audience, indicating the end of the explanation.
Mindmap
Keywords
💡Derivative
💡Natural Base
💡Unnatural Base
💡Exponential Function
💡Logarithm
💡Chain Rule
💡Logarithmic Identity
💡Differentiation
💡Inverse Functions
💡Coefficient
💡Desmos
Highlights
The derivative of e to the power of x (e^x) is e^x, highlighting the unique property of the natural exponential function.
Introduction of the concept of 'unnatural bases' for exponential functions, different from the natural base e.
Explanation of why the base e is considered 'natural' in calculus and its relation to natural logarithms.
The process of converting an 'unnatural base' exponential function into a natural base to simplify differentiation.
Use of logarithms to transform the base of an exponential function, leveraging the inverse relationship between exponentiation and logarithms.
Application of logarithmic identities to rewrite an exponential function with an unnatural base in terms of the natural base e.
The strategy of taking the natural logarithm of both sides of an equation to simplify the differentiation process.
Differentiation of an exponential function with an unnatural base using the chain rule, emphasizing the role of the logarithm of the base.
Identification of the constant 'm' in the derivative of an exponential function with a non-natural base, which is the logarithm of the base.
The generalization of the differentiation rule for exponential functions to include both natural and unnatural bases.
Demonstration of how the differentiation rule works with the natural base e, simplifying to e^x.
The test of a good mathematical rule is its consistency with previously learned concepts, as shown with the differentiation of e^x.
The differentiation rule for exponential functions with unnatural bases is a slight modification of the rule for natural bases.
The importance of understanding the differentiation of exponential functions with both natural and unnatural bases for solving calculus problems.
The transcript provides a comprehensive guide to differentiating exponential functions, making complex concepts more accessible.
The practical application of the differentiation rule for exponential functions in solving problem 77, which involves unnatural bases.
Encouragement for students to engage with the material, suggesting they may take over the process after understanding the foundational concepts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: