2.2 - Derivatives of Exponential Functions
TLDRThe video script offers an in-depth exploration of exponential functions, with a particular focus on the natural exponential function, denoted as 'e' to the power of 'x'. It explains that 'e' is a universal constant, approximately equal to 2.71, and is integral to various applications, including continuous compounding interest calculations. The script delves into the differentiation of exponential functions, highlighting that the derivative of 'e' to the power of 'x' is the function itself, a unique property that earns it the name 'natural'. It also covers how to apply differentiation rules such as the product, quotient, and chain rules to more complex functions involving 'e'. The video concludes with a real-world application, using the concept of 'e' to model and calculate the growth in spending on organic food and beverages in the United States, demonstrating the practical utility of exponential functions and their derivatives in applied mathematics.
Takeaways
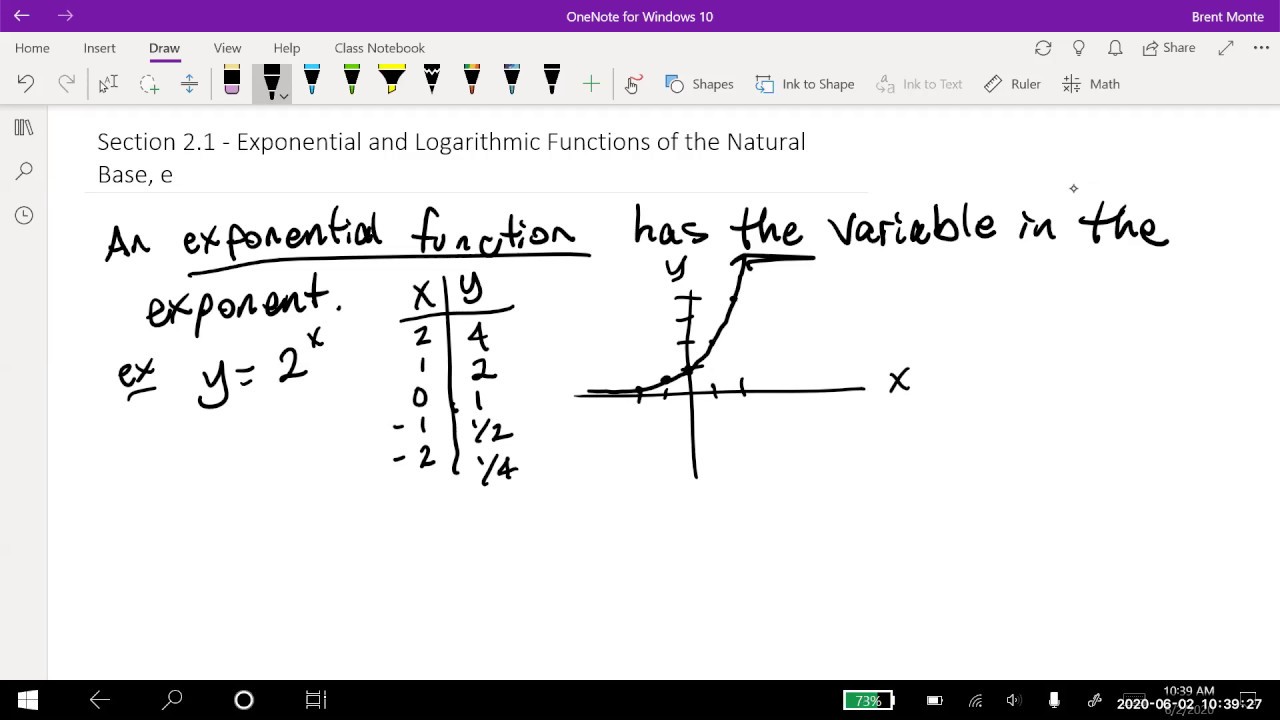
- 📚 The exponential function is defined as f(x) = a * b^(x), where a and b are constants, with b > 0, and the variable x is the exponent.
- 🌱 The natural exponential function is written as f(x) = e^(x), where e is a universal constant approximately equal to 2.71.
- 🔍 The constant e is found on calculators, often above the ln button, and can be accessed using the second function of the ln button.
- 🏦 e is particularly relevant in applications such as continuous compounding in finance, where the formula A = P * e^(r*t) is used to calculate account balances.
- 📈 The derivative of the natural exponential function e^(x) is itself, e^(x), which is a unique property and does not follow the power rule.
- ⚙️ When differentiating exponential functions, the power rule does not apply if the base is a constant and the exponent is the variable.
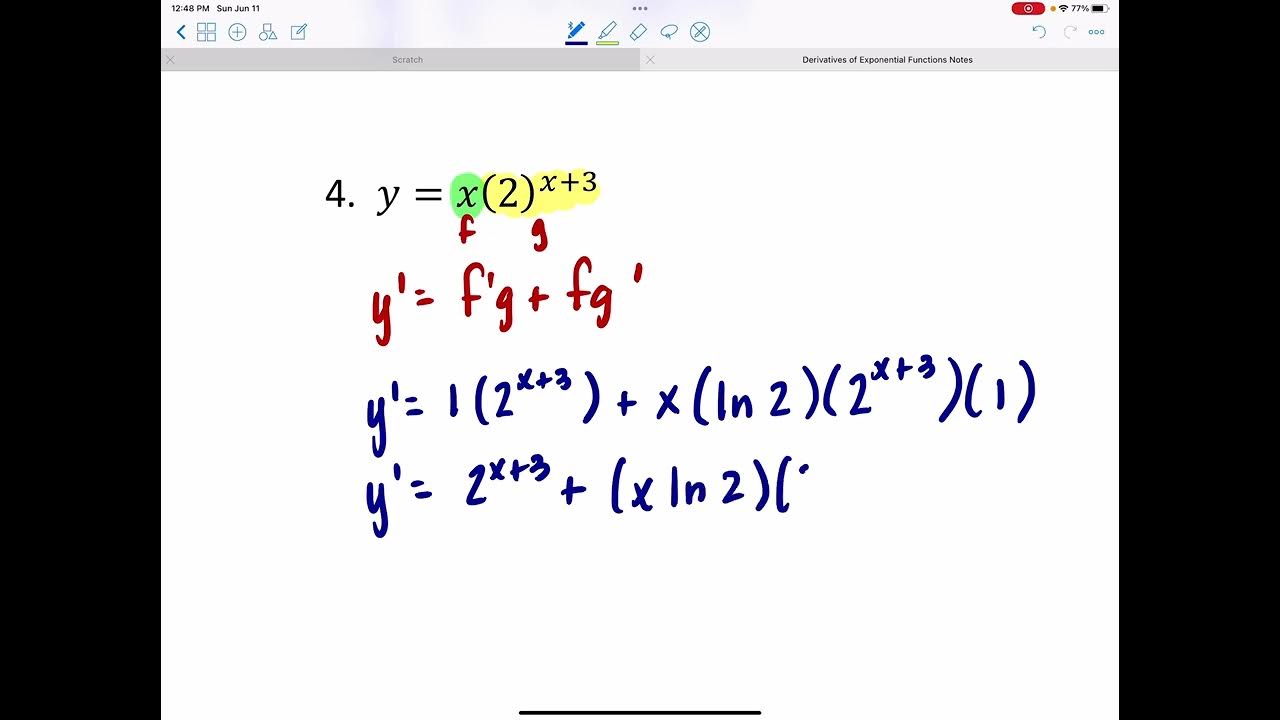
- 🤝 The product rule is applied when differentiating the product of a polynomial and an exponential function, combining the derivatives of both parts.
- 🔗 The quotient rule is used when differentiating a function that is the quotient of two functions, such as a polynomial divided by another polynomial.
- ⛓ The chain rule is essential for differentiating composite functions, especially when the exponent is another function of x.
- 📊 The function involving e can be used to model real-world phenomena, such as the growth in spending on organic food and beverages over time.
- ↗️ The rate of change of a function involving e, such as spending growth, is found by taking the derivative and evaluating it at a specific point in time.
Q & A
What is the general form of an exponential function?
-An exponential function is generally of the form f(x) = a * b^(x), where 'a' and 'b' are constants, and 'b' is greater than 0.
What is the natural exponential function?
-The natural exponential function is the function f(x) = e^(x), where 'e' is a universal constant, approximately equal to 2.71.
How is the constant 'e' accessed on a calculator?
-On a calculator, 'e' can be accessed by pressing the second function button and then the 'ln' button. It is also found above the division button, but without an exponent.
What is the significance of the number 'e' in the context of continuous compounding?
-The number 'e' is significant in continuous compounding as it is used in the formula to calculate an account balance subject to continuous interest compounding: A = P * e^(rt), where P is the principal, r is the interest rate, and t is the time in years.
What is the derivative of the natural exponential function e^x?
-The derivative of the natural exponential function e^x with respect to x is e^x, which means the function is its own derivative.
Why doesn't the power rule apply to the natural exponential function e^x when finding its derivative?
-The power rule doesn't apply to the natural exponential function e^x because in this case, the base is a fixed number (e) and the exponent is the variable (x), which is the opposite of the conditions under which the power rule is typically used.
How is the derivative of a function y = 3e^x calculated?
-The derivative of y = 3e^x with respect to x is 3e^x, since the derivative of e^x is e^x and the constant coefficient (3) remains unaffected by the differentiation.
What mathematical rule is used to differentiate a function that is a product of two other functions?
-The product rule is used to differentiate a function that is a product of two other functions. It states that the derivative of the product is the first function times the derivative of the second plus the second function times the derivative of the first.
What is the quotient rule used for in differentiation?
-The quotient rule is used to differentiate a function that is the quotient of two other functions. It states that the derivative of the quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator.
How is the chain rule applied when differentiating a function of the form e^(f(x))?
-The chain rule states that the derivative of e^(f(x)) is e^(f(x)) times the derivative of the inner function f(x). This is because the derivative of e to any power is e to that power, and you multiply by the derivative of the exponent.
In the context of the application problem involving organic food spending, what does the derivative of the spending function represent?
-The derivative of the spending function with respect to time represents the rate of change or the instantaneous growth rate of spending on organic food and beverages at a particular time.
Outlines
📚 Introduction to Exponential Functions
The video begins by introducing exponential functions, which are mathematical expressions where a constant base is raised to the power of a variable. The natural exponential function, denoted as e^x, is highlighted, with e being an irrational number approximately equal to 2.71. The video explains how to find e on a calculator and discusses its relevance in various applied contexts, such as continuous compounding in finance.
🔑 Derivative of Exponential Functions
The video then delves into the differentiation of exponential functions. It emphasizes that the derivative of e^x with respect to x is e^x itself, a unique property that does not apply the power rule. Several examples are provided to illustrate how to differentiate exponential functions, including those with constant coefficients, products of functions, and quotients. The importance of the product and quotient rules in these differentiations is also discussed.
📝 Factorization in Differentiation
The process of factorization is shown to be useful in simplifying derivatives of exponential functions. The video demonstrates how common factors, such as e^x, can be factored out from the derivative expressions. This technique is particularly helpful when applying the quotient rule, as it allows for the cancellation of terms and simplification of the final derivative form.
🔄 Application of Chain Rule
The video explains the application of the chain rule to exponential functions where the exponent is itself a function of x. It demonstrates how to differentiate composite functions involving e^x by taking the derivative of the outer function and multiplying it by the derivative of the inner function. Examples are provided to illustrate the process, including functions with quadratic and nested exponents.
🌱 Exponential Growth Application
An application involving the growth of spending on organic food and beverages in the United States is presented. The video shows how to use an exponential function to estimate the total amount spent in a given year and to calculate the rate of change of spending in another year. The process involves substituting the given year into the function and then differentiating the function to find the rate of change.
📉 Calculating the Rate of Change
The final part of the video focuses on calculating the rate of change of spending on organic food and beverages for the year 2018. It demonstrates how to find the derivative of the given exponential function and then evaluate it at the specific year. The rate of change is expressed in billions of dollars per year, providing insight into the growth trend of organic product spending.
Mindmap
Keywords
💡Exponential Function
💡Natural Exponential Function
💡Derivative
💡Continuous Compounding
💡Product Rule
💡Quotient Rule
💡Chain Rule
💡Irrational Number
💡Graphing Calculator
💡Organic Produce
💡Rate of Change
Highlights
An exponential function is defined as f(x) = a * b^x where a and b are constants and b > 0.
The base b in an exponential function is the fixed number, while the exponent is the variable x.
The natural exponential function is f(x) = e^x, where e is a universal constant approximately equal to 2.71.
The number e is used in various applied contexts, most importantly for continuous compounding.
The formula for continuous compounding is A = P * e^(r*t), where P is the principal, r is the interest rate, and t is time.
The derivative of the natural exponential function e^x is itself, e^x.
The power rule does not apply to exponential functions since the base is fixed and the exponent is the variable.
The derivative of a function of the form ce^x (where c is a constant) is simply c * e^x.
The product rule is used to differentiate a function that is a product of an exponential function and another function.
The quotient rule is applied when differentiating a function that is a quotient of two functions, one of which is exponential.
The chain rule is used to differentiate a function of the form e^(f(x)) where f(x) is another function of x.
When differentiating an exponential function using the chain rule, the derivative is e^(f(x)) times the derivative of f(x).
The number e is used to model growth processes, such as the increasing spending on organic food and beverages in the US.
The amount spent on organic food and beverages t years after 1995 can be modeled by the function A(t) = 2.43 * e^(0.8t).
To estimate the amount spent in a particular year, substitute the number of years after 1995 for t in the function.
To estimate the rate of spending growth in a particular year, find the derivative of the function with respect to t and evaluate at that year.
The derivative of an exponential function with base e is always the function itself, regardless of the exponent.
Transcripts
Browse More Related Video

Math1325 Lecture 11 2 - Derivatives of Exponential
Derivatives of Exponential Functions

Math 11 - Section 2.2

Business Calculus - Math 1329 - Section 4.3 - Derivatives of Exponential and Logarithmic Functions

What's so special about Euler's number e? | Chapter 5, Essence of calculus
Math 11 - Section 2.1
5.0 / 5 (0 votes)
Thanks for rating: