Multiplication & Addition Rule - Probability - Mutually Exclusive & Independent Events

The Organic Chemistry Tutor
31 Mar 201910:01
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains two fundamental rules of probability: the addition rule and the multiplication rule. The addition rule calculates the probability of event A or B occurring, while the multiplication rule calculates the probability of A and B occurring together. These rules are applied in an example where a student is deciding between taking algebra and biology courses. The probability of taking both or either course is calculated using the formulas. It's determined the events are not independent or mutually exclusive based on the probability values. The summary highlights key takeaways about calculating probability using these two important rules.

Takeaways
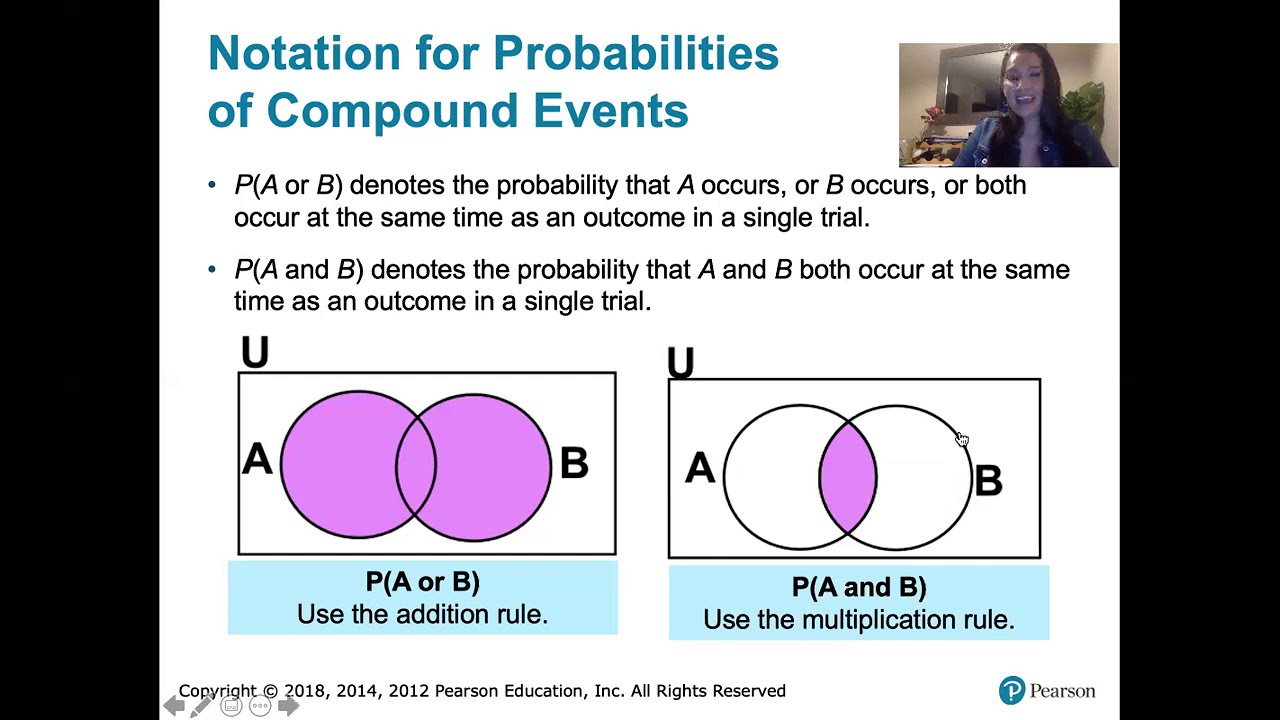
  • 😀 The addition rule: P(A or B) = P(A) + P(B) - P(A and B)
  • 😎 The multiplication rule: P(A and B) = P(A given B) * P(B)
  • 🤓 Conditional probability: P(A given B) = P(A and B) / P(B)
  • 🧐 If A and B are independent events, P(A and B) = P(A) * P(B)
  • 👍 Order doesn't matter for P(A and B) vs P(B and A)
  • 📝 Use addition rule if given P(A), P(B), P(A and B)
  • 📚 Use multiplication rule if given P(A given B) and P(B)
  • 😉 Events are independent if P(A given B) = P(A)
  • ❌ Events are mutually exclusive if P(A and B) = 0
  • 📈 Apply formulas to calculate probabilities of combined events
Q & A

  • What is the formula for calculating the probability of event A or event B occurring?

    -The formula is P(A or B) = P(A) + P(B) - P(A and B).

  • When can you use the simplified formula P(A or B) = P(A) + P(B)?

    -You can use the simplified formula when A and B are mutually exclusive events, meaning they cannot occur at the same time.

  • What is conditional probability?

    -Conditional probability is the probability of one event occurring given that another event has already occurred. It is calculated as P(A given B) = P(A and B) / P(B).

  • How are the formulas P(A and B) = P(A given B)*P(B) and P(A and B) = P(B given A)*P(A) related?

    -These two formulas are related because P(A and B) is the same regardless of order. They allow you to calculate P(A and B) if given information about conditional probabilities.

  • When can you use the formula P(A and B) = P(A)*P(B)?

    -You can use this formula when A and B are independent events. In that case, the occurrence of one event does not affect the probability of the other event.

  • In the example, are enrolling in algebra and enrolling in biology independent events?

    -No, they are not independent because P(algebra given biology) does not equal P(algebra). The probability of taking one course affects the probability of taking the other.

  • In the example, what is the probability Sarah enrolls in both algebra and biology?

    -The probability she enrolls in both is 0.28 or 28%.

  • In the example, are algebra and biology mutually exclusive events?

    -No, they are not mutually exclusive because the probability of Sarah taking both courses is not 0. She can take both courses.

  • What does order not being relevant for P(A and B) mean?

    -It means that P(A and B) = P(B and A) because the events occur simultaneously, so which event is labeled A and which is B does not matter.

  • What information is needed to determine if two events A and B are independent?

    -You need to know P(A), P(B), and P(A given B). If P(A given B) equals P(A), then A and B are independent events.

Outlines
00:00
😊 Addition and Multiplication Rules of Probability

This paragraph explains two basic rules of probability - the addition rule and the multiplication rule. The addition rule states that the probability of A or B occurring is the probability of A plus the probability of B minus the probability of A and B together. The multiplication rule relates to conditional probability - the probability of A and B occurring is the probability of A given B times the probability of B. These rules apply regardless of whether events are independent or mutually exclusive.

05:02
😃 Applying Probability Rules to Course Enrollment Scenario

This paragraph applies the probability rules to a scenario where Sarah is deciding which college courses to enroll in. Given probabilities related to enrolling in algebra and biology, calculations are done to determine: the probability she takes both courses, the probability she takes algebra or biology, whether the events are independent, and whether they are mutually exclusive.

Mindmap
Keywords
💡Addition Rule
The addition rule in probability refers to a method for calculating the probability of either of two events happening. It states that the probability of event A or event B occurring is equal to the sum of the probabilities of each event occurring separately, minus the probability of both events occurring together. This rule is crucial for understanding how to combine probabilities of events, especially when they have a chance of happening simultaneously. In the script, it's explained that for mutually exclusive events, where the events cannot happen at the same time, this formula simplifies to just the sum of the probabilities of each event, as the overlap is zero.
💡Mutually Exclusive Events
Mutually exclusive events are events that cannot occur at the same time. In the context of probability, this means that the occurrence of one event precludes the occurrence of the other. The script mentions that for such events, the probability of A and B occurring together is zero. This concept is important for applying the correct version of the addition rule, as it simplifies the formula to the sum of the probabilities of the events without needing to subtract the overlap, since there is none.
💡Multiplication Rule
The multiplication rule is used to find the probability of two events happening together. It involves multiplying the probability of one event by the probability of a second event occurring given that the first event has already occurred. This rule is foundational for understanding dependent events in probability, where the outcome or occurrence of one event affects the likelihood of another. The script explains how this rule can be applied using conditional probabilities, illustrating the interconnected nature of events in certain scenarios.
💡Conditional Probability
Conditional probability is the likelihood of an event occurring given that another event has already occurred. This concept is central to the script's discussion on the multiplication rule, illustrating how the probability of event A given event B (notated as P(A|B)) is calculated. Conditional probability is used to adjust the probability of an event based on new information that another event has occurred, reflecting a more refined approach to assessing probabilities in interconnected scenarios.
💡Independent Events
Independent events are two or more events where the occurrence of one event does not affect the probability of the other event(s). The script mentions that for independent events, the probability of A given B is simply the probability of A, as its occurrence is not influenced by B, and vice versa. This concept is crucial for determining when the simple multiplication of probabilities is applicable, streamlining the calculation for the probability of both events occurring together without needing to consider any conditional aspects.
💡Probability
Probability measures the likelihood of an event occurring, ranging from 0 (impossible event) to 1 (certain event). It is a fundamental concept throughout the script, used to assess the chance of various academic course enrollments. Understanding probability is essential for applying both the addition and multiplication rules, as well as for interpreting conditional probabilities and distinguishing between independent and mutually exclusive events.
💡Event
An event in probability is an outcome or a set of outcomes from an experiment. The script discusses various events, such as enrolling in algebra or biology courses, to illustrate how probabilities are calculated and combined. Events are the basic units of probability theory, and understanding their interactions is key to applying probability rules correctly.
💡Overlap
Overlap refers to a situation where two events can occur at the same time. In the context of the addition rule, the probability of the overlap (event A and event B occurring together) needs to be subtracted from the sum of the individual probabilities to avoid double-counting. The concept of overlap is crucial for accurately calculating the combined probability of two events.
💡Equation Rearrangement
Equation rearrangement is a mathematical technique used to manipulate formulas to isolate a desired variable. The script demonstrates this technique in the context of solving for the probability of two events occurring together, showing how equations can be rearranged to express the joint probability in terms of conditional probabilities. This skill is vital for effectively applying probability rules and understanding the relationships between different probability measures.
💡Joint Probability
Joint probability refers to the probability of two or more events happening at the same time. It is a key concept in the script when discussing the multiplication rule and independent events, as it involves calculating the likelihood of event A and event B occurring together. Understanding joint probability is essential for analyzing scenarios where multiple outcomes are of interest, and it underpins the calculation of both dependent and independent event probabilities.
Highlights

First significant highlight text

Second notable highlight text

Transcripts

Browse More Related Video

4.2.1 Addition and Multiplication Rules - Simple and Compound Events, and Their Probabilities

Probability Formulas, Symbols & Notations - Marginal, Joint, & Conditional Probabilities

AP Stats Test Quick Review: Probability

Elementary Stats Lesson #8

4.2.5.1 Addition and Multiplication Rules - The Rationale Behind the Multiplication Rule

4.2.2 Addition and Multiplication Rules - The Addition Rule

Rate This

5.0 / 5 (0 votes)

Thanks for rating: