2.3 - Derivatives of Logarithmic Functions
TLDRThe video script delves into the mathematical concepts of exponential and logarithmic functions, focusing on their differentiation. It explains that the exponential function e^x is unique as its derivative is the function itself. Logarithmic functions are presented as the inverse of exponentials, with the logarithm base 10 of a number being the exponent required to reach that number with 10 as the base. The script illustrates how to convert logarithmic expressions into exponential form and introduces key properties of logarithms that facilitate the simplification of complex expressions. These properties include the behavior of logarithms with respect to multiplication, division, and exponentiation, as well as the special case of the natural logarithm (ln), which is the logarithm with the base e, a mathematical constant. The script also demonstrates how to differentiate logarithmic functions, including the use of the chain rule and quotient rule, and applies these concepts to solve for maximum profit in a business context. The summary underscores the practical applications of these mathematical principles in real-world scenarios.
Takeaways
- 📈 The exponential function e^x is unique because it is its own derivative, meaning the derivative of e^x is also e^x.
- 🔗 Logarithmic functions are the inverse of exponential functions, and they are used to solve for exponents in equations where the base is fixed and the exponent is variable.
- ↔️ The relationship between exponential and logarithmic functions can be converted into one another, which helps in understanding and solving problems.
- ⚖️ Logarithms have properties that allow for the simplification of expressions, such as the product rule (log(a*b) = log(a) + log(b)) and the quotient rule (log(a/b) = log(a) - log(b)).
- 📚 The natural logarithm (ln) is the logarithm with the base e, and it is commonly used in calculus and various real-world applications.
- 🔑 The derivative of the natural logarithm function ln(x) with respect to x is 1/x, which is a direct rule used in calculus.
- 📌 Logarithms can be used to solve equations involving exponentials by applying the inverse property, which cancels out the exponential base, leaving the exponent.
- 🔢 The natural logarithm of a number can be found using a calculator's ln function, and it is often used to approximate values and find maximum or minimum values in applied problems.
- ⛏️ When differentiating functions involving natural logarithms, rules such as the product rule, quotient rule, and chain rule are applied based on the structure of the function.
- 🔍 To find maximum or minimum profit in an applied problem, set the derivative of the profit function to zero and solve for the critical points, then verify if these points correspond to maxima or minima by checking the sign of the derivative.
- 💡 Understanding the relationship between exponential and logarithmic functions, as well as the rules for their derivatives, is crucial for solving a wide range of mathematical and real-world problems.
Q & A
What is the unique property of the exponential function e^x that differentiates it from other exponential functions?
-The exponential function e^x is unique because it is its own derivative. This means that when you differentiate e^x, you get e^x itself.
How are exponential functions related to logarithmic functions?
-Exponential functions and logarithmic functions are closely related as they are inverses of each other. A logarithm is defined as the exponent to which a base must be raised to produce a given number, which is the operation that an exponential function performs.
What is the definition of a logarithm?
-A logarithm is defined as the inverse operation to exponentiation. It represents the exponent that makes an equation of the form 'base^exponent = number' true.
How can you convert a logarithmic expression to an exponential form?
-To convert a logarithmic expression to an exponential form, you switch the base of the logarithm with the base of the exponential, and swap the argument of the logarithm (the 'y' in log_b(y)) with the exponent of the exponential.
What is the natural logarithm?
-The natural logarithm is the logarithm with a base of 'e', where 'e' is a mathematical constant approximately equal to 2.71828. It is denoted as ln(x) and is widely used in calculus and various scientific fields.
What is the derivative of the natural logarithm of x with respect to x?
-The derivative of the natural logarithm of x, denoted as ln(x), with respect to x is 1/x.
How does the logarithm of a product relate to the sum of the logarithms of the individual factors?
-The logarithm of a product is equal to the sum of the logarithms of the individual factors. In other words, log_b(x*y) = log_b(x) + log_b(y).
What is the rule for differentiating a logarithmic function that is part of a larger product or quotient?
-When differentiating a logarithmic function that is part of a product or quotient, you would typically use the product rule or quotient rule respectively, combined with the standard derivative of the natural logarithm function, which is 1/x.
How can logarithms be used to solve equations involving exponentials?
-Logarithms can be used to solve equations involving exponentials by applying the logarithm with the same base to both sides of the equation. This cancels out the exponential, leaving you with the variable isolated as the exponent, which can then be solved for.
What is the significance of the natural logarithm in calculus?
-The natural logarithm is significant in calculus because it is the logarithm with a base of 'e', which is a fundamental number in mathematics. It is used extensively in calculus, especially when dealing with derivatives and integrals of exponential functions.
How can you find the marginal profit function from a given profit function?
-To find the marginal profit function, you take the derivative of the profit function with respect to the number of units sold. This derivative represents the rate of change of profit with respect to the number of units, which indicates the additional profit gained from selling one more unit.
Outlines
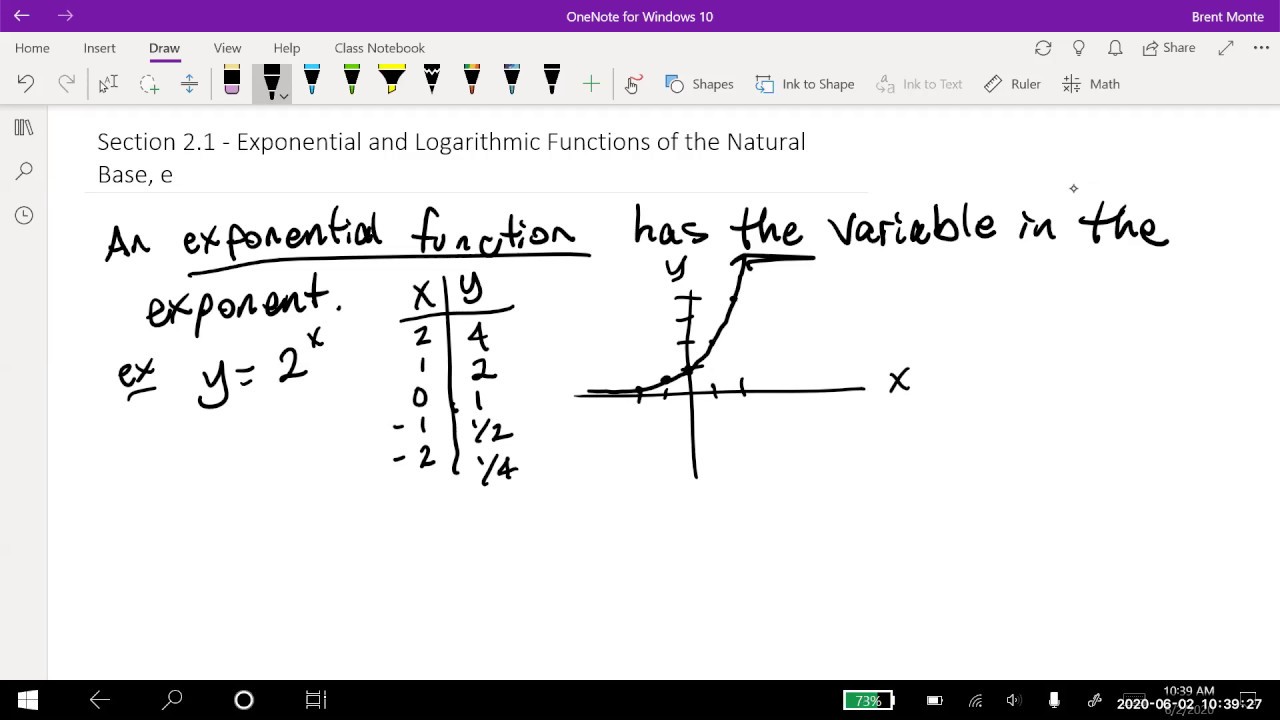
😀 Introduction to Logarithmic Functions
This paragraph introduces logarithmic functions as the inverse of exponential functions. It explains that the exponential function e^x is unique because its derivative is the same function. Logarithms are defined as the exponent to which the base must be raised to obtain a given number, with examples provided to illustrate this concept. The paragraph also clarifies the notation and terminology associated with logarithms.
🔗 Logarithms and Their Inverse Relationship with Exponentials
The second paragraph delves into the inverse relationship between logarithmic and exponential functions. It outlines how to convert logarithmic expressions into exponential form and vice versa. The process involves switching the base of the logarithm with the base of the exponential and swapping the positions of the other two numbers involved. The paragraph also provides examples to demonstrate the conversion process.
🔢 Solving Logarithmic Equations
This paragraph focuses on solving logarithmic equations by considering them as questions about exponents. It shows how to rewrite logarithmic expressions with variables in different positions, such as the base or the input, and how to solve for the unknown exponent. The paragraph also emphasizes the importance of understanding the definition of a logarithm and converting to exponential form when necessary.
📈 Special Properties of Logarithms
The fourth paragraph discusses the special properties of logarithms that help simplify expressions involving them. It covers the rules for logarithms of products and quotients, the effect of exponents within logarithms, and the inverse relationship between exponentials and logarithms of the same base. The paragraph also explains that the logarithm of one to any base is always zero and provides examples to illustrate these properties.
🔢 Logarithm Calculations and Limitations
This paragraph addresses the limitations of calculators when it comes to handling logarithms and emphasizes the importance of using logarithm rules to simplify expressions. It provides information on given logarithms, such as log base a of 2 and log base a of 3, and uses these to find the logarithm of 6 and the logarithm of 2/3, demonstrating how to apply logarithm rules to find values.
🤔 Creative Approaches to Logarithmic Problems
The sixth paragraph discusses the need for creativity when solving logarithmic problems that don't immediately relate to the given information. It explores alternative ways to express numbers, such as 81, using exponents and how logarithm rules can be applied to these expressions. The paragraph also covers the use of logarithm properties to find values like log base a of one-third and log base a of the square root of a.
📚 Logarithm Rules and Natural Logarithms
This paragraph introduces the concept of the natural logarithm, denoted as ln(x), which is the logarithm with base e. It explains that all the logarithm rules previously discussed also apply to the natural logarithm. The paragraph provides examples of how to simplify expressions involving natural logarithms using the given values for ln(2) and ln(3) and emphasizes the use of calculators for approximations.
🧮 Using Logarithms to Solve Exponential Equations
The eighth paragraph explains how logarithms can be used to solve equations involving exponentials. It demonstrates that applying a logarithm with the same base as the exponential can cancel out the exponential, leaving the exponent, which can then be solved for the variable. The paragraph provides examples of solving for x in e^x = 80 and e^t = 0.05, showing how to isolate the variable using logarithms.
📘 Defining and Simplifying Logarithmic Expressions
The ninth paragraph recaps the definition of a logarithm and the process of converting between logarithmic and exponential forms. It also discusses logarithm properties that allow for the simplification of expressions containing logarithms and introduces the concept of the natural logarithm. The paragraph concludes with a summary of the key points covered in the discussion about logarithms.
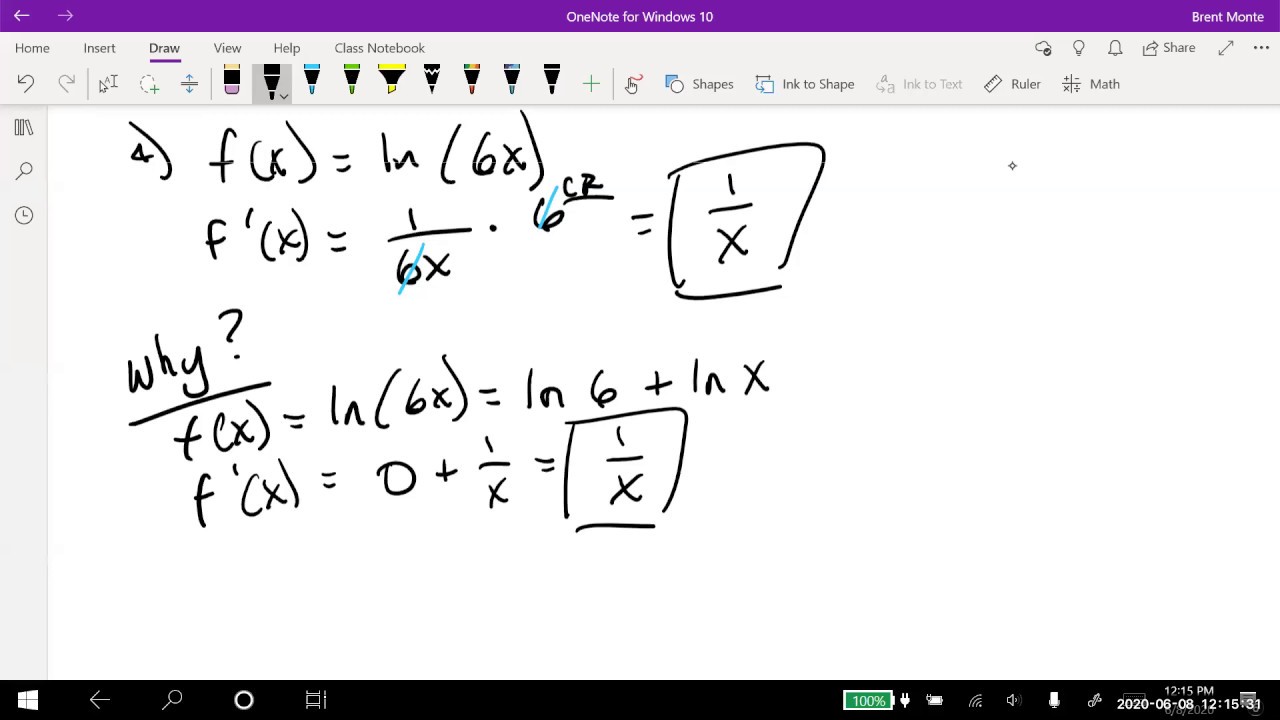
🔍 Derivative of Logarithmic Functions
The tenth paragraph focuses on the calculus aspect of logarithmic functions, specifically the derivative of the natural logarithm function. It explains that the derivative of ln(x) is 1/x and differentiates several functions involving natural logarithms, applying basic rules and the product rule. The paragraph also clarifies that the derivative of a natural logarithm function is not derived from the power rule.
🔗 Chain Rule and Logarithmic Differentiation
The eleventh paragraph explores the application of the chain rule when differentiating functions involving natural logarithms. It explains the process of differentiating the outer function (the natural log) and then multiplying by the derivative of the inner function. The paragraph provides examples of using the chain rule with natural logarithms and emphasizes the importance of not combining terms incorrectly due to the structure of logarithmic expressions.
🤔 Alternative Approaches to Differentiation
The twelfth paragraph presents an alternative approach to differentiating logarithmic functions by first applying logarithm rules to simplify the expression before differentiation. It contrasts this method with the direct application of the quotient rule and chain rule, showing that sometimes using logarithm rules can simplify the differentiation process, although it is not always necessary.
📈 Marginal Profit and Logarithmic Differentiation
The thirteenth paragraph applies the concept of logarithmic differentiation to an applied problem involving profit maximization. It demonstrates how to find the marginal profit function, evaluate it at a specific value, and use the derivative to determine the production level that maximizes profit. The paragraph concludes with a verification step to ensure that the critical value found corresponds to a maximum profit.
📉 Critical Values and Maximization
The fourteenth paragraph discusses the concept of critical values in the context of maximization and minimization. It explains how to find critical values by setting the derivative equal to zero and then verifying whether these points correspond to maxima or minima by examining the sign of the derivative around these points. The paragraph provides a step-by-step example of this process in the context of an applied problem.
📈 Exponential and Logarithmic Differentiation
The fifteenth paragraph summarizes the capabilities developed over the past two videos for differentiating exponential and logarithmic functions. It contrasts these functions with those that would require the power rule and emphasizes the expanded range of functions that can now be differentiated using these new rules.
Mindmap
Keywords
💡Exponential Function
💡Logarithmic Function
💡Derivative
💡Inverse Relationship
💡Base of a Logarithm
💡Natural Logarithm
💡Logarithm Rules
💡Exponential and Logarithmic Conversion
💡Chain Rule
💡Product Rule
💡Quotient Rule
Highlights
The exponential function e^x is unique because it is its own derivative.
Logarithmic functions are the inverse of exponential functions, defined as the exponent that satisfies a given equation of the form b^x = y.
The relationship between exponential and logarithmic functions can be visualized through the inverse relationship, where y = b^x is equivalent to x = log_b(y).
Logarithms can be used to solve equations of the form b^x = y by determining the exponent x that relates the base b to the number y.
The concept of logarithms can be simplified by converting them to their exponential equivalents, which may be more familiar to some learners.
The base of a logarithm is subscripted and represents the base of the exponential function that would result in the output value when raised to the power indicated by the logarithm.
Logarithms have special properties that allow for the simplification of expressions, such as the logarithm of a product being the sum of the individual logarithms.
The natural logarithm (ln) is the logarithm with the base e and is denoted as ln(x), where e is the mathematical constant approximately equal to 2.71828.
The rules of logarithms apply to the natural logarithm as well, including the ability to split products and quotients into sums and differences of logarithms, respectively.
The derivative of the natural logarithm of x (ln(x)) is 1/x, which is a distinct rule from the power rule and does not require the function to have an exponent of zero.
When differentiating a logarithmic function, the chain rule is applied when the logarithm is the outer function and another function is the input.
Logarithmic differentiation can be simplified by applying logarithm rules before differentiating, which can sometimes avoid complex algebraic steps.
Logarithms are used to solve equations involving exponentials by canceling out the exponential with the same base, leaving the exponent isolated.
The natural logarithm can be used to find the maximum or minimum values of profit functions in applied problems by setting the derivative equal to zero and solving for the critical points.
The derivative of a logarithmic function can be approximated using a calculator for practical applications, although the exact answer is an irrational number.
The quotient rule and chain rule are essential for differentiating more complex logarithmic functions involving quotients and other functions as inputs.
The natural logarithm is a fundamental tool in calculus, with broad applications in various scientific and mathematical fields, including the analysis of profit functions in economics.
The use of logarithms in differentiation can lead to cleaner and more understandable expressions, especially when dealing with products, quotients, and exponents within logarithmic functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: