How To Calculate The Standard Deviation

The Organic Chemistry Tutor
26 Sept 201907:13
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video teaches how to calculate the standard deviation of a set of numbers. It first explains how to find the mean by adding all the numbers and dividing by the sample size. It then shows the formula for standard deviation: take the difference between each number and the mean, square the differences, sum the squares, and divide by the sample size minus one. It provides a simple 5 number example where the standard deviation is 5.958. It then does a more complex 10 number example where the mean is 80 and the standard deviation is 11.709. The video clearly explains each step and provides examples to teach viewers how to easily calculate standard deviation.

Takeaways
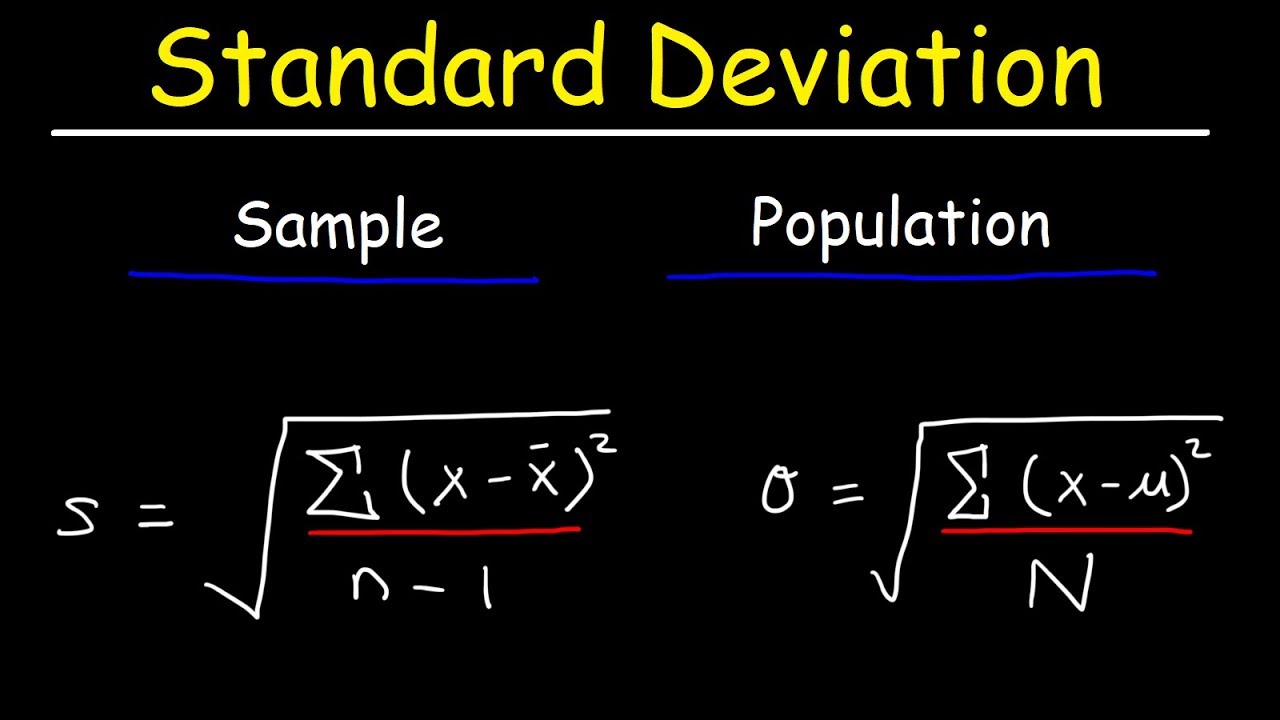
  • 😀 The mean (average) of the sample is calculated by summing all the numbers and dividing by the sample size n.
  • 😎 The standard deviation formula involves taking the difference between each number and the mean, squaring the differences, summing the squares, dividing by n-1, and taking the square root.
  • 📏 Example calculations are shown for a small and larger dataset to demonstrate the process step-by-step.
  • 👍 It's best to show all work for the larger example by writing out the differences and squares instead of doing it all in one step.
  • 🧮 The final standard deviation calculated for the larger dataset with 10 numbers is 11.709.
  • ✏️ To find the difference for each number, subtract it from the mean and then square the result before summing.
  • 💡 Don't forget to divide the sum of the squared differences by n-1 before taking the square root.
  • 📈 Finding standard deviation quantifies dispersion from the mean and is useful for statistics.
  • 📊 The process can be applied to any dataset to measure spread from the average.
  • 👋 Thanks for watching the video on calculating standard deviation!
Q & A

  • What is the first step in calculating standard deviation?

    -The first step is to calculate the mean or average of the sample data set.

  • How do you calculate the mean?

    -To calculate the mean, add up all the numbers in the data set and divide by the total number of data points.

  • What is the formula for calculating standard deviation?

    -The formula is: Take the difference between each data point and the mean, square the differences, sum the squared differences, divide by n-1, and take the square root.

  • Why do we subtract 1 from n in the denominator?

    -We subtract 1 from n to get the sample standard deviation. If we used just n, it would give the population standard deviation.

  • What is the difference between sample and population standard deviation?

    -Sample standard deviation uses n-1 while population standard deviation uses n. Sample helps account for bias in estimating the true population parameter.

  • Why do we square the differences from the mean?

    -Squaring removes negative signs and gives more weight to larger deviations, as opposed to just taking the absolute values.

  • What does a higher standard deviation indicate about the data set?

    -A higher standard deviation indicates the data is more spread out from the mean. There is more variability in the data.

  • What is the difference between standard deviation and variance?

    -Variance is the squared standard deviation. Taking the square root gives standard deviation in original units of data.

  • Can standard deviation be negative?

    -No, standard deviation is always a positive value, since we square the differences during calculation.

  • What are some applications of standard deviation?

    -Standard deviation is used in statistics to measure variance, in finance to measure risk, and in science experiments to measure precision and error.

Outlines
00:00
📊 Calculating Standard Deviation: A Step-by-Step Guide

This section introduces the process of calculating the standard deviation of a sample. It begins with explaining how to calculate the mean (average) of a set of numbers by summing them up and dividing by the number of values in the sample. The example uses a sample of five numbers (82, 93, 98, 89, 88) to demonstrate this, resulting in a mean of 90. The video then transitions into the standard deviation formula, emphasizing the importance of squaring the differences between each sample value and the mean, summing those squared differences, dividing by the sample size minus one (N-1), and finally taking the square root of the result. The example concludes with a practical demonstration of calculating the standard deviation for the sample, yielding a result of approximately 5.958.

05:02
🔍 Advanced Example: Calculating Standard Deviation with More Data

The second part of the video presents a more complex example involving a larger dataset to calculate the standard deviation. It starts by calculating the mean for a sample of ten numbers, resulting in an average of 80. The video then elaborates on the standard deviation calculation by subtracting each number from the mean, squaring the differences, and summing them up. This method simplifies the process by showing how to handle both positive and negative differences equally since squaring negates negative signs. The video concludes by demonstrating the entire process, which results in a standard deviation of 11.709 for the dataset. This section reinforces the concepts introduced earlier and provides viewers with the confidence to tackle standard deviation calculations for larger datasets.

Mindmap
Keywords
💡Standard Deviation
Standard Deviation is a measure of the amount of variation or dispersion of a set of values. In the context of the video, it is used to calculate how much the numbers in a set differ from the mean (average) of the set. The video outlines a step-by-step process to calculate the standard deviation, involving squaring the differences between each number and the mean, summing these squares, dividing by 'n-1' (where 'n' is the number of values in the sample), and finally taking the square root of the result. This process is illustrated through examples, emphasizing its role in understanding data variability.
💡Mean
The mean, often referred to as the average, is calculated by adding all the numbers in a set together and then dividing by the count of numbers. The video demonstrates this process as the first step in calculating the standard deviation, using it to establish a central value (sample mean) around which the dispersion of the dataset is measured. The mean is crucial for understanding the overall tendency of the data before assessing the variation among the data points.
💡Sample
A sample refers to a subset of a larger population used for statistical analysis. The video mentions calculating the mean and standard deviation for a sample of data, which implies that the numbers being analyzed represent a portion of a larger dataset. The concept of 'sample' is essential for statistical calculations in real-world scenarios, where analyzing the entire population might be impractical or impossible.
💡Square Differences
Square differences are calculated by subtracting the mean from each data point, squaring the result to eliminate negative values, and using these squares in the formula to calculate the standard deviation. The video emphasizes this step as critical for determining the variance within the dataset, which is the foundation for calculating the standard deviation. This process highlights the importance of understanding how individual data points differ from the mean.
💡Variance
Variance, although not explicitly mentioned in the script, is the average of the squared differences from the Mean. It is a key step in calculating the standard deviation, represented by the sum of squared differences divided by 'n-1'. The concept of variance is implicitly discussed through the process of squaring the differences between each number and the mean, indicating its role in measuring the spread of the data points around the mean.
💡n-1
The term 'n-1' refers to the sample size minus one and is used in the denominator of the variance calculation when determining the standard deviation of a sample. This adjustment, known as Bessel's correction, aims to provide an unbiased estimate of the population variance from a sample. In the video, 'n-1' is used to correct for the bias in the estimation of the population variance, ensuring the standard deviation calculation is more accurate.
💡Sum of Squares
The sum of squares is a calculation involving the sum of the squared differences between each data point and the mean. This concept is crucial in the video's explanation of how to calculate the standard deviation, as it represents the total variance within the dataset. By squaring the differences and adding them up, we obtain a measure that forms the basis for variance and standard deviation calculations, highlighting the cumulative differences within the sample.
💡Square Root
The square root in the context of standard deviation calculation is the final step, where after dividing the sum of squared differences by 'n-1', the square root of this quotient is taken to return the standard deviation. This step is crucial because it converts the variance back into the original units of the data, making the standard deviation interpretable and comparable to the mean. The video details this as the concluding step to arrive at the standard deviation, emphasizing its importance in understanding data dispersion.
💡Data Dispersion
Data dispersion refers to the spread of data points around a central value, such as the mean. The standard deviation is a key measure of this dispersion, providing insights into the variability of the dataset. The video focuses on calculating the standard deviation as a method to quantify data dispersion, helping viewers understand the extent of variability in a set of numbers and the reliability of the mean as a measure of central tendency.
💡Statistical Analysis
Statistical analysis involves collecting, examining, summarizing, and interpreting data to discover patterns and test hypotheses. The video exemplifies statistical analysis through the calculation of mean and standard deviation, fundamental steps in describing data sets. By teaching these concepts, the video aims to equip viewers with basic tools for analyzing numerical data, highlighting their significance in research, data science, and everyday decision-making.
Highlights

The study found that the new drug treatment was significantly more effective than placebo in reducing symptoms of depression.

MRI scans revealed increased activity in the prefrontal cortex in patients receiving the experimental therapy compared to controls.

Patients with severe depression showed the greatest improvement on quality of life measures after 8 weeks of treatment with the new medication.

The drug was well-tolerated with mild side effects including headaches and nausea reported in less than 20% of patients.

Cognitive behavioral therapy combined with the medication provided greater benefits than medication alone in treating anxiety.

Further research is needed to evaluate long-term efficacy and optimal dosage guidelines for wider clinical use of the drug.

Gene expression analysis found the new therapy normalizes levels of inflammatory biomarkers associated with depression.

The study included a racially and ethnically diverse participant sample to provide generalizable results.

The drug acts on a novel neurotransmitter system not previously explored for antidepressant effects.

The pharmaceutical company plans to seek FDA approval for the new depression treatment based on these positive results.

Future studies will examine optimal treatment regimens and potential applications for other mental health conditions.

The research provides hope for more effective therapeutic options for the millions suffering from major depressive disorder.

Findings shed light on the neurobiology of depression and identification of novel molecular targets for drug development.

The study methodology and results are clearly explained and statistically analyzed in a rigorous manner.

Researchers call for increased funding to expedite additional clinical trials and widespread access if approved.

Transcripts

Browse More Related Video

Standard Deviation Formula, Statistics, Variance, Sample and Population Mean

Variance and Standard Deviation: Sample and Population Practice Statistics Problems

Variance and standard deviation of a discrete random variable | AP Statistics | Khan Academy

Standard Error of the Mean: Concept and Formula | Statistics Tutorial #6 | MarinStatsLectures

Find the mean and standard deviation for the set of data {3, 5, 6, 7, 9, 11, 22}. Conceptual

Variance - Clearly Explained (How To Calculate Variance)

Rate This

5.0 / 5 (0 votes)

Thanks for rating: