Math1325 Lecture 11 2 - Derivatives of Exponential
TLDRThe video script is an educational discussion on the derivatives of exponential functions, focusing on the natural exponential function with Euler's constant as the base. It highlights the unique property that the derivative of e^x is the function itself. The script delves into applying the chain rule to exponential functions where the base is a function of x, using examples to illustrate the process. It also covers the product rule and quotient rule in the context of exponential functions. The application of exponential functions in financial growth is explored, specifically continuous compounding, with an example calculation of the future value of an investment and its growth rate. The script concludes with a look at exponential functions with bases other than e, discussing the derivative of a constant raised to the power of x and providing a formula for the derivative when the base is a constant and the exponent is a function of x.
Takeaways
- 📈 The derivative of the natural exponential function e^x is the same as the function itself, e^x.
- 🔗 For a composite exponential function f(u) = e^u where u is a function of x, the derivative is e^u times the derivative of u.
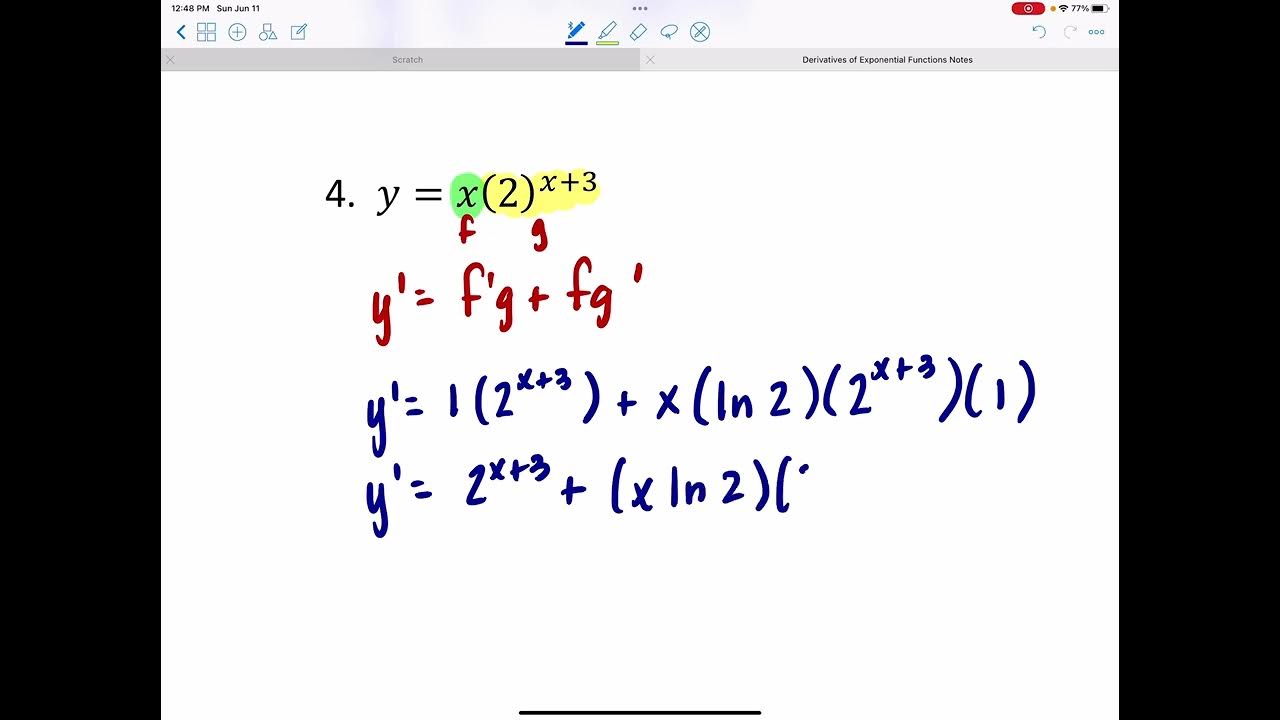
- 📚 The chain rule is applied when differentiating exponential functions with a variable base, such as e^(4x^3).
- ✅ The derivative of e^(4x^3) is 12x^2 * e^(4x^3), following the power rule and the chain rule.
- 🤝 The product rule is used when differentiating the function 3t * e^(3t^2 + 5t), combining the derivative of each part.
- 🧮 Simplifying the derivative of the product rule example yields 3t(60 + 5) * e^(3t^2 + 5t) after factoring out constants and the exponential term.
- 💡 The quotient rule is applied when differentiating a function with a numerator and denominator, such as e^(3w) / (3w^2 + 3w).
- 📊 The derivative of s(t) = 100e^(0.08t) gives the rate of growth of an investment, which is 8e^(0.08) dollars per year after one year.
- 🔑 For exponential functions with a base other than e, the derivative is a^x * ln(a) times the derivative of the exponent.
- 🌱 The derivative of a^x * ln(a) involves multiplying the exponential term by the natural logarithm of the base and the derivative of the exponent.
- 📌 The derivative of an exponential function with a base a and exponent u(x) is a^u * ln(a) * u'(x), showcasing the chain rule in action.
Q & A
What is the derivative of the natural exponential function e^x?
-The derivative of the natural exponential function e^x is the same as the function itself, which is e^x.
How does the derivative of an exponential function change when the exponent is a function of x?
-When the exponent is a function of x, such as f(u) = e^u where u is some function of x, the derivative is still e^u times the derivative of the exponent (u').
What is the derivative of e^(4x^3) using the chain rule?
-The derivative of e^(4x^3) is 12x^2 * e^(4x^3), which is obtained by multiplying e^(4x^3) by the derivative of the exponent 4x^3, which is 12x^2.
How is the product rule applied in the case of 3t * e^(3t^2 + 5t)?
-The derivative involves both the constant multiple rule and the chain rule. The derivative of 3t is 3, and the derivative of e^(3t^2 + 5t) is e^(3t^2 + 5t) times the derivative of the exponent (60 + 5t). The final answer is 3 * 60 + 5 * 3t, which simplifies to 180 + 15t.
What is the derivative of the quotient e^(3w) / (e^(3w) * 3)?
-Using the quotient rule, the derivative is (3 * e^(3w) - e^(3w) * 3w) / (e^(6w) * 9), which simplifies to (1 - 3w) / e^(3w).
How is the future value of an investment calculated with continuous compounding at an 8% annual rate?
-The future value S(T) of an investment with continuous compounding at an 8% annual rate is given by S(T) = 100 * e^(0.08T), where T is the time in years.
What is the rate of growth of money in the account after one year, according to the given script?
-The rate of growth of money in the account after one year is approximately $8.67, as found by evaluating the derivative of S(T) at T = 1.
What is the general formula for the derivative of a constant raised to the power of a variable, such as a^x?
-The derivative of a^x, where a is a constant, is a^x * ln(a), which is the constant times the natural logarithm of the base.
How does the derivative of an exponential function change when the base is not Euler's number?
-When the base is not Euler's number, the derivative of a^u, where u is a function of x, is a^u * ln(a) * u', which is the exponential function times the natural logarithm of the base and the derivative of the exponent.
What is the derivative of 4^x * ln(4)?
-The derivative of 4^x * ln(4) is simply 4^x * ln(4), as ln(4) is a constant factor that can be taken out of the derivative.
How is the derivative of the function a^(u(x)) calculated when a is a constant and u(x) is x^2 + x?
-The derivative is a^(x^2 + x) * ln(a) * (2x + 1), which applies the chain rule by taking the derivative of the exponent and multiplying by the constant ln(a).
Outlines
📈 Derivatives of Exponential Functions
This paragraph introduces the concept of derivatives for exponential functions, focusing on the natural exponential function with Euler's constant as the base. It explains that the derivative of the function e^x is the function itself, and demonstrates how to apply this to more complex functions involving exponents and the chain rule. Examples include taking the derivative of e^(4x^3) and a product involving e^(3t^2 + 5t). The paragraph also covers the quotient rule for derivatives and provides an application of exponential functions in the context of financial growth, specifically continuous compounding.
💹 Applications of Exponential Functions in Finance
This paragraph explores the application of exponential functions in financial contexts, particularly in calculating the future value of an investment with continuous compounding. It discusses how to find the rate at which money in an account grows by taking the derivative of the future value function s(T) = 100e^(0.08T). The derivative is calculated, and the growth rate at the end of one year and during the 11th year is determined. The paragraph also touches on exponential functions with bases other than e, showing how to find their derivatives when the base is a constant raised to the power of a variable, and when the exponent itself is a function of the variable.
Mindmap
Keywords
💡Derivatives
💡Exponential Functions
💡Euler's Constant
💡Tangent Line
💡Chain Rule
💡Power Rule
💡Product Rule
💡Quotient Rule
💡Continuous Compounding
💡Natural Logarithm
💡Marginal Growth
Highlights
The natural exponential function with Euler's constant as the base has a unique property where its derivative is the same as the function itself.
For a function f(u) = e^u, where u is a function of x, the derivative is e^u times the derivative of u, illustrating the chain rule.
Example given for the derivative of e^(4x^3), resulting in 12x^2 * e^(4x^3) using the power rule and chain rule.
Product rule applied to 3t * e^(3t^2 + 5t), showcasing a combination of constant multiplication, power rule, and chain rule.
Simplified expression for the derivative of the product rule example by factoring out e^(3t^2 + 5t) and reducing the expression.
Quotient rule demonstrated with the derivative of e^(3w)/3, resulting in (1 - 3w) / e^(3w) after simplification.
Application of exponential functions to financial growth, such as continuous compounding of an investment.
Future value of an investment calculated using the formula s(T) = 100 * e^(0.08T), where T is the time in years.
Derivative of the future value function s(T) used to find the rate of growth of the investment, resulting in 8e^(0.08) dollars per year.
Practical example: The investment grows by approximately $8.67 in the second year and $17.80 in the 11th year.
Derivative of an exponential function with a base other than e, such as a^x, results in a^x * ln(a) * derivative of x.
For a constant a raised to a function of x, the derivative involves the natural logarithm of the base a and the derivative of the function.
Example provided for a = 4 and u = x^2 + x, resulting in the derivative 4^(x^2 + x) * ln(4) * (2x + 1).
The importance of expressing rates of change in monetary terms, including cents for accuracy in financial calculations.
The transcript emphasizes the algebraic manipulation and simplification skills required to solve derivative problems.
The use of the chain rule in finding derivatives of composite exponential functions is a recurring theme throughout the transcript.
The transcript provides a comprehensive understanding of derivatives of exponential functions, both in general form and in practical applications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: