Simple Harmonic Motion - Springs in series vs parallel, and vertical springs
TLDRThis video script delves into the physics of simple harmonic motion, focusing on horizontal spring-mass systems. It explores the angular frequency and oscillation period for a single spring-mass system and compares it to systems with springs in parallel and series. The script also touches on the differences in vertical spring systems, highlighting the importance of understanding equilibrium and the role of spring constants in determining oscillation characteristics. The presentation aims to clarify the principles behind spring dynamics, providing a foundation for further exploration of mass-spring systems.
Takeaways
- 📚 The script discusses simple harmonic motion, focusing on horizontal spring systems with varying configurations.
- 🔍 It compares the angular frequency (Ω) and period of oscillation for different spring arrangements: single spring, springs in parallel, and springs in series.
- 📐 The first case examined is a single spring with mass M, characterized by spring constant K, and the displacement X from equilibrium is considered.
- ⚖️ Newton's second law is applied to derive the differential equation for the motion of the mass on the spring, leading to the equation ( m(d^2x)/(dt^2) = -kx ).
- 🌀 The solution to the differential equation is given by ( x(t) = a cos(Ω t + φ) ), where ( Ω = sqrt(k/m) ) is the angular frequency for the single spring case.
- 🔄 For springs in parallel, the effective spring constant is the sum of the individual spring constants, affecting the system's frequency of oscillation.
- 🔗 In the case of springs in series, the effective spring constant is found by the formula ( 1/K_{effective} = 1/K1 + 1/K2 ), which is different from the parallel case.
- 📉 The angular frequency for the series configuration is lower than for the parallel configuration, given the same spring constants.
- 📈 The script also touches on the differences between horizontal and vertical spring-mass systems, highlighting the importance of initial stretching in vertical systems.
- 🔍 The equilibrium position in a vertical spring system is influenced by the weight of the attached mass, which is a key difference from the horizontal system.
- 🚫 The script points out the limitation of the model when mass approaches zero, indicating a need for a more complex model that accounts for the mass of the spring itself in future discussions.
Q & A
What is the main focus of the script when discussing simple harmonic motion?
-The script focuses on analyzing the angular frequency (ω) and the period of oscillation for different horizontal spring-mass systems, including single spring, parallel springs, and series springs configurations.
What is the formula for the angular frequency of a simple spring-mass system?
-The angular frequency (ω) of a simple spring-mass system is given by the square root of the spring constant (k) divided by the mass (m), or ω = √(k/m).
How does the effective spring constant change when two springs are connected in parallel?
-When two springs with spring constants k1 and k2 are connected in parallel, the effective spring constant (k_effective) is the sum of the individual spring constants, k_effective = k1 + k2.
What is the effective spring constant when two springs are connected in series?
-For two springs in series with spring constants k1 and k2, the effective spring constant (k_effective) is calculated as k1 * k2 / (k1 + k2).
What is the difference between the horizontal spring-mass system and the vertical spring-mass system discussed in the script?
-The main difference is that in the vertical spring-mass system, there is an initial stretching of the spring (ΔX) due to the weight of the attached mass, which affects the equilibrium position and the calculation of the spring force.
How does the equilibrium position of a vertical spring-mass system differ from that of a horizontal spring-mass system?
-In a vertical spring-mass system, the equilibrium position includes an initial stretching (ΔX) due to the weight of the mass, whereas in a horizontal system, the equilibrium position is typically at the natural length of the spring with no initial stretching.
What happens to the angular frequency if the mass in a spring-mass system is set to zero?
-If the mass is set to zero, the formula for angular frequency would result in an undefined or infinite value, which is physically meaningless as it implies an infinite rate of oscillation without mass.
What is the relationship between the angular frequency and the period of oscillation?
-The period of oscillation (T) is related to the angular frequency (ω) by the formula T = 2π / ω. It represents the time taken for one complete cycle of oscillation.
Why is it necessary to consider the mass of the spring itself in more realistic models?
-Considering the mass of the spring itself is important because it can affect the dynamics of the system, especially at higher frequencies where the spring's own mass may cause it to vibrate, influencing the system's behavior.
What is the significance of the phase factor in the solution for simple harmonic motion?
-The phase factor in the solution for simple harmonic motion accounts for the initial conditions of the system, such as the starting position and velocity, and ensures the solution matches the actual motion at the beginning of the observation.
Outlines
🔍 Introduction to Simple Harmonic Motion with Springs
This paragraph introduces the topic of simple harmonic motion, focusing on horizontal spring systems. The speaker plans to solve three problems involving a single spring, springs in parallel, and springs in series, each attached to a block. The goal is to compare the angular frequency (ω) and period of oscillation across these configurations. The speaker also mentions the importance of understanding differences in vertical spring-mass systems, which will be briefly discussed later. A sketch of the three cases is presented, and the first case involves a single spring with spring constant K and mass M, stretched a distance X from equilibrium.
📚 Horizontal Spring Systems: Single Spring and Parallel Springs
The speaker delves into the dynamics of a single spring attached to a block and then discusses the scenario of two springs in parallel. For the parallel springs, the effective spring constant is calculated as the sum of the individual spring constants. The angular frequency for oscillation in both cases is derived using Hooke's law and Newton's second law, leading to the conclusion that the effective spring constant directly influences the frequency of oscillation. The summary of forces and the application of Newton's second law are explained in detail for both single and parallel spring setups.
🔧 Series Springs and Effective Spring Constant Calculation
This section explores the behavior of two springs in series with each other and how to calculate the effective spring constant for this configuration. The effective spring constant is found by taking the harmonic mean of the individual spring constants (1/K_effective = 1/K1 + 1/K2). The speaker applies a force to stretch the springs and uses the equilibrium condition to derive the relationship between the forces and displacements. The angular frequency for the series spring system is then found to be √(K_effective/m), highlighting the impact of the effective spring constant on the system's oscillation frequency.
📉 Comparing Angular Frequency and Period of Oscillation
The speaker compares the angular frequency and period of oscillation for the three different horizontal spring configurations: a single spring, springs in parallel, and springs in series. The effective spring constants for each case are used to calculate the angular frequencies, which are then related to the periods of oscillation. It is shown that the parallel configuration has the highest angular frequency, followed by the single spring, and then the series configuration. The summary includes a chart that visually represents the effective spring constants and the resulting frequencies for each case.
🌟 Vertical Spring Systems and Equilibrium Considerations
The discussion shifts to vertical spring systems, emphasizing the differences from horizontal systems due to gravity's influence. The speaker outlines three cases: a free spring, a spring with a mass attached in equilibrium, and a spring-mass system perturbed from equilibrium. The importance of the initial stretch (ΔX) in the equilibrium position is highlighted, and it is shown that this stretch is equal to the weight of the mass divided by the spring constant. The forces acting on the mass in the equilibrium and perturbed states are analyzed, leading to the conclusion that the equilibrium condition simplifies the force equation.
🔄 Angular Frequency for Vertical Spring Systems
The speaker concludes that the angular frequency for a vertical spring system with a mass attached is the same as for a horizontal system, which is √(K/m). However, it is noted that the equilibrium position for a vertical spring is not at its natural length due to the initial stretch caused by the weight of the mass. The paragraph ends with a teaser for the next discussion, which will address the assumption of massless springs and introduce the concept of a spring with mass, promising a more realistic analysis of spring systems.
Mindmap
Keywords
💡Simple Harmonic Motion
💡Angular Frequency (Omega)
💡Spring Constant (K)
💡Mass (M)
💡Horizontal Spring System
💡Parallel Springs
💡Series Springs
💡Frequency of Oscillation
💡Period of Oscillation
💡Freebody Diagram
💡Vertical Spring System
Highlights
Introduction to simple harmonic motion and horizontal spring systems.
Exploration of three different cases involving a single spring, springs in parallel, and springs in series.
Discussion on the angular frequency (Omega) and its importance in different spring-mass systems.
Calculation of the frequency and period of oscillation for various horizontal spring configurations.
Freebody diagram analysis for a block attached to a single spring.
Application of Newton's second law to derive the differential equation for simple harmonic motion.
Solution of the differential equation using a trial function for displacement.
Derivation of the angular frequency formula for a single spring-mass system.
Effective spring constant calculation for springs in parallel and its impact on angular frequency.
Effective spring constant for springs in series and its derivation from individual spring constants.
Comparison of angular frequencies for single, parallel, and series spring configurations.
Introduction to vertical spring-mass systems and their differences from horizontal systems.
Analysis of equilibrium position in a vertical spring system with a mass attached.
Application of Newton's second law to a vertical spring system and derivation of its differential equation.
Identification of the same angular frequency for vertical spring systems as in horizontal ones.
Discussion on the physical implications of mass on angular frequency in spring systems.
Teaser for the next session, which will consider the mass of the spring itself in the analysis.
Transcripts
Browse More Related Video

Simple Harmonic Motion - Complete Review of the Mass-Spring System
How To Solve Simple Harmonic Motion Problems In Physics
Simple Harmonic Motion, Mass Spring System - Amplitude, Frequency, Velocity - Physics Problems
AP Physics 1: Simple Harmonic Motion Review
AP Physics Workbook 6.E Equilibrium on an Incline
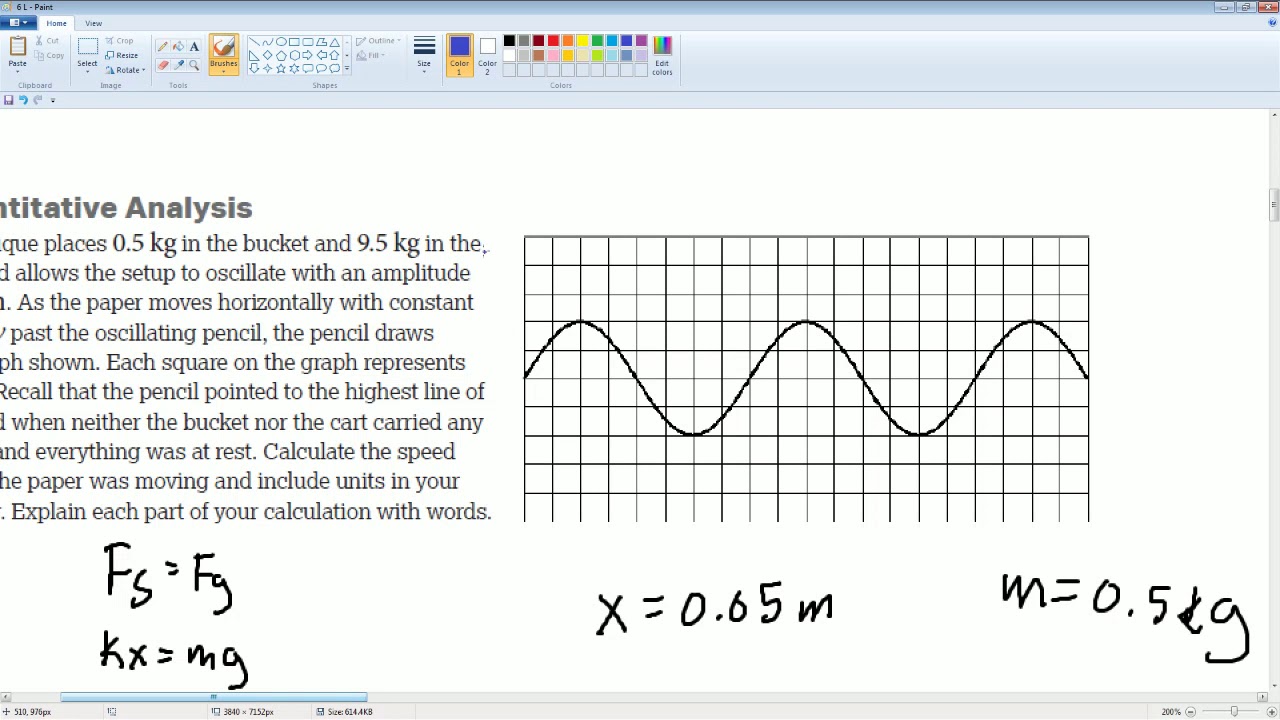
AP Physics Workbook 6.L Sine function of SHM
5.0 / 5 (0 votes)
Thanks for rating: