Simple Harmonic Motion, Mass Spring System - Amplitude, Frequency, Velocity - Physics Problems
TLDRThis script delves into the concept of periodic motion, particularly simple harmonic motion as seen in mass-spring systems and pendulums. It explains the restoring force, Hooke's Law, and the role of the spring constant. The script covers the calculation of forces, displacements, and the energy involved in oscillation. It further explores the effects of friction on damping, the significance of resonant frequency, and the mathematical functions that describe the motion of oscillators, including amplitude, frequency, period, and their interrelationships.
Takeaways
- 🔁 Periodic motion is a repetitive or oscillating movement, exemplified by simple harmonic motion such as a mass-spring system or a simple pendulum.
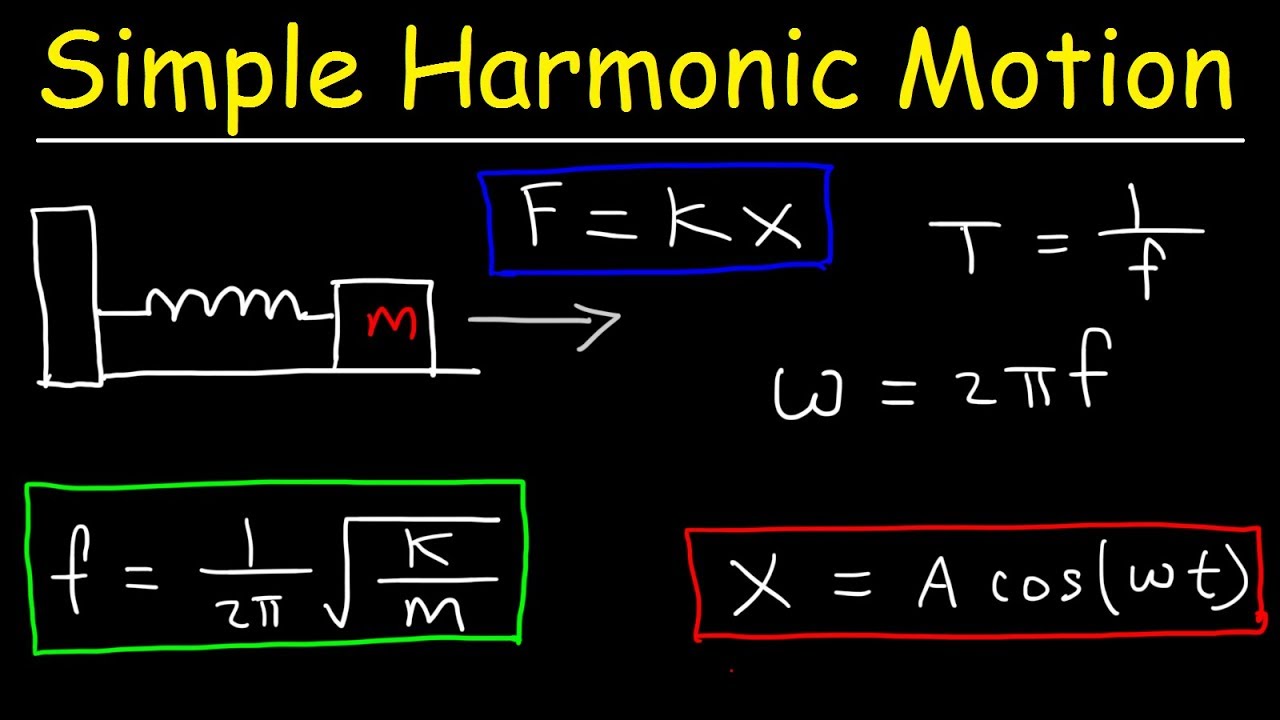
- 🔧 In a mass-spring system, the restoring force is the force that pushes the mass back towards its equilibrium position and is described by Hooke's law: F = -kx, where k is the spring constant and x is the displacement from equilibrium.
- ⚖️ Hooke's law incorporates a negative sign to indicate that the restoring force acts in the opposite direction of the displacement vector, aiming to return the system to its equilibrium state.
- 🔢 The spring constant (k) measures the stiffness of the spring and is expressed in newtons per meter, determining the force needed to stretch or compress the spring by a certain distance.
- 📏 Displacement (x) in Hooke's law is the distance the spring is stretched or compressed from its equilibrium position, crucial for calculating the restoring force.
- 📚 Practice problems in the script demonstrate how to calculate the force required to stretch a spring to a certain length and how to determine the distance a spring can be compressed given a specific force.
- 📉 The presence of friction in an oscillatory system will cause damping, reducing the amplitude of oscillations over time until the motion stops.
- 🔄 The energy of a mass-spring system oscillates between kinetic and potential forms; at the equilibrium position, kinetic energy is maximum, and potential energy is zero, while at full stretch or compression, the opposite is true.
- 🌀 The frequency and period of a spring-mass oscillator are inversely related; the period (T) is given by T = 2π√(m/k), and frequency (f) is the inverse of the period, f = 1/T.
- ⏫ An increase in mass or a decrease in the spring constant results in an increase in the period of oscillation, while an increase in the spring constant leads to a decrease in the period.
- 📐 The resonant frequency occurs when an external force is applied at the natural frequency of the oscillator, leading to maximum amplitude and potential energy transfer to the system.
Q & A
What is periodic motion?
-Periodic motion is a type of motion that repeats itself or oscillates back and forth. Examples include the motion of a mass-spring system and a simple pendulum.
What is simple harmonic motion?
-Simple harmonic motion is a type of periodic motion where an object moves back and forth over the same path within a stable system, such as a mass attached to a spring.
What causes the restoring force in a mass-spring system?
-The restoring force in a mass-spring system is caused by the spring's tendency to return to its equilibrium position after being stretched or compressed.
What is Hooke's Law and how is it expressed mathematically?
-Hooke's Law states that the restoring force in a spring is directly proportional to the displacement from the equilibrium position and is equal to negative one times the spring constant (k) times the displacement (x), expressed as F_r = -kx.
What is the spring constant and what are its units?
-The spring constant, denoted by k, is a measure of the stiffness of a spring. Its units are newtons per meter (N/m).
Why is there a negative sign associated with the restoring force in Hooke's Law?
-The negative sign in Hooke's Law indicates that the restoring force always acts in the opposite direction of the displacement from the equilibrium position.
How does the force required to stretch or compress a spring relate to the spring constant and the distance of displacement?
-The force required to stretch or compress a spring is directly proportional to the spring constant and the distance of displacement from the equilibrium position, as given by the equation F = kx.
What is the relationship between the force applied to a spring and the distance it is stretched or compressed?
-The force applied to a spring is proportional to the distance it is stretched or compressed. If the force is doubled, the distance will also double, assuming the spring constant remains the same.
What is the potential energy stored in a spring when it is stretched or compressed, and how is it calculated?
-The potential energy stored in a spring is given by the formula U = (1/2)kx^2, where k is the spring constant and x is the displacement from the equilibrium position.
What happens to the amplitude of oscillation in a damped harmonic motion?
-In damped harmonic motion, the amplitude of oscillation decreases over time due to the presence of friction or other resistive forces that dissipate the system's energy.
What is the resonant frequency and why is it significant?
-The resonant frequency is the frequency at which the amplitude of an oscillator's motion is at its maximum because the applied frequency matches the natural frequency of the system. It is significant because it is the most effective frequency for transferring energy to the oscillator.
What are the different types of damping and how do they affect the motion of an oscillator?
-There are three types of damping: underdamped, overdamped, and critically damped. Underdamped systems oscillate multiple times before coming to rest. Overdamped systems do not oscillate and take a long time to reach rest. Critically damped systems reach rest as quickly as possible without oscillating.
How can the frequency and period of a spring-mass oscillator be determined?
-The frequency (f) of a spring-mass oscillator can be determined using the formula f = 1 / (2π) * √(k/m), where k is the spring constant and m is the mass. The period (T) is the reciprocal of the frequency, T = 1/f.
What is the relationship between the spring constant and the period of oscillation for a spring-mass system?
-The period of oscillation for a spring-mass system is inversely related to the square root of the spring constant. If the spring constant is increased, the period decreases, and vice versa.
How does the mass of an object attached to a spring affect the period of its oscillation?
-The mass of an object attached to a spring affects the period of its oscillation inversely. If the mass is increased, the period increases because the system has more inertia and takes longer to complete a cycle.
Outlines
🔁 Introduction to Periodic Motion and Simple Harmonic Motion
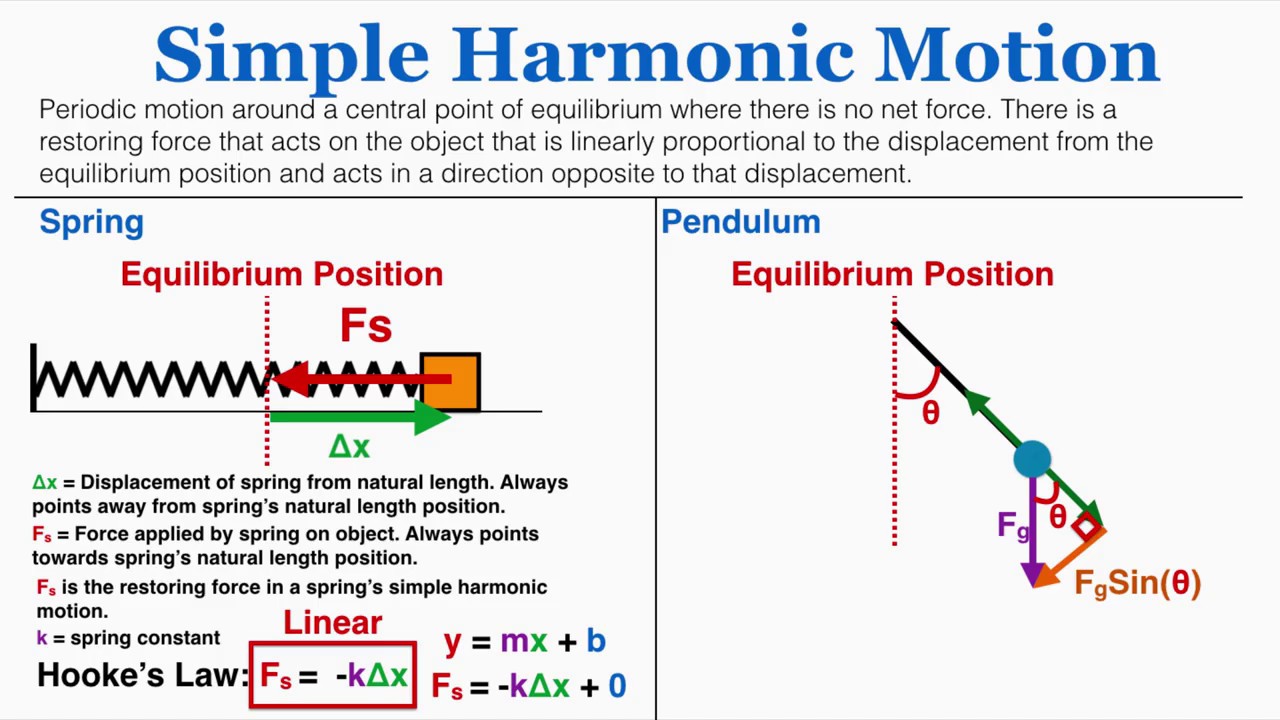
The paragraph introduces the concept of periodic motion, which is a type of motion that repeats itself, such as oscillating back and forth. Simple harmonic motion (SHM) is highlighted as a specific type of periodic motion exemplified by a mass-spring system and a simple pendulum. The mass-spring system is used to explain the concept of equilibrium position and the restoring force, which pulls the mass back towards this position. Hooke's Law is introduced to quantify the restoring force as being proportional to the displacement from the equilibrium position, with the spring constant (k) being a measure of the stiffness of the spring.
🔧 Practice Problems on Spring Force and Displacement
This section focuses on practical applications of Hooke's Law through a series of problems. It demonstrates how to calculate the force required to stretch a spring by a certain distance and vice versa, how much the spring can be compressed with a given force, and the relationship between force, displacement, and the spring constant. The concept of the negative sign in Hooke's Law is clarified, indicating the direction of the restoring force in opposition to the displacement.
🔄 Work, Energy, and the Spring-Mass System
The discussion continues with the calculation of work done to stretch a spring and the potential energy stored in it. The work-energy principle is applied to find the work required to stretch a spring to a certain displacement, and the concept of elastic potential energy is introduced as the energy stored in a spring during deformation. The relationship between the spring constant, displacement, and potential energy is explored, along with the behavior of a mass-spring system when released from rest.
📉 Impact of Friction on Oscillation and Displacement Analysis
The role of friction in a mass-spring system is examined, explaining how friction opposes motion and leads to dampened oscillations. The effects of friction on the amplitude of oscillation are discussed, and the impact of friction on the system's energy is described. The paragraph also explores the restoring force at various displacements and how the force influences the motion of the oscillator, including the transition points where velocity and acceleration are at their maximum or minimum.
🚀 Energy Conservation in Oscillatory Motion
This section delves into the conservation of mechanical energy in a mass-spring system, detailing the interplay between kinetic and potential energy during oscillation. The conditions for maximum and minimum kinetic and potential energy are explained, along with the calculation of maximum velocity and acceleration. The importance of amplitude in determining the system's total mechanical energy is emphasized, and equations relating displacement to velocity and acceleration are provided.
📚 Mathematical Representation of SHM and Its Characteristics
The paragraph introduces the mathematical representation of simple harmonic motion, including the equations for displacement, velocity, and acceleration as functions of time and amplitude. The relationships between these quantities are derived, and the significance of the spring constant and mass in determining the system's behavior is discussed. The importance of understanding the direction of velocity and the role of maximum velocity in SHM is highlighted.
⏱ Frequency and Period of a Spring-Mass Oscillator
The concepts of frequency and period in the context of a spring-mass oscillator are explained, along with their relationship to the spring constant and mass. The paragraph describes how to calculate the time it takes to complete one cycle and the number of cycles per second. The inverse relationship between frequency and period is established, and the impact of changes in displacement on the system's total energy, maximum velocity, and maximum acceleration is explored.
🔄 Calculation of Spring Constant and Oscillation Characteristics
This section involves the calculation of the spring constant using force and displacement data, followed by the determination of maximum velocity, maximum acceleration, and the velocity at a specific displacement from the equilibrium position. The process of calculating the restoring force and acceleration at a given displacement is detailed, emphasizing the importance of these quantities in understanding the behavior of a spring-mass system.
📐 Comparing Circular Motion with Simple Harmonic Motion
The paragraph draws a comparison between circular motion and simple harmonic motion, particularly focusing on the appearance of circular motion when viewed from the side and its similarity to the oscillation of a spring. The relationship between the speed of an object in circular motion and its period is discussed, along with the connection between the radius of the circle and the amplitude of SHM.
⚖️ Effect of Mass and Spring Constant on Oscillation Period
The relationship between the mass of the object, the spring constant, and the period of oscillation is explored, with the period expressed as a function of these variables. The effects of increasing or decreasing the mass and spring constant on the period are examined, and the conceptual understanding of why a stiffer spring or a heavier mass influences the period is explained.
🔢 Calculation of Frequency and Period for Given Conditions
This section provides examples of calculating the frequency and period of oscillation for a mass-spring system given specific conditions. The process involves determining the spring constant from the applied force and displacement, and then using it to find the frequency and period. The calculations are demonstrated with numerical examples, showing how to arrive at the frequency in hertz and the period in seconds.
🕊️ Insect in a Spider Web: Finding Spring Constant and Frequency
The paragraph presents a problem involving an insect caught in a spider web, where the mass of the insect and its frequency of oscillation are known, and the spring constant needs to be determined. The process involves using the frequency to find the spring constant and then using the new mass to find the new frequency. The calculations are demonstrated step by step, showing the application of the formulas for frequency and spring constant.
🔄 Frequency Comparison of Spring Systems with Different Constants
This section compares the frequencies of oscillation for a block attached to springs with different force constants. The relationship between the spring constant and frequency is used to determine how changes in the spring constant affect the frequency of oscillation. The calculations demonstrate the increase in frequency with an increase in spring constant and vice versa.
📏 Total Distance Traveled by a Block in Simple Harmonic Motion
The paragraph calculates the total distance traveled by a block undergoing simple harmonic motion over a certain number of periods. By understanding the relationship between the amplitude, period, and the distance traveled in one cycle, the total distance for multiple periods is determined. The calculation shows the distance covered by the block as it oscillates back and forth.
📈 Graphing and Understanding SHM Functions
This section explains how to graph and interpret the sinusoidal functions that describe the motion of a mass-spring system. The position, velocity, and acceleration functions of time are derived from the basic principles of SHM, and their graphical representations are discussed. The role of calculus in finding the velocity and acceleration functions from the position function is highlighted.
📚 Energy and Dynamics in a Mass-Spring System
The paragraph delves into the energy and dynamics of a mass-spring system, discussing the calculation of total energy, potential energy, and kinetic energy. The conditions for maximum and minimum energies are explained, and the process of finding the energies at various displacements is demonstrated. The importance of understanding the conservation of mechanical energy in SHM is emphasized.
🔁 Damped Harmonic Motion and Its Characteristics
This section introduces damped harmonic motion, which occurs when friction or other resistive forces are present in a vibrating system. The effects of damping on the amplitude of oscillation are discussed, and the three types of damping—overdamping, underdamping, and critical damping—are defined and compared. The practical applications of damping in devices such as car shock absorbers are also mentioned.
📉 Resonance and Its Effect on Oscillator Amplitude
The concept of resonance is explored, explaining how the application of a force at the natural frequency of an oscillator can significantly increase its amplitude. The phenomenon is illustrated with the example of a child on a swing, and the importance of applying force at the resonant frequency for maximum effect is discussed.
Mindmap
Keywords
💡Periodic Motion
💡Simple Harmonic Motion (SHM)
💡Restoring Force
💡Hooke's Law
💡Spring Constant (k)
💡Equilibrium Position
💡Displacement (x)
💡Damping
💡Frequency and Period
💡Resonant Frequency
💡Potential and Kinetic Energy
Highlights
Periodic motion is defined as motion that repeats itself or oscillates back and forth, exemplified by simple harmonic motion in mass-spring systems and pendulums.
In a mass-spring system, the restoring force is the force that pushes the mass back towards its equilibrium position and is described by Hooke's law (F = -kx), where k is the spring constant and x is the displacement from equilibrium.
Hooke's law includes a negative sign indicating that the restoring force is always opposite to the direction of displacement, essential for the oscillation to occur.
The spring constant (k) measures the stiffness of the spring, with higher values indicating a stiffer spring that requires more force to stretch or compress.
Practice problems illustrate the calculation of force required to stretch or compress a spring, emphasizing the relationship between force, spring constant, and displacement.
The concept of potential energy in a spring is introduced, calculated as (1/2)kx^2, representing the work done to stretch or compress the spring.
Mechanical energy conservation in a mass-spring system is discussed, highlighting that the sum of kinetic and potential energy remains constant if no external forces act.
The maximum velocity and acceleration of a mass in simple harmonic motion are derived, showing how they relate to the spring constant, mass, and amplitude.
The velocity of a mass as a function of its displacement from equilibrium is provided, incorporating the maximum velocity and the current displacement.
The frequency and period of a spring-mass oscillator are explained, with formulas relating them to the spring constant and mass.
Damped harmonic motion is introduced, describing how friction or other resistive forces reduce the amplitude of oscillation over time.
Different types of damping (over-damped, under-damped, and critically damped) are described, each affecting the oscillator's behavior differently.
Resonant frequency is discussed as the frequency at which an oscillator's amplitude is maximized when the applied frequency matches the natural frequency of the system.
The importance of resonant frequency in practical applications, such as minimizing bounce in car shock absorbers or maximizing the amplitude of a swing, is highlighted.
The role of friction in dampening oscillations is further elaborated, with examples of how it affects the oscillator's energy and amplitude.
A detailed walkthrough of solving practice problems related to spring constants, amplitudes, and energy calculations in oscillatory systems is provided.
Transcripts
Browse More Related Video

Simple Harmonic Motion - Complete Review of the Mass-Spring System
How To Solve Simple Harmonic Motion Problems In Physics
AP Physics Workbook 6.L Sine function of SHM

01 - Oscillations And Simple Harmonic Motion, Part 1 (Physics Tutor)

AP Physics 1 review of Waves and Harmonic motion | Physics | Khan Academy
Simple Harmonic Motion - IB Physics
5.0 / 5 (0 votes)
Thanks for rating: