AP Physics Workbook 6.L Sine function of SHM

Mr.S ClassRoom
15 Apr 202011:54
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses Unit 6 on Simple Harmonic Motion from an AP Physics workbook, focusing on the effects of mass and spring constant on the period and amplitude of oscillation. It explains how altering the mass of a system can change the period and amplitude, using the formula for period involving mass and the spring constant. The video also delves into the concept of damping in harmonic motion due to friction, resulting in a decrease in amplitude over time. Calculations are provided to determine the spring constant and the velocity of the oscillating mass, emphasizing the understanding of physical principles in a harmonic motion scenario.

Takeaways
  • πŸ“š The script discusses Unit 6 on Simple Harmonic Motion, focusing on the sine function related to it.
  • πŸ”§ Part A involves adjusting the mass m of an object to change the period of a simple harmonic motion.
  • πŸ’‘ The top period (T) of simple harmonic motion is given by the formula T = 2Ο€βˆš(mK), where m is the mass and K is the spring constant.
  • πŸ”„ To halve the period, the mass should be halved due to the linear relationship between mass and period.
  • πŸ“ˆ Doubling the period requires increasing the mass by a factor of 4, as the period is proportional to the square root of the mass.
  • 🎲 The scenario involves a bucket and a cart, where the mass on the cart affects the period of the pencil's oscillation, not the bucket.
  • πŸ“Œ Newton's second law is applied to find the spring constant (K) by setting up the equation KX = mg.
  • πŸš€ The velocity (V) of the object in simple harmonic motion is calculated using the formula V = 2Ο€R/T, where R is the amplitude.
  • πŸ“Š The graph of the simple harmonic motion shows a sine wave, with the amplitude representing the displacement of the object.
  • πŸ”Œ Damping is introduced in Part C, explaining that friction between the pencil and paper affects the vertical motion of the bucket, leading to a decrease in the oscillation amplitude over time.
  • 🌑️ The energy lost due to friction is dissipated as thermal energy, causing the amplitude of the oscillation to decrease, which is graphically represented as a reduction in the graph's peak over time.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is simple harmonic motion, specifically focusing on how changes in mass and spring constant affect the period and amplitude of oscillation.

  • How does the mass of the bucket affect the period of the pencil's oscillation?

    -The period of the pencil's oscillation is affected by the mass of the bucket because the period is determined by the formula T = 2Ο€βˆš(m/k), where m is the mass and k is the spring constant. To double the period, the mass on the cart (not the bucket) must be increased by a factor of 4, since the square root of 4 is equal to 2.

  • What is the relationship between the spring force and the gravitational force acting on the pencil?

    -The spring force and the gravitational force acting on the pencil are in linear relationship, as represented by the equation F_spring = -kx and F_gravity = -mg, respectively. The negative sign indicates that these forces act in opposite directions.

  • How does the weight of the bucket influence the pencil's position on the page?

    -The weight of the bucket drags the pencil downward on the page. To position the pencil in the middle of the page, the mass of the bucket needs to be reduced by half, due to the linear relationship between the forces acting on the pencil.

  • What is the calculated spring constant (k) based on the given data?

    -The calculated spring constant (k) is 100 N/m, derived from the equation k = mg/x, where m is the mass (0.5 kg), g is the acceleration due to gravity (approximately 10 m/s^2), and x is the displacement (0.05 m).

  • What is the period of the oscillation calculated to be?

    -The period of the oscillation is calculated to be 2 seconds, using the formula T = 2Ο€βˆš(m/k) with m being 0.01 kg (mass of the cart without the bucket) and k being 100 N/m.

  • How is the velocity of the cart determined?

    -The velocity of the cart is determined by considering the total distance traveled during one complete cycle of oscillation divided by the period of the oscillation. The total distance is estimated to be 8 cm (or 0.08 m) over a period of 2 seconds, resulting in a velocity of 0.04 m/s.

  • What happens to the amplitude of the oscillation due to friction between the pencil and the paper?

    -Due to friction between the pencil and the paper, the amplitude of the oscillation decreases over time. This is because the energy from the oscillating system is dissipated as thermal energy, leading to a reduction in the amplitude of the oscillation.

  • How does the damping of harmonic motion manifest on a graph?

    -On a graph, damping of harmonic motion is represented by a decrease in the amplitude of the oscillation over time. The graph would show the amplitude getting smaller with each successive cycle until the motion eventually stops.

  • What is the significance of the linear relationship between the spring force and the gravitational force?

    -The linear relationship between the spring force and the gravitational force is significant because it allows for the application of Hooke's Law and Newton's Second Law of Motion. It means that the forces are directly proportional to their respective quantities (spring displacement and gravitational weight), which is essential for calculating the system's behavior.

  • Why is it important to consider the effects of external forces in simple harmonic motion?

    -Considering the effects of external forces is important because it provides a more realistic model of physical systems. In nature, perfect simple harmonic motion is rare due to the presence of external forces like friction and air resistance, which cause damping and affect the system's energy conservation and oscillation characteristics.

Outlines
00:00
πŸ“š Simple Harmonic Motion and Mass Manipulation

This paragraph introduces the concept of simple harmonic motion and discusses a scenario where Dominick manipulates the mass of a system to achieve specific outcomes. The key focus is on understanding the relationship between mass, spring constant, and the period of oscillation. The hint provided emphasizes the formula for the period of a simple harmonic oscillator, which is given by T = 2Ο€βˆš(m/k). The scenario involves adjusting the mass of a bucket attached to a cart to change the amplitude of the pencil's movement on the paper. It is explained that reducing the mass of the bucket by half would result in the pencil reaching the middle of the page. Additionally, the paragraph explores the idea of increasing the period of oscillation by increasing the mass on the cart, as the period is dependent on the mass and spring constant. The mathematical reasoning behind these adjustments is explained, highlighting the linear relationship between the forces acting on the pencil (spring force and gravitational force) and the mass.

05:03
πŸ“ˆ Calculating Velocity and Understanding Damped Oscillation

The second paragraph delves into the calculation of velocity within the context of simple harmonic motion and introduces the concept of damped oscillation. The speaker first calculates the period of the oscillation using the previously derived spring constant and mass. The period is found to be two seconds using the formula T = 2Ο€βˆš(m/k). Following this, the speaker calculates the velocity by considering the total distance traveled during one complete cycle and the period of oscillation. The velocity is determined to be 0.04 meters per second after converting the units from centimeters to meters. The paragraph concludes with a discussion on damped harmonic motion, explaining that friction between the pencil and paper would convert the system's energy into thermal energy, leading to a decrease in the amplitude of oscillation over time. This results in a graphical representation where the amplitude of the oscillation graph decreases, demonstrating the effect of damping on the system's energy.

10:08
πŸ”„ Damping of Harmonic Motion and Energy Dissipation

The final paragraph focuses on the energy aspects of damped harmonic motion, emphasizing the energy transformations that occur when friction is present. It explains that in an oscillating system with friction, the mechanical energy would gradually dissipate as thermal energy, causing the amplitude of oscillation to decrease. The speaker provides two answers based on the notes, highlighting the impact of friction on the system's velocity and graphical representation. The explanation clarifies that the cart's speed decreases due to energy loss as heat, leading to smaller amplitudes over time. The graphical representation of damped harmonic motion is depicted as a gradual decrease in amplitude, illustrating the fundamental concept that harmonic motions are rarely perfect in nature due to the presence of external forces and energy losses.

Mindmap
Keywords
πŸ’‘Simple Harmonic Motion
Simple Harmonic Motion (SHM) is a type of periodic motion where an object oscillates back and forth around an equilibrium position. In the context of the video, SHM is exemplified by the movement of a mass attached to a spring. The motion is characterized by its periodic nature and can be described by a sine function. The video discusses how changes in mass and spring constant affect the period and amplitude of the oscillation.
πŸ’‘Period
The period of an oscillation is the time it takes for one complete cycle of the motion to occur. In the context of the video, the period is a key factor in understanding how the mass and spring constant influence the oscillation of the system. The formula for the period of a simple harmonic motion is given by T = 2Ο€βˆš(mass/spring constant), which shows the direct relationship between the mass and the period.
πŸ’‘Mass
In the context of physics and the video, mass refers to the amount of matter in an object, which determines its inertia and the gravitational force it experiences. The video discusses how altering the mass of the bucket affects the period and amplitude of the simple harmonic motion. By reducing the bucket's mass, the period can be adjusted, and by increasing the mass on the cart, the period can be lengthened.
πŸ’‘Spring Constant
The spring constant, denoted by K, is a measure of the stiffness of a spring. It describes the amount of force needed to extend or compress the spring by a certain distance. In the video, the spring constant is a crucial factor in the equations governing the simple harmonic motion, and it is mentioned that it cannot be changed in the given scenario.
πŸ’‘Displacement
Displacement in physics refers to the change in position of an object. In the context of the video, displacement is used to describe the movement of the mass (bucket) from its equilibrium position as it oscillates. The video uses the displacement to calculate the spring constant and to understand the behavior of the oscillating system.
πŸ’‘Velocity
Velocity is a vector quantity that describes the rate of change of an object's position with respect to time, taking into account both magnitude and direction. In the context of the video, velocity is used to describe the speed of the cart (mass on the cart) as it moves through its simple harmonic motion. The video provides a method to calculate the velocity based on the period and the total distance traveled during one complete cycle of the motion.
πŸ’‘Force
In physics, force is any action that causes an object to accelerate or change its motion. In the video, two forces are at play in the simple harmonic motion scenario: the spring force (restoring force) and the gravitational force. The spring force is represented by KX, where K is the spring constant and X is the displacement, while the gravitational force is represented by mg, where m is the mass and g is the acceleration due to gravity.
πŸ’‘Damping
Damping refers to the reduction of amplitude in oscillations due to the presence of resistive forces, such as friction or air resistance, which cause energy to be dissipated in the form of heat or sound. In the context of the video, damping is discussed in relation to the effect of friction between the pencil and the paper on the oscillation of the bucket.
πŸ’‘Amplitude
Amplitude in the context of oscillations is the maximum displacement of the oscillating object from its equilibrium position. It represents the extent of the motion and is a measure of the energy in the system. The video discusses how changes in amplitude occur due to damping forces like friction.
πŸ’‘Equilibrium Position
The equilibrium position is the position where the net force acting on an object is zero, and the object is at rest or in a state of balanced forces. In the video, the equilibrium position is the central point around which the mass oscillates in simple harmonic motion. Any deviation from this position results in the restoring force of the spring bringing the mass back towards equilibrium.
Highlights

Dominick's experiment involves adjusting the mass on a cart in simple harmonic motion to achieve specific outcomes.

The period of simple harmonic motion is related to the mass and spring constant, with the formula T = 2Ο€βˆš(m/k).

To double the period of the pencil's oscillation, the mass on the cart should be increased by a factor of 4.

The weight of the bucket affects the pencil's position on the page, with a halved bucket mass resulting in the pencil's position being raised.

The spring constant (k) can be calculated using the formula k = mg, where m is the mass and g is the acceleration due to gravity.

The velocity of an object in simple harmonic motion can be determined using the formula v = 2Ο€r/T, where r is the amplitude.

The actual velocity calculation involves converting the total distance traveled during one complete cycle over the period.

Friction between the pencil and paper introduces damping to the system, affecting the vertical motion of the bucket.

Damping in harmonic motion results in the dissipation of energy as thermal energy, leading to decreasing amplitude over time.

The effect of damping on the graph of harmonic motion would be a gradual decrease in amplitude with each successive cycle.

Simple harmonic motion is rarely found in nature due to the presence of external forces and damping effects.

The scenario involves understanding how mass affects the period and amplitude of simple harmonic motion.

The concept of linear relationships is discussed in the context of forces acting on the pencil, such as spring force and gravitational force.

The importance of considering the forces acting on the system, such as KX + mg, is emphasized for solving problems.

The method for calculating the velocity in the context of circular motion is compared to that of simple harmonic motion.

The impact of adding mass to the cart is discussed in terms of how it affects the period of oscillation.

Transcripts

Browse More Related Video

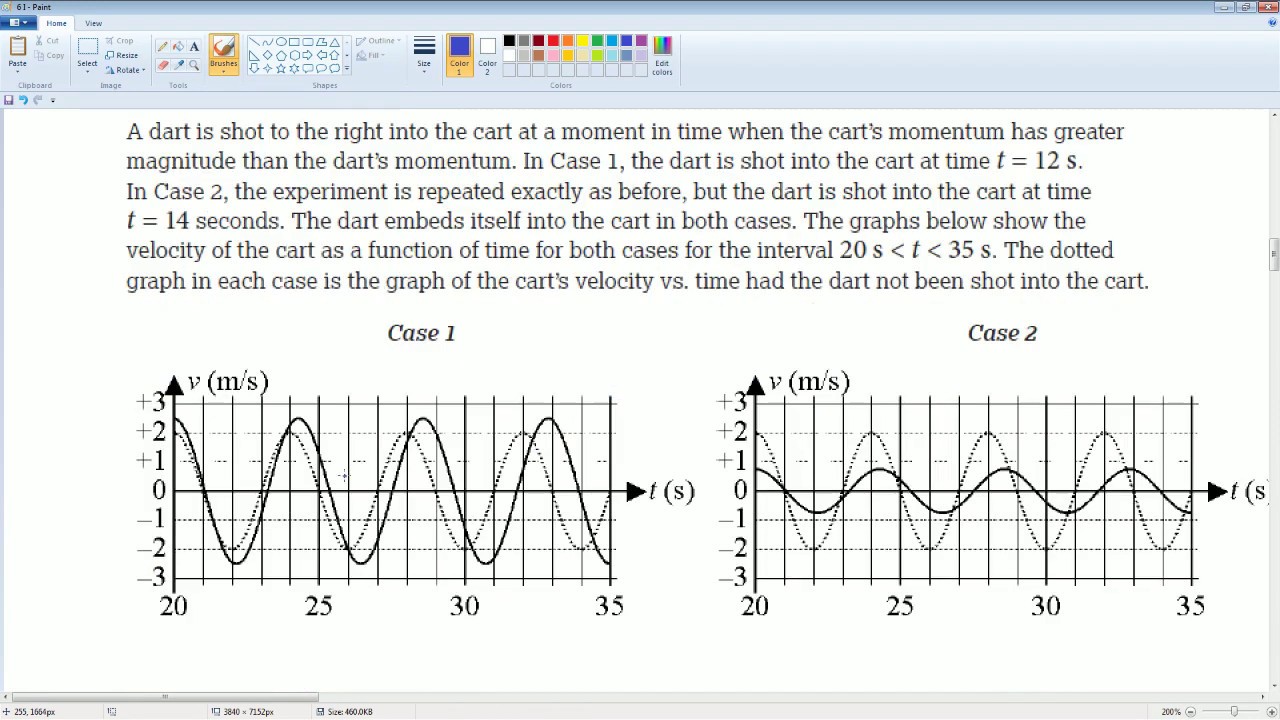
AP Physics Workbook 6.I Changing Mass and Period of a Mass Spring SYstem

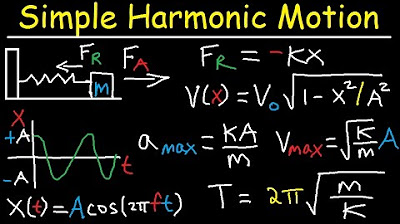
Simple Harmonic Motion, Mass Spring System - Amplitude, Frequency, Velocity - Physics Problems

Simple Harmonic Motion - Complete Review of the Mass-Spring System

2021 Live Review 6 | AP Physics 1 | Understanding Simple Harmonic Motion

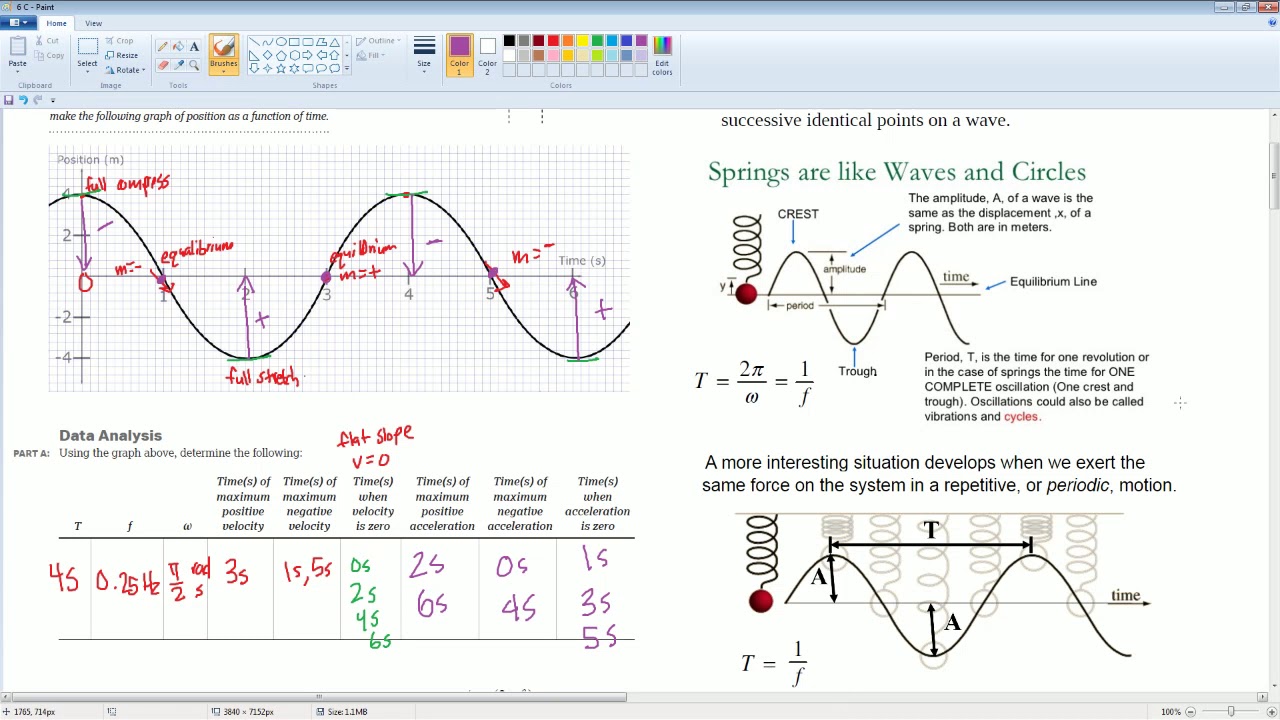
AP Physics Workbook 6.C Equations of Motion for Simple Harmonic Motion

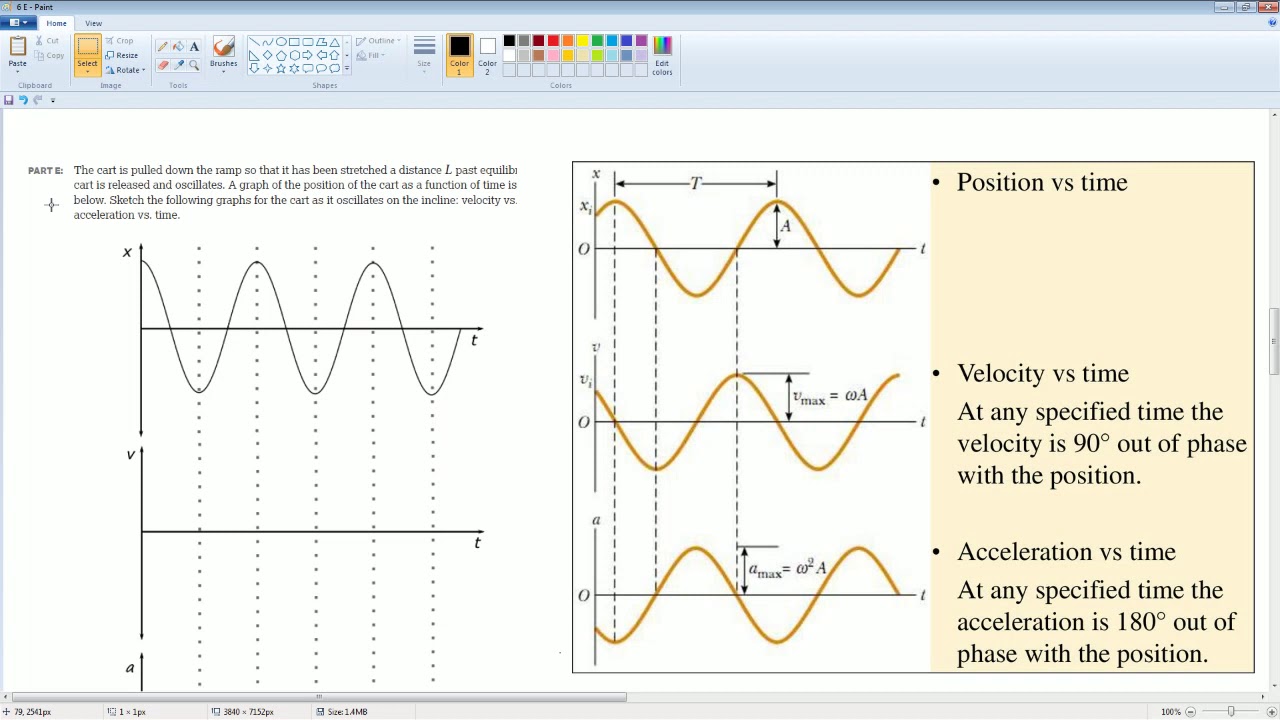
AP Physics Workbook 6.E Equilibrium on an Incline

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsConceptsHarmonicMotionSpringConstantMassAdjustmentDampingEffectsOscillationAmplitudeNewtonsLawsWorkedExamplesEducationalContentAPPhysics