AP Calculus AB: Lesson 7.5: Shell Method

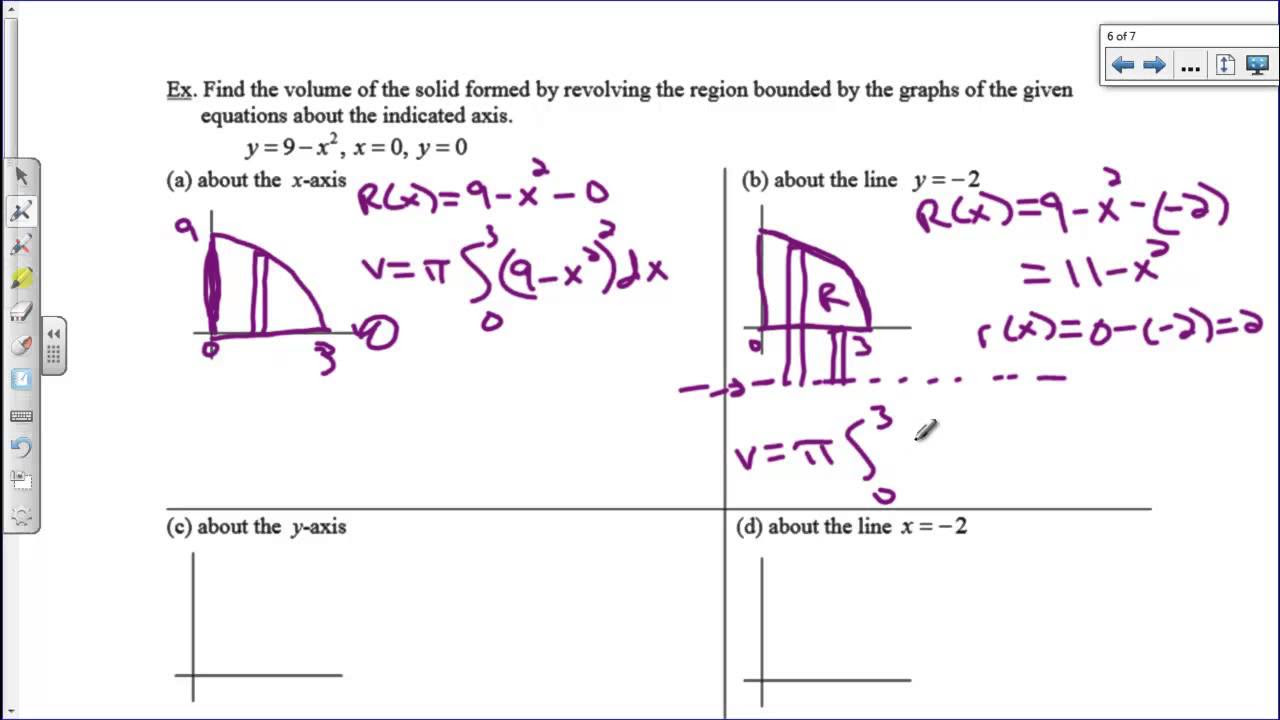
This paragraph introduces a new mathematical technique known as the Shell Method for calculating the volume of a solid of revolution, following a review of the Washer Method. The Washer Method involves using two separate disk methods and subtracting the results to account for the empty space within the solid. The paragraph explains the basic setup for the Washer Method, which includes multiplying PI by the integral from a to b of the outer radius squared minus the inner radius squared, times dx. The process involves finding the volume of the larger disc and subtracting the volume of the smaller disc, which represents the empty space. The paragraph also emphasizes the importance of drawing reference rectangles and understanding the interval for the integral when setting up the problem.

The second paragraph delves deeper into the application of the Washer Method by providing a step-by-step guide on how to find the point of intersection between two functions, f(x) and g(x), using a graphing calculator. It explains the process of setting up the integral for the volume of the solid formed by rotating the region between these two functions around the x-axis. The paragraph illustrates how to calculate the outer and inner radii for the Washer Method and how to perform the integration using a calculator. It concludes with a brief mention of considering alternative methods for more complex problems where the Washer Method might not be the best choice.

This paragraph discusses the limitations of using the Washer Method for certain functions, particularly when the function does not pass the horizontal line test, indicating that x is not a function of y. The speaker explains that in such cases, the Washer Method becomes impractical because it requires solving the equation for x, which can be complex. The paragraph uses the example of the function y = sin(x) and explains why it's difficult to apply the Washer Method in this scenario. It also highlights the importance of recognizing when a horizontal slice would not result in a washer shape, suggesting that the Shell Method might be more appropriate for such cases.

The speaker transitions from discussing the limitations of the Washer Method to introducing the Shell Method with a demonstrative example. They explain how to visualize and calculate the volume of a solid formed by rotating a region around the y-axis using horizontal slices, resulting in cylindrical shells. The paragraph outlines the process of finding the volume of a single shell and then summing these volumes using an integral. It emphasizes the lateral surface area of the cylinder and its relation to the radius and height, which are derived from the function and the axis of rotation.

In this paragraph, the speaker provides a detailed setup for using the Shell Method with the function y = sin(x) rotated around the y-axis. They explain how to determine the interval for the integral and how to rewrite the function in terms of x to avoid using multivariable calculus. The paragraph includes a step-by-step guide on setting up the integral, performing the integration on a calculator, and interpreting the result to find the volume of the solid. It also emphasizes the importance of drawing a well-labeled reference rectangle and a cylinder to visualize the problem.

The paragraph presents a comparison between the Shell Method and the Washer Method for finding the volume of a solid formed by revolving a region bounded by two functions around the y-axis. It discusses the difficulties associated with the Washer Method, such as the challenge of separating the graph into distinct parts and solving the equation for x. The speaker advises using the Shell Method for this particular problem and outlines the steps for setting up the integral, including determining the radius and height of the cylindrical shells.

This paragraph demonstrates the application of the Shell Method to a complex function, y = 2x^2 - x^3, rotated around the y-axis. The speaker explains the process of identifying the interval for the integral and setting up the integral with the correct expressions for the radius and height of the cylindrical shells. They also discuss the importance of drawing a reference rectangle and a cylinder to visualize the problem and to ensure the correct setup for the integral.

The paragraph discusses the use of the Shell Method for a region rotated around a vertical line, x = -1, using the function y = sqrt(x). It explains how to determine the interval for the integral and how to calculate the radius of the cylindrical shells, which is the horizontal distance from the axis of rotation to the curve. The speaker also provides a step-by-step guide on setting up the integral and performing the calculation to find the volume of the solid.

This paragraph explores the use of both the Shell Method and the Washer Method for finding the volume of a solid formed by revolving a region around the line x = 2. The speaker explains why the Washer Method would be difficult to apply due to the complexity of solving the equation for x and suggests using the Shell Method instead. They provide a detailed setup for the Shell Method, including determining the radius and height of the cylindrical shells and setting up the integral.

The paragraph presents a comparison of the Shell Method and the Washer Method for a region between two functions, y = x and y = x^2, rotated around the y-axis. The speaker demonstrates the setup for both methods, emphasizing the importance of understanding the geometry of the problem and the functions involved. They show that both methods, when applied correctly, yield the same result for the volume of the solid.

This paragraph discusses the application of the Shell Method for a region rotated around a horizontal axis, specifically the x-axis. The speaker explains how to set up the integral for the volume of the solid formed by the region under the curve y = sqrt(x) from x = 0 to x = 1. They provide a detailed explanation of determining the radius and height of the cylindrical shells and how to rewrite the expressions in terms of the variable of integration.

The final paragraph presents a comparison between the Shell Method and the Washer Method for finding the volume of a solid formed by revolving a region between two curves, x = y^3 and y = x, around the line y = -1. The speaker outlines the setup for both methods, including determining the radius and height for the cylindrical shells in the Shell Method and calculating the outer and inner radii for the Washer Method. They emphasize the importance of converting all expressions into terms of the variable of integration and highlight that both methods should yield the same result when applied correctly.