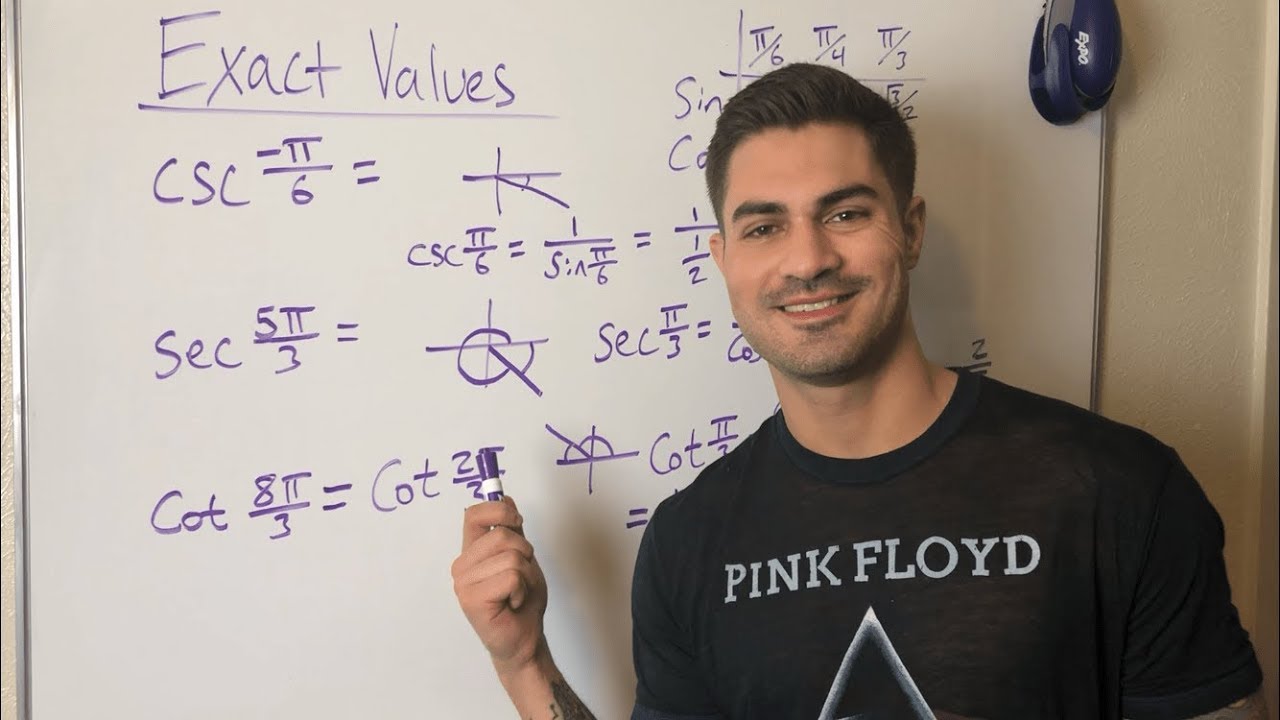Trigonometry Final Exam Review
TLDRThis video tutorial focuses on solving basic trigonometry problems without the use of a calculator. It covers essential concepts such as converting degrees to radians, understanding coterminal angles, and applying trigonometric identities like SOHCAHTOA. The video also introduces reference triangles and unit circles for determining trigonometric function values, and emphasizes the importance of recognizing the signs of sine, cosine, and tangent in different quadrants. By working through various problems, the viewer is encouraged to pause and attempt solutions independently before comparing their answers to the provided solutions.
Takeaways
- 📐 Convert degrees to radians by multiplying by pi and dividing by 180.
- 🔄 Negative angles represent clockwise rotation, with positive angles for counterclockwise.
- 🔄 Coterminal angles share the same terminal side and can be found by adding or subtracting multiples of 360 degrees.
- 📐 Arc length is calculated by multiplying the angle in radians by the radius of the circle.
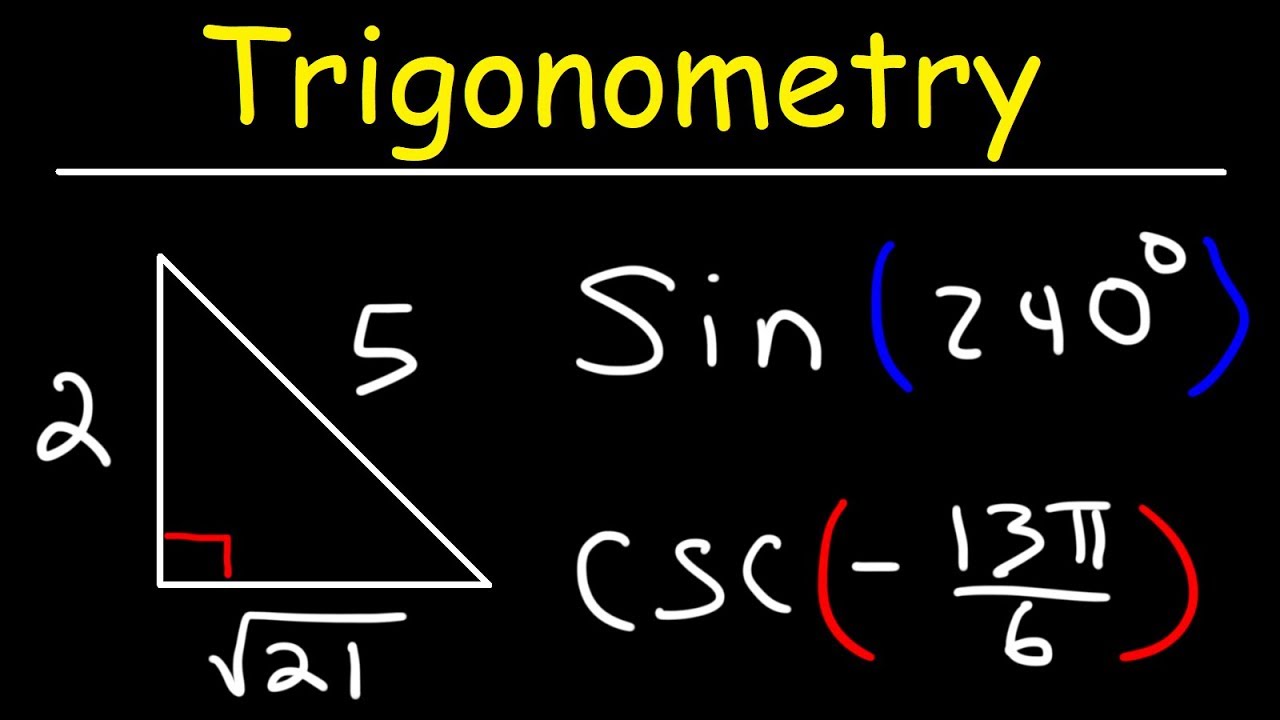
- 📐 The Pythagorean theorem (a^2 + b^2 = c^2) is used to find missing sides in right triangles.
- 📐 Special right triangles (3-4-5, 5-12-13, 7-24-25, 8-15-17, 9-40-41, 11-60-61) have specific ratios that can be scaled.
- 📐 SOHCAHTOA is a mnemonic for sine, cosine, and tangent ratios in right triangles.
- 📐 Reciprocal identities (cosecant = 1/sine, secant = 1/cosine, cotangent = 1/tanget) are useful for solving trigonometric problems.
- 📐 The Pythagorean identities (sine^2 + cosine^2 = 1, 1 + cotangent^2 = cosecant^2, 1 + tangent^2 = secant^2) are essential for advanced trigonometry.
- 📐 The signs of sine, cosine, and tangent in different quadrants can help determine the correct values of trigonometric functions for given angles.
- 📐 The reference angle of an angle can be found by reducing it to an acute angle within the range of 0 to 90 degrees, depending on the quadrant it lies in.
Q & A
How can you convert degrees to radians?
-To convert degrees to radians, you multiply the degree measure by pi and divide by 180. For example, to convert 60 degrees to radians, you would calculate 60 * pi / 180.
What is the significance of coterminal angles?
-Coterminal angles are angles that share the same initial side and terminal side, meaning they have the same position on the coordinate plane. They can be found by adding or subtracting multiples of 360 degrees to the original angle.
How do you find the arc length of a circle?
-The arc length is found by multiplying the radius of the circle by the angle in radians. The formula is arc length = angle (in radians) * radius.
What is the Pythagorean theorem and how is it used in trigonometry?
-The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. It is used in trigonometry to find the missing side lengths in right triangles.
What are the basic trigonometric ratios?
-The basic trigonometric ratios are sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent). These ratios are used to relate the angles of a right triangle to the lengths of its sides.
What are reciprocal identities in trigonometry?
-Reciprocal identities in trigonometry are the relationships between the trigonometric functions and their reciprocals. For example, cosecant is the reciprocal of sine (csc = 1/sin), secant is the reciprocal of cosine (sec = 1/cos), and cotangent is the reciprocal of tangent (cot = 1/tan).
How do you determine the quadrant in which an angle lies?
-An angle's quadrant is determined by its measure relative to the x-axis. Quadrant I angles are between 0 and 90 degrees (0 and π/2 radians), Quadrant II between 90 and 180 degrees (π/2 and π radians), Quadrant III between 180 and 270 degrees (π and 3π/2 radians), and Quadrant IV between 270 and 360 degrees (3π/2 and 2π radians).
What is the reference angle of a given angle?
-The reference angle of a given angle is the acute angle formed with the x-axis by the terminal side of the original angle. It is used to find the values of trigonometric functions for angles outside the first quadrant.
How do you calculate the value of a trigonometric function for an angle in a different quadrant?
-To calculate the value of a trigonometric function for an angle in a different quadrant, you first find the reference angle and then apply the signs of the trigonometric functions for that quadrant. For example, sine is positive in quadrants I and II, cosine is positive in quadrants I and IV, and tangent is positive in quadrants I and III.
What is the relationship between sine and cosine in the context of the unit circle?
-In the context of the unit circle, sine corresponds to the y-coordinate of a point on the circle, and cosine corresponds to the x-coordinate. The values of these functions depend on the quadrant in which the angle lies.
Outlines
🔄 Converting Degrees to Radians and Exploring Angle Measures
The video begins with a step-by-step guide on solving basic trigonometry problems, emphasizing the importance of hands-on practice by pausing the video to attempt problems before viewing the solutions. The initial focus is on converting degrees to radians, using 60 degrees as an example to demonstrate the conversion method that involves multiplying by π/180. This segment further explores various angle measures, including understanding negative angles and their representation in both degrees and radians, as well as introducing concepts like coterminal angles and the significance of direction (clockwise vs. counterclockwise) in determining angle positivity or negativity.
📏 Understanding Arc Length and Trigonometric Ratios
The video progresses to more complex concepts such as calculating the arc length of a circle segment with given angle measures and radii, illustrating the formula involving radians. It then delves into finding sine values using right triangle properties and introduces the SOHCAHTOA mnemonic for remembering trigonometric ratios. The discussion includes special right triangles and their properties, such as the 3-4-5 and 5-12-13 triangles, and explains how to find the missing sides of these triangles using the Pythagorean theorem. This section is essential for understanding how to apply trigonometric ratios to solve problems.
🔍 Exploring Reciprocal Trigonometric Functions and Special Triangles
This segment expands the discussion to reciprocal trigonometric functions like secant, cosecant, and cotangent, explaining how to find their values using the known sides of right triangles. It emphasizes the importance of understanding the relationships between these functions and the basic trigonometric functions (sine, cosine, and tangent). The video also revisits the concept of special right triangles, illustrating how to identify and use them in solving problems, particularly focusing on the 5-12-13 and 7-24-25 triangles.
🌐 Coterminal Angles and Trigonometric Values in Different Quadrants
Focusing on coterminal angles and their properties, this part of the video explains how angles that share the same terminal side have the same trigonometric values, despite having different measures. It provides strategies for finding coterminal angles by adding or subtracting full rotations (360 degrees or 2π radians). The video also covers how to determine the signs of trigonometric functions based on the quadrant in which the angle lies, illustrating the concept with angles in quadrants 1 through 4 and explaining the 'All Students Take Calculus' mnemonic for remembering these signs.
🔄 Revisiting Trigonometric Functions' Properties and Solving Advanced Problems
The video continues to deepen the understanding of trigonometry by revisiting the even-odd properties of trigonometric functions and how they affect the signs of their values. It covers solving advanced problems involving these properties, such as finding the equivalent expressions for given trigonometric functions. This section is crucial for grasping the conceptual underpinnings of trigonometry and provides viewers with tools to tackle trigonometric expressions without relying on a calculator.
🎯 Calculating Tangent and Cotangent Values Using Special Points
This segment teaches how to find the exact values of tangent and cotangent using points on the terminal side of an angle. It delves into the geometric interpretation of trigonometric functions, explaining how to construct right triangles in specific quadrants based on given points. The discussion includes finding trigonometric values using these triangles and the significance of understanding the quadrant system for solving trigonometry problems accurately.
🔎 Identifying Quadrants Based on Trigonometric Function Signs
The video concludes with a focus on determining the quadrant in which an angle lies based on the signs of its sine and cosine values. It reinforces the concept of 'All Students Take Calculus' for remembering which trigonometric functions are positive in each quadrant. This final segment emphasizes the practical application of trigonometric concepts in solving problems and how to utilize mnemonic devices to aid in remembering the relationships between angles, trigonometric functions, and quadrants.
Mindmap
Keywords
💡Trigonometry
💡Degrees to Radians
💡Coterminal Angles
💡Sine Function
💡Pythagorean Theorem
💡Trigonometric Identities
💡Unit Circle
💡Reference Angle
💡Special Right Triangles
💡Trigonometric Graphs
Highlights
The video focuses on solving basic trigonometry problems, providing a methodical approach to tackle them.
The technique to convert degrees to radians is by multiplying by pi and dividing by 180.
To simplify trigonometric expressions, it's important to cancel out common factors in fractions.
The concept of coterminal angles is introduced, which are angles that share the same terminal side on a unit circle.
The video explains how to find the arc length using the formula relating angle in radians and the radius of a circle.
The use of the Pythagorean theorem is demonstrated to find the hypotenuse of a right triangle given the lengths of the other two sides.
The video introduces the concept of special right triangles and their ratios, such as the 3-4-5 triangle.
The SOHCAHTOA mnemonic is explained, which relates the trigonometric functions to the sides of a right triangle.
Reciprocal identities for trigonometric functions are discussed, such as cosecant being 1/sine and secant being 1/cosine.
The video demonstrates how to find the value of tangent using the definition of sine and cosine in a right triangle.
The concept of reference angles is introduced, which are acute angles used to find the values of trigonometric functions for larger angles.
The video explains how to find the exact value of trigonometric functions like cosine 60 using reference triangles like the 30-60-90 triangle.
The video provides a method to find the value of trigonometric functions without a calculator using unit circles and special triangles.
The video emphasizes the importance of understanding the signs of trigonometric functions in different quadrants.
The video concludes with a comprehensive explanation of how to find the reference angle of any given angle and its practical applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: