Signs of Trigonometric Function Values
TLDRThis video script delves into the signs of trigonometric function values based on the quadrants in which angles terminate. It explains how the coordinates of a point on the terminal side of an angle determine the signs of sine, cosine, and tangent. The video also covers reciprocal trigonometric functions, highlighting that their signs match those of the original functions. Through examples, the script teaches viewers how to identify an angle's quadrant by analyzing the signs of trigonometric function values.
Takeaways
- 📍 The signs of trigonometric function values depend on the quadrant in which the angle terminates.
- 📈 Trigonometric function definitions involve the coordinates (x, y) of a point on the terminal side of an angle and the radius r.
- ✅ The radius r is always positive, while the coordinates (x, y) can be positive or negative depending on the quadrant.
- 🔢 In Quadrant I (Q1), both x and y coordinates are positive; in Quadrant II (Q2), x is negative and y is positive; in Quadrant III (Q3), both are negative; and in Quadrant IV (Q4), x is positive and y is negative.
- 📶 For sine and cosine functions, the sign of the function value depends on the y-coordinate for sine and the x-coordinate for cosine.
- 🌀 In Quadrant I, both sine and cosine are positive; in Quadrant II, cosine is negative and sine is positive; in Quadrant III, both are negative; and in Quadrant IV, cosine is positive and sine is negative.
- 🔽 The sign of the tangent function depends on both x and y coordinates, with positive tangent in Quadrants I and III, and negative in Quadrants II and IV.
- 🔄 Reciprocal trigonometric functions (cosecant, secant, and cotangent) have the same sign as their corresponding basic functions (sine, cosine, and tangent).
- 💡 To determine the quadrant of an angle, analyze the signs of the trigonometric functions and match them with the quadrant characteristics.
- 📌 Examples provided in the script demonstrate how to identify the quadrant of an angle based on the signs of sine, cosine, and tangent, as well as their reciprocals.
Q & A
How do the signs of trigonometric function values depend on the quadrants where the angles terminate?
-The signs of trigonometric function values depend on the coordinates of the point on the terminal side of the angle. In Quadrant I, both sine and cosine are positive; in Quadrant II, cosine is negative and sine is positive; in Quadrant III, both sine and cosine are negative; and in Quadrant IV, cosine is positive and sine is negative.
What is the significance of the radius in the context of trigonometric functions?
-The radius is a constant value that represents the distance from the origin to the point on the terminal side of the angle. It is always positive and is used as the denominator in the definitions of sine, cosine, and tangent functions.
How do the signs of the coordinates (x and y) affect the sign of the sine function?
-The sign of the sine function depends on the y-coordinate of the point on the terminal side of the angle. If the y-coordinate is positive, the sine value is positive; if it is negative, the sine value is negative.
What determines the sign of the cosine function?
-The sign of the cosine function depends on the x-coordinate of the point on the terminal side of the angle. If the x-coordinate is positive, the cosine value is positive; if it is negative, the cosine value is negative.
How does the tangent function's sign vary across different quadrants?
-The sign of the tangent function depends on both the x and y coordinates. In Quadrant I, tangent is positive (positive/positive); in Quadrant II, tangent is negative (positive/negative); in Quadrant III, tangent is positive (negative/negative); and in Quadrant IV, tangent is negative (negative/positive).
What is the relationship between the signs of reciprocal trigonometric functions and their corresponding original functions?
-Reciprocal trigonometric functions always have the same sign as their corresponding original functions. For example, if the cosine (and thus secant) is negative, its reciprocal, the cosecant, will also be negative.
How can you determine the quadrant of an angle if you know the sine is positive and the secant is negative?
-If the sine is positive, the angle must be in Quadrant I or II. If the secant (reciprocal of cosine) is negative, the cosine must be negative, which places the angle in Quadrant II.
What is the significance of the quadrant in which an angle terminates for the tangent function?
-The quadrant in which an angle terminates determines the sign of the tangent function. Tangent will be positive in Quadrants I and III, where x and y have the same sign, and negative in Quadrants II and IV, where x and y have opposite signs.
How can you identify the quadrant of an angle if the tangent is positive and the cosecant is negative?
-If the tangent is positive, the angle must be in Quadrant I or III. If the cosecant (reciprocal of sine) is negative, the sine must be negative, which places the angle in Quadrant III.
What are the key points to remember when analyzing the signs of trigonometric functions?
-Key points include associating sine with the y-coordinate and cosine with the x-coordinate, understanding that tangent depends on both x and y coordinates, and knowing that reciprocal functions always have the same sign as their corresponding functions.
Can you provide an example of determining an angle's quadrant based on the signs of its trigonometric functions?
-If the sine of an angle is positive and the cosine is negative, the angle must be in Quadrant II. Similarly, if the tangent is positive and the cotangent (reciprocal of tangent) is negative, the angle must be in Quadrant I.
Outlines
📊 Understanding Trigonometric Function Signs
This paragraph introduces the concept of trigonometric function values and how their signs are determined by the quadrant in which the angle terminates. It explains the definitions of trigonometric functions using coordinates (x, y) and the radius (r) from the origin. The discussion includes the signs of coordinates in each quadrant (Q1-Q4) and how these signs affect the sine, cosine, and tangent functions. The key takeaway is that the sign of sine depends on the y-coordinate and cosine on the x-coordinate, with tangent's sign depending on both.
🔄 Reciprocal Trigonometric Functions and Their Signs
This section delves into the signs of reciprocal trigonometric functions, explaining that the signs of reciprocals always match the original function. It provides a straightforward method for determining the signs of functions like secant (reciprocal of cosine) and cotangent (reciprocal of tangent) based on the known signs of cosine and tangent, respectively. The summary emphasizes the algebraic principle that reciprocals maintain the same sign, simplifying the process of identifying the quadrant of an angle based on the signs of its trigonometric function values.
🧩 Identifying Quadrants with Trigonometric Function Signs
The paragraph focuses on applying the knowledge of trigonometric function signs to identify the quadrant in which an angle terminates. It uses two examples to illustrate the process: one with sine and secant, and another with tangent and cosecant. The explanation walks through the logical steps of deducing the quadrant by considering the signs of the functions and their associated coordinates. The conclusion is that by matching the conditions of both sine and cosine (or tangent and cotangent), one can accurately determine the quadrant of the angle.
Mindmap
Keywords
💡Trigonometric Functions
💡Quadrants
💡Coordinates
💡Radius
💡Sine Function
💡Cosine Function
💡Tangent Function
💡Reciprocal Functions
💡Signs of Functions
💡Angle Termination
Highlights
Trigonometric function values can be positive or negative depending on the quadrant of the angle.
Trigonometric function definitions involve coordinates of a point on the terminal side of an angle.
The radius (r) is always positive in the context of trigonometric functions.
Coordinates (x and y) can be positive or negative depending on the quadrant.
In quadrant one, both x and y coordinates are positive.
In quadrant two, x is negative and y is positive.
In quadrant three, both x and y coordinates are negative.
In quadrant four, x is positive and y is negative.
The sign of sine depends on the y-coordinate of the point.
The sign of cosine depends on the x-coordinate of the point.
Tangent's sign depends on both x and y coordinates.
Tangent is positive in quadrants where x and y have the same sign (1 and 3).
Tangent is negative in quadrants where x and y have different signs (2 and 4).
Reciprocal functions have the same sign as their original functions.
Secant is positive when cosine is positive, and negative when cosine is negative.
Cosecant is positive when sine is positive, and negative when sine is negative.
Identifying the quadrant of an angle involves analyzing the signs of its trigonometric functions.
If sine is positive, the angle terminates in quadrants where y is positive (1 or 2).
If cosine is negative, the angle terminates in quadrants where x is negative (2 or 3).
Combining the signs of sine and secant can help determine the quadrant of an angle.
Combining the signs of tangent and cosecant can also determine the quadrant of an angle.
Angle theta terminates in quadrant two if sine is positive and secant is negative.
Angle theta terminates in quadrant three if tangent is positive and cosecant is negative.
Transcripts
Browse More Related Video

Trig - 0.7 Trig Functions of Any Angle
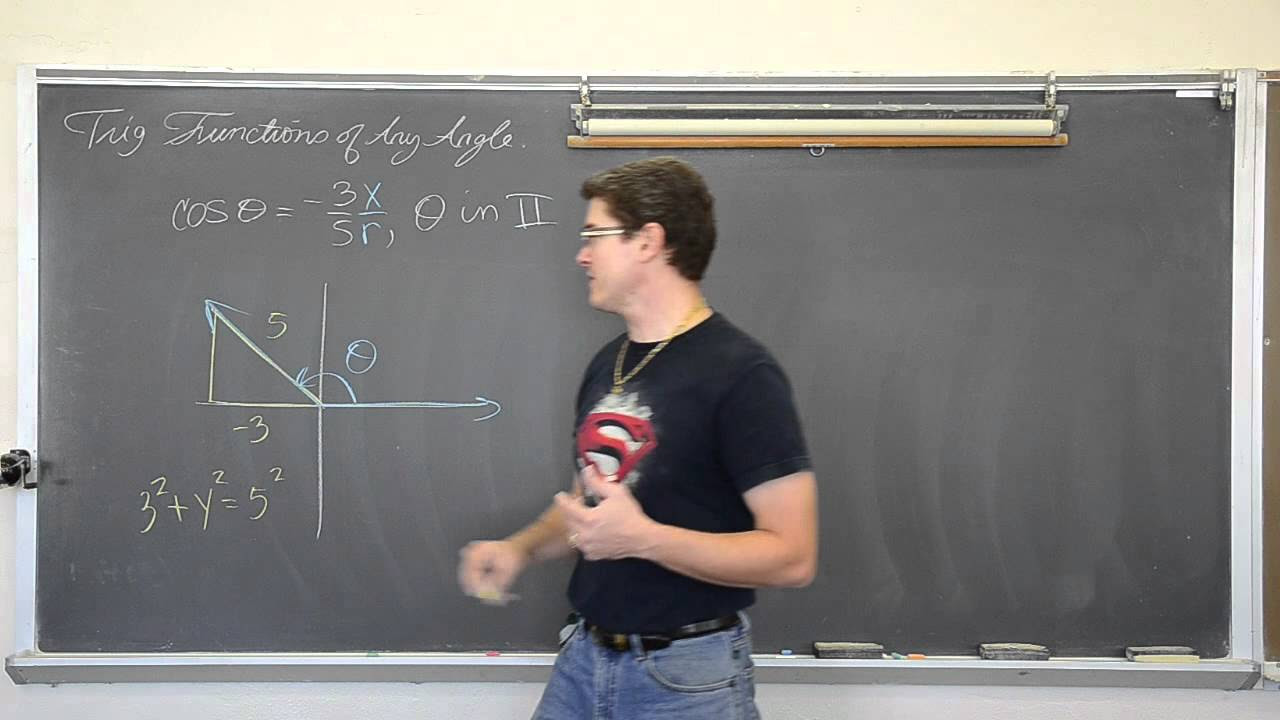
Trigonometric Functions of Any Angle

Trigonometry: How to use the ASTC Rule | The Quadrant | CAST

How To Use Reference Angles to Evaluate Trigonometric Functions

Trigonometry - The signs of trigonometric functions

Reciprocal Identities in Trigonometry (Precalculus - Trigonometry 9)
5.0 / 5 (0 votes)
Thanks for rating: