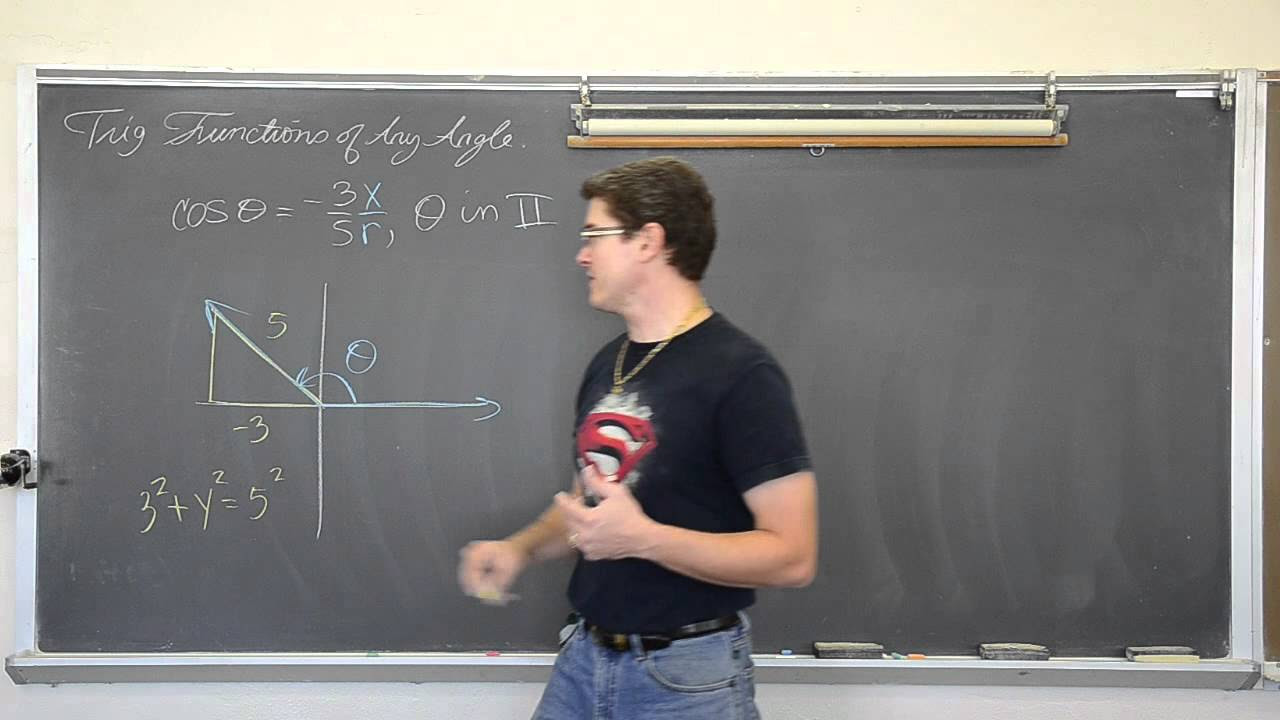Trigonometry - The signs of trigonometric functions
TLDRIn this informative video, the presenter introduces a mnemonic tool for understanding the signs of trigonometric functions based on their quadrant positions. By using the phrase 'all students take calculus,' the video simplifies the process of determining whether sine, cosine, tangent, and their reciprocals are positive or negative in each quadrant. The method is demonstrated with examples, showing how to deduce the quadrant of an angle based on the signs of its trigonometric functions, providing a practical approach to solving trigonometry problems.
Takeaways
- 📚 The video introduces a mnemonic tool for remembering the signs of trigonometric functions based on their quadrant locations.
- 📈 Trigonometric functions like sine and cosine have positive or negative values depending on the quadrant in which their angles reside.
- 🔢 For example, sine of 23 degrees is positive because 23 degrees lies in the first quadrant.
- 🌟 All trigonometric functions are positive in the first quadrant.
- 📌 In the second quadrant, sine and its reciprocal (cosecant) are positive, while tangent and cosine are negative.
- 🔄 The mnemonic 'All Students Take Calculus' helps remember which functions are positive in each quadrant, with the first letter of each word corresponding to a quadrant.
- 🤔 To determine an angle's quadrant, use the signs of trigonometric functions: if sine is negative, the angle is in the third or fourth quadrant; if tangent is positive, it's in the first or third quadrant.
- 📊 If an angle's sine is negative and tangent is positive, the angle must be in the third quadrant.
- 🚫 Be cautious with reciprocal functions like cosecant, which is the reciprocal of sine and shares its sign.
- 📈 If cosine is negative and cosecant (reciprocal of sine) is positive, the angle must be in the second quadrant.
- 💡 Writing down the mnemonic and quadrant signs can serve as a quick reference for determining the signs of trigonometric functions.
Q & A
What is the main topic of the video?
-The main topic of the video is understanding the signs of different trigonometric functions using a mnemonic tool.
How can you determine if a trigonometric function like sine or cosine is positive or negative?
-You can determine if a trigonometric function is positive or negative by knowing in which quadrant the angle lies.
What are the mnemonic letters used in the video to remember the signs of trigonometric functions in each quadrant?
-The mnemonic letters used are A for first quadrant (All positive), S for second quadrant (Sine positive, others negative), T for third quadrant (Tangent and its reciprocal positive), and C for fourth quadrant (Cosine and its reciprocal positive).
What does the mnemonic 'all students take calculus' represent?
-The mnemonic 'all students take calculus' helps remember the signs of trigonometric functions in each quadrant, with 'all' for quadrant one, 'students' for quadrant two, 'take' for quadrant three, and 'calculus' for quadrant four.
How can you use the information about the sign of sine to narrow down the quadrant of an angle?
-If sine is negative, the angle must be in the second or third quadrant, as sine is positive in the first and fourth quadrants.
What is the relationship between the signs of sine and its reciprocal, cosecant?
-Cosecant is the reciprocal of sine, so they have the same sign. If sine is positive, cosecant is positive, and if sine is negative, cosecant is negative.
How does the sign of tangent help in determining the quadrant of an angle?
-If tangent is positive, the angle is in the first or third quadrant, as tangent is negative in the second and fourth quadrants.
What happens if you know the sign of both cosine and cosecant for an angle?
-If cosine is negative and cosecant (the reciprocal of sine) is positive, the angle must be in the second quadrant, as cosine is negative there and sine (and hence cosecant) is positive.
How can the mnemonic tool be used in practice for a quick test or problem-solving?
-The mnemonic tool can be quickly sketched on a piece of paper to help remember the signs of trigonometric functions in each quadrant, aiding in solving problems on the spot.
What is the purpose of the mnemonic tool in learning trigonometry?
-The mnemonic tool helps in memorizing the signs of trigonometric functions in different quadrants, providing a quick reference and enhancing understanding of their behavior in various scenarios.
Outlines
📚 Understanding Trigonometric Signs with a Mnemonic
This paragraph introduces a mnemonic tool for remembering the signs of trigonometric functions based on their quadrant locations. It explains how to determine if functions like sine, cosine, and tangent are positive or negative by identifying the quadrant in which the angle resides. The mnemonic 'All Students Take Calculus' is introduced to help remember which functions are positive in each quadrant (1: all positive, 2: sine and cosecant, 3: tangent and cotangent, 4: cosine and secant). An example is provided to illustrate how to use this information to deduce the quadrant of an angle based on the signs of its sine and tangent values.
🔍 Applying the Mnemonic to Determine Angle Quadrants
The second paragraph expands on the mnemonic by discussing its application to all trigonometric functions, including their reciprocal identities. It emphasizes that cosecant, being the reciprocal of sine, shares the same sign as sine. The paragraph then uses the mnemonic to identify the quadrant of an angle based on the positive sine and positive cosecant conditions, leading to the conclusion that the angle is in the second quadrant. The summary encourages using the mnemonic as a quick reference for understanding the signs of trigonometric functions and provides a link to more resources.
Mindmap
Keywords
💡Trigonometric Functions
💡Quadrants
💡Signs
💡Mnemonic
💡Sine
💡Cosine
💡Tangent
💡Reciprocal Identities
💡Unit Circle
💡Angle
💡Mathematics
Highlights
The video introduces a neat tool for memorizing the signs of trigonometric functions.
Understanding the signs of sine and cosine helps in determining the quadrant of an angle.
All trigonometric functions are positive in the first quadrant.
In the second quadrant, sine is positive, while tangent and cosine are negative.
Tangent and its reciprocal are positive in the third quadrant.
Cosine and its reciprocal, secant, are positive in the fourth quadrant.
A mnemonic for remembering the signs is 'all students take calculus', with each word corresponding to a quadrant.
If sine is negative, the angle must be in the third or fourth quadrant.
Positive tangent indicates the angle is in the first or third quadrant.
The combination of negative sine and positive tangent places the angle in the third quadrant.
Cosine is negative and cosecant is positive, which helps to identify the quadrant of the angle.
Negative cosine rules out the first and fourth quadrants.
Cosecant, being the reciprocal of sine, shares the same sign as sine.
The angle is in the second quadrant if cosine is negative and cosecant is positive.
The video demonstrates a practical application of the mnemonic for quick problem-solving.
The method can be sketched out for quick reference during tests or problem-solving.
The video encourages viewers to visit a website for more educational content.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: