How To Remember The Unit Circle Fast!

The Organic Chemistry Tutor

2 Aug 201812:43

EducationalLearning

32 Likes 10 Comments

TLDRThis video tutorial offers a comprehensive guide on memorizing the unit circle in radians, breaking it into equal parts to understand angles and their corresponding values. It explains the relationship between radians and degrees, and how to use the unit circle to evaluate trigonometric functions by identifying the correct x and y values for various angles. The video simplifies the process with clear examples and conversions, making it an engaging and informative resource for learning trigonometry.

Takeaways

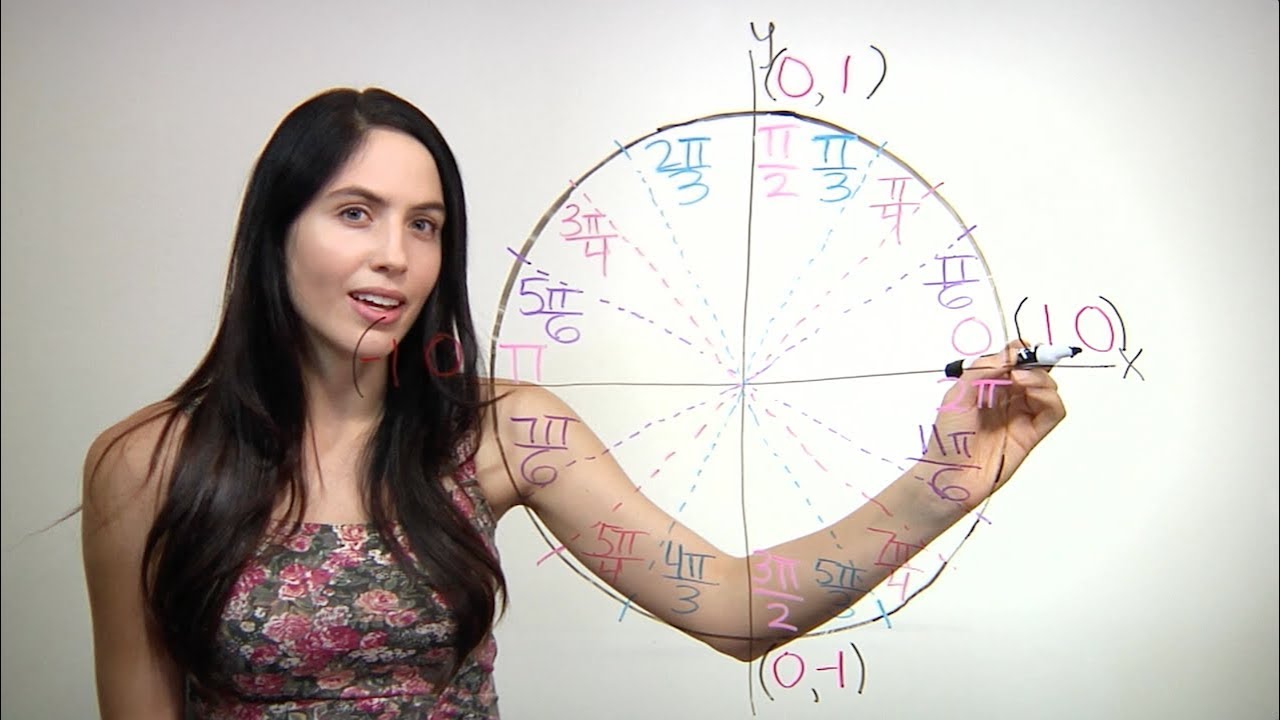
📐 Understanding the unit circle starts with knowing the angles in radians: 0 degrees, π (half circle), π/2 (quarter circle), and multiples thereof.
🔢 The unit circle is divided into eight equal parts, each representing angles like π/4, π/2, 3π/4, and multiples of π/4 up to 2π, which is equivalent to zero degrees again.
📈 To find angles in smaller increments, like π/6, the circle is further divided, and angles are expressed in terms of π and simplified where possible.
🌟 The values on the x-axis and y-axis of the unit circle correspond to the cosine and sine of the respective angles, with the radius being 1.
🔄 Quadrants of the unit circle are numbered and characterized by the signs of their coordinates: Q1 (+,+), Q2 (-,+), Q3 (-,-), Q4 (+,-).
📊 In quadrant one (top right), both x and y are positive; in quadrant two (top left), x is negative and y is positive; in quadrant three (bottom left), both are negative; in quadrant four (bottom right), x is positive and y is negative.
🧭 To find the values for angles like π/3 and π/4, start at the origin (0,0) and move along the unit circle to the corresponding angle, noting the x and y coordinates.
🔄 Reflecting the values across the y-axis helps find the coordinates for angles in other quadrants, with the main difference being the sign of the coordinates.
📐 To convert radians to degrees, multiply the radian value by 180/π, allowing for quick translation of radian angles to their degree equivalents.
📈 The unit circle can be used to evaluate trigonometric functions by locating the angle and using the corresponding x or y value to find sine, cosine, or tangent.

Q & A

What is the relationship between a full circle and radians?
-A full circle is equivalent to 2π radians.
How can you express half a circle in radians?
-Half a circle is π radians.
What are the eight equal parts of the unit circle when divided in radians?
-The eight equal parts are π/4, 2π/4 (π/2), 3π/4, 4π/4 (π), 5π/4, 6π/4 (3π/2), 7π/4, and 8π/4 (2π).
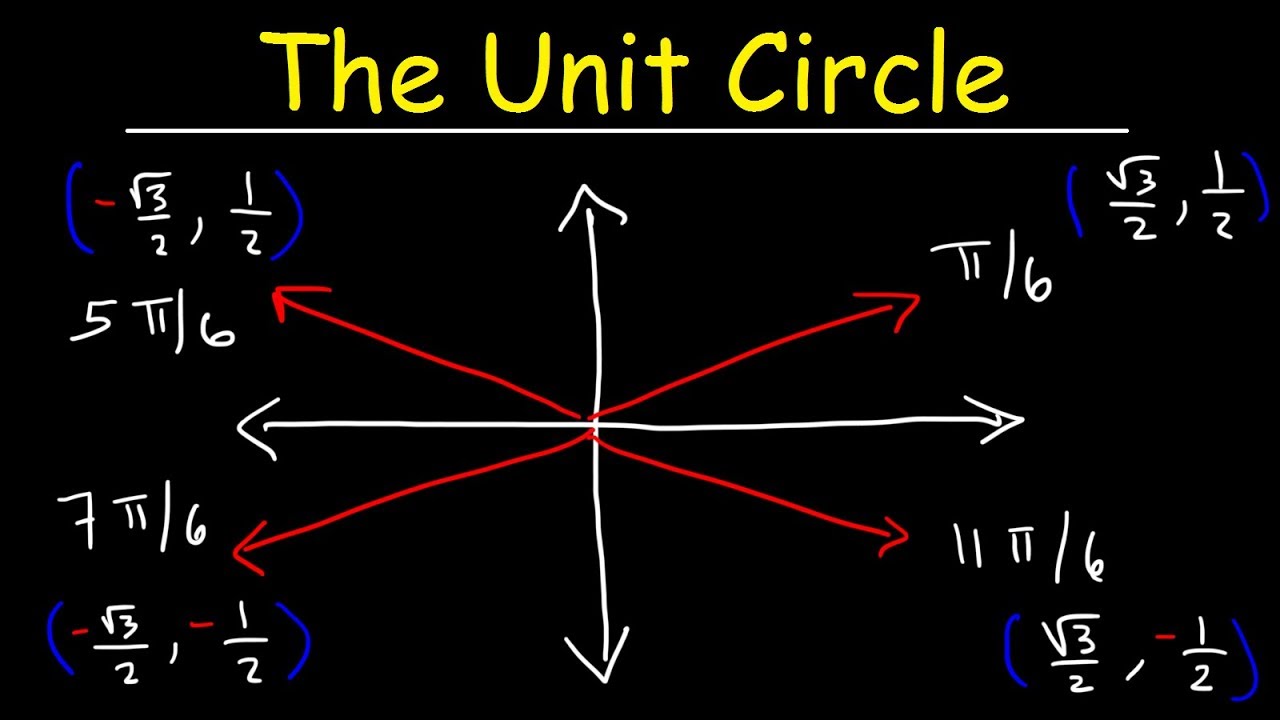
How can you find the angles that are equivalent to π/3 and π/2 when reduced?
-2π/6 reduces to π/3, and 3π/6 is equivalent to π/2.
What are the x and y values on the unit circle for quadrant one?
-In quadrant one, x is positive and increases from 0 to 1, while y increases from 0 to 1.
How do the x and y values change when moving from quadrant one to quadrant two?
-In quadrant two, x becomes negative while y remains positive.
What is the method to evaluate sine and cosine functions using the unit circle?
-For sine, you use the y value, and for cosine, you use the x value at the corresponding angle on the unit circle.
How can you calculate the tangent function using the unit circle?
-The tangent function is calculated as the y value divided by the x value at the given angle on the unit circle.
What is the conversion factor from radians to degrees?
-To convert from radians to degrees, multiply the radian measure by 180/π.
How do you find the angle measures in degrees for π/6, π/4, and 5π/6?
-π/6 is 30 degrees, π/4 is 45 degrees, and 5π/6 is 150 degrees.
What are the key points to remember when memorizing the unit circle?
-Memorize the angles in radians, the corresponding x and y values for each quadrant, and how to evaluate trigonometric functions using these values.

Outlines

00:00

📐 Understanding the Unit Circle and Radian Measures

This paragraph introduces the concept of the unit circle and the importance of understanding radian measures. It explains the relationship between degrees and radians, highlighting the key angles such as 0, π/2, π, 3π/2, and 2π. The speaker then breaks down the unit circle into eight equal parts, detailing the radian measures for each segment. The paragraph further discusses the angles that are located on the x-axis and y-axis of the unit circle, providing a foundation for understanding the unit circle's role in trigonometry.

05:00

🔄 Reflecting Values Across Quadrants

The second paragraph delves into the reflection of values across the y-axis and how it affects the signs of the coordinates in different quadrants. It explains the values for quadrants one through four, detailing the x and y coordinates for specific angles such as π/3, π/4, and 5π/6. The speaker emphasizes the pattern of reflection and sign change when moving from one quadrant to another, providing a clear understanding of how to fill in the unit circle with the correct values based on the quadrant's position.

10:01

📈 Evaluating Trigonometric Functions Using the Unit Circle

In the final paragraph, the focus shifts to applying the knowledge of the unit circle to evaluate trigonometric functions. The speaker demonstrates how to use the unit circle to find the values of sine, cosine, and tangent for given angles. By locating the angle on the unit circle and selecting the appropriate x or y value, one can determine the trigonometric function's value. The paragraph concludes with a brief mention of how to convert radian measures to degrees, providing a comprehensive guide on utilizing the unit circle for trigonometric evaluations.

Mindmap

Keywords

💡Unit Circle

The unit circle is a circle with a radius of 1 centered at the origin (0,0) in the coordinate plane. It is a fundamental concept in trigonometry, used to define and visualize trigonometric functions. In the video, the unit circle is used to memorize and understand angles in radians and their corresponding trigonometric values.

💡Radians

Radians are a measure of angles in the context of a circle. One radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. Radians are used instead of degrees in many mathematical and scientific contexts due to their convenient relationship with the circle's dimensions. In the video, the unit circle is divided into various radian measures to help memorize the angles and their positions.

💡Trigonometric Functions

Trigonometric functions, namely sine, cosine, and tangent, are mathematical functions that describe the relationship between the angles and sides of a right triangle or, more generally, the angles and coordinates on the unit circle. These functions are essential in solving various problems in geometry, physics, and engineering. The video demonstrates how to use the unit circle to evaluate these functions at different angles.

💡Quadrants

The quadrants are the four equal regions of the coordinate plane formed by the intersection of the x-axis and y-axis. Each quadrant is defined by the signs of the x (horizontal) and y (vertical) coordinates. Quadrants are used to understand the position of points and the signs of coordinates in various mathematical and geometric contexts. In the video, the unit circle is used to explain the signs of trigonometric function values in each quadrant.

💡X-axis and Y-axis

The x-axis and y-axis are the two perpendicular lines that intersect at the origin in the coordinate plane. They serve as the basis for the Cartesian coordinate system and are used to define the position of points and the graph of functions. In the context of the unit circle, the x-axis and y-axis represent the horizontal and vertical coordinates of points on the circle, which correspond to the values of trigonometric functions.

💡Sine Function

The sine function is a trigonometric function that relates the ratio of the length of the side opposite an angle in a right triangle to the length of the hypotenuse. In the context of the unit circle, sine corresponds to the y-coordinate of a point on the circle at a given angle. The video demonstrates how to use the unit circle to find the sine values for different angles.

💡Cosine Function

The cosine function is a trigonometric function that relates the ratio of the length of the adjacent side to the hypotenuse in a right triangle or, equivalently, the x-coordinate of a point on the unit circle at a given angle. It is used to determine the horizontal coordinate of a point on the unit circle corresponding to a specific angle. The video explains how to use the unit circle to find the cosine values for various angles.

💡Tangent Function

The tangent function is a trigonometric function that defines the ratio of the sine to the cosine of an angle. In the context of the unit circle, the tangent is the ratio of the y-coordinate to the x-coordinate of a point on the circle at a given angle. It is used to determine the slope of the line from the origin to a point on the unit circle. The video demonstrates how to calculate tangent values using the unit circle.

💡Conversion from Radians to Degrees

The conversion from radians to degrees is a process of changing the measure of an angle from the unit of radians to degrees. Since one full circle is 2π radians, and 360 degrees, the conversion factor is 180/π. This conversion is essential for many mathematical and scientific applications where angles are expressed in degrees. The video provides a method to convert radian measures to degrees to understand the angles in more familiar terms.

💡Memorization

Memorization is the process of committing information to memory for later recall. In the context of the video, memorization is used to remember the angles of the unit circle in radians and their corresponding trigonometric values. The video provides strategies for memorizing these values by breaking down the unit circle and associating them with the signs in different quadrants.

💡Trigonometric Values

Trigonometric values are the numerical results obtained from applying trigonometric functions to specific angles. These values represent the ratios of sides in a right triangle or the coordinates on the unit circle. The video focuses on memorizing and understanding the trigonometric values for angles in radians as they relate to the unit circle.

Highlights

The video discusses memorizing the unit circle and understanding angles in radians.

A full circle is 2π radians, and half a circle is π radians.

The unit circle is broken into eight equal parts for easier memorization.

Angles such as π/4, π/2, and 3π/2 are simplified and related to their equivalent fractions.

The video explains how to find angles in radians by reducing them to simpler forms.

Values on the x-axis and y-axis of the unit circle are discussed, with x being 1 on the right and -1 on the left, and y being 1 on top and -1 at the bottom.

The four quadrants of the unit circle are defined, with their respective x and y sign characteristics.

The method for finding x and y values for angles like π/3, π/4, and π/6 in quadrant one is explained.

The video demonstrates how to find values in other quadrants by reflecting those from quadrant one across the y-axis.

Conversion of radian values to degrees is detailed, with π being equal to 180 degrees.

A method for quickly populating angle measures in degrees within the unit circle is provided.

The video concludes with a demonstration of how to use the unit circle to evaluate trigonometric functions.

Sine, cosine, and tangent functions are evaluated using specific angles and their corresponding x and y values on the unit circle.

The process of evaluating trig functions is simplified through the use of the unit circle, with examples provided for clarity.

Transcripts

Browse More Related Video

How to Remember the Unit Circle (NancyPi)

The Unit Circle, Basic Introduction, Trigonometry

Trigonometry: Unit Circle

Precalc 4.1-4.4 Review!

CONVERTING DEGREE MEASURE TO RADIAN MEASURE AND VICE VERSA || PRE-CALCULUS

Reciprocal Identities - Evaluating Secant and Cosecant Functions

How To Remember The Unit Circle Fast!

Takeaways

Q & A

What is the relationship between a full circle and radians?

How can you express half a circle in radians?

What are the eight equal parts of the unit circle when divided in radians?

How can you find the angles that are equivalent to π/3 and π/2 when reduced?

What are the x and y values on the unit circle for quadrant one?

How do the x and y values change when moving from quadrant one to quadrant two?

What is the method to evaluate sine and cosine functions using the unit circle?

How can you calculate the tangent function using the unit circle?

What is the conversion factor from radians to degrees?

How do you find the angle measures in degrees for π/6, π/4, and 5π/6?

What are the key points to remember when memorizing the unit circle?