Calculus 1 Lecture 5.3: Volume of Solids By Cylindrical Shells Method

The paragraph introduces the cylindrical shells method for calculating the volume of a solid of revolution. It discusses the complexity of using the disk or washer method when revolving around the y-axis, as it would require two different functions. The cylindrical shells method simplifies this by considering the volume in terms of a single function of x, revolving around the y-axis, creating a shape akin to a jello mold with a cavity. The concept involves slicing the volume into infinitesimally thin cylindrical shells and summing their volumes.

This section delves into the specifics of calculating the volume of a cylinder using the cylindrical shells method. It emphasizes that the volume of each cylindrical shell is found by multiplying the area of the cross-section (which is the difference between the areas of the outer and inner circles, πr1^2 - πr2^2) by the height (f(x)) and thickness (the function's value at an arbitrary point within the shell). The process involves integrating this expression over the interval [a, b] to find the total volume.

The paragraph focuses on deriving the general formula for the cylindrical shells method. It simplifies the expression for the volume of a single shell by factoring out constants and rearranging terms to express the volume in terms of the average radius, height, and thickness of the shell. The resulting formula is 2π times the average radius, times the height, times the thickness, integrated over the interval of x values.

The discussion here is about selecting an appropriate midpoint for the interval when setting up the cylindrical shells. It is clarified that the midpoint, denoted as x_kdot, should be the average of x_k and x_(k-1), which corresponds to the midpoint of the interval. This choice ensures that the height of the shell at the arbitrary point x_kdot can be accurately represented by the function f(x) at that point.

This paragraph explains how to find the exact volume of the solid by taking the limit of the sum of the volumes of the individual shells as the number of shells approaches infinity. It highlights that as the thickness of each shell approaches zero, the sum of the volumes of the shells becomes an integral from the starting point a to the endpoint b of the interval. The integral involves 2π times the function of x (f(x)), representing the volume of each shell, and is evaluated over the interval [a, b].

The focus is on determining the suitability of using the cylindrical shells method when revolving a region around the y-axis. It emphasizes that the method is appropriate when the function is in terms of x, even when revolving around the y-axis. The paragraph also provides an example problem involving the region enclosed by y = √x and x = 4, revolving around the y-axis, and outlines the steps to set up and evaluate the integral to find the volume.

This section clarifies the difference in approach when revolving a region around the x-axis versus the y-axis using the cylindrical shells method. It stresses the importance of ensuring that the function used is in terms of the correct variable: x for the y-axis and y for the x-axis. The paragraph also addresses a common mistake made by students regarding the axis and the variable in terms of which the function should be expressed.

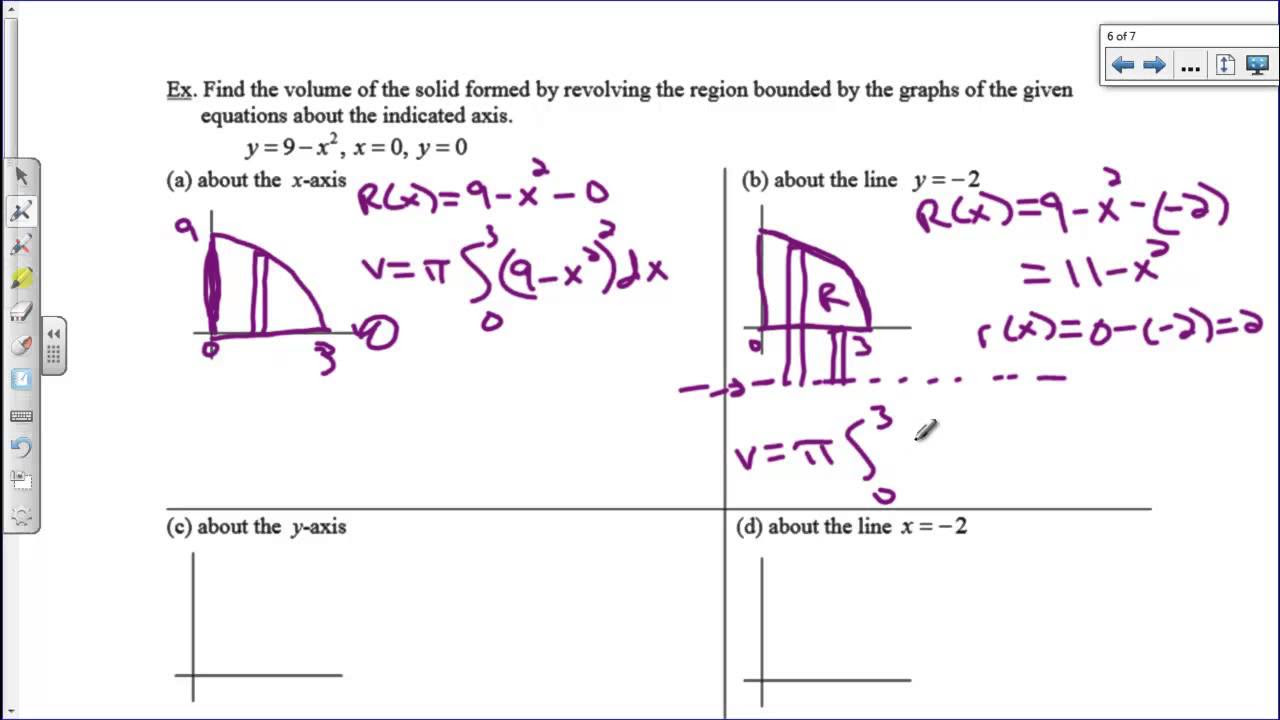
The paragraph provides a detailed walkthrough of setting up and solving an integral using the cylindrical shells method. It involves identifying the correct function to integrate, which in the case of volume between two curves, is the top function minus the bottom function. The integral is then evaluated over the interval [a, b], and the process is illustrated with an example involving functions of x.

This section discusses the decision-making process when choosing between the cylindrical shells and washers methods for finding volumes. It points out that while both methods can be used in many cases, the shells method is often simpler when revolving around the y-axis, as it requires the function to be in terms of x. The washers method, which requires functions in terms of y when revolving around the y-axis, can be more complex due to the need to solve for y, making it less desirable in certain scenarios.

The final paragraph emphasizes the importance of setting up the problem correctly when using the cylindrical shells method. It discusses the process of determining the interval of integration and identifying which function is on top. The paragraph also touches on the common pitfalls, such as obtaining a negative volume, which is not possible in these calculations. It concludes by encouraging students to practice and become comfortable with the setup process, as it is crucial for successfully applying the cylindrical shells method.