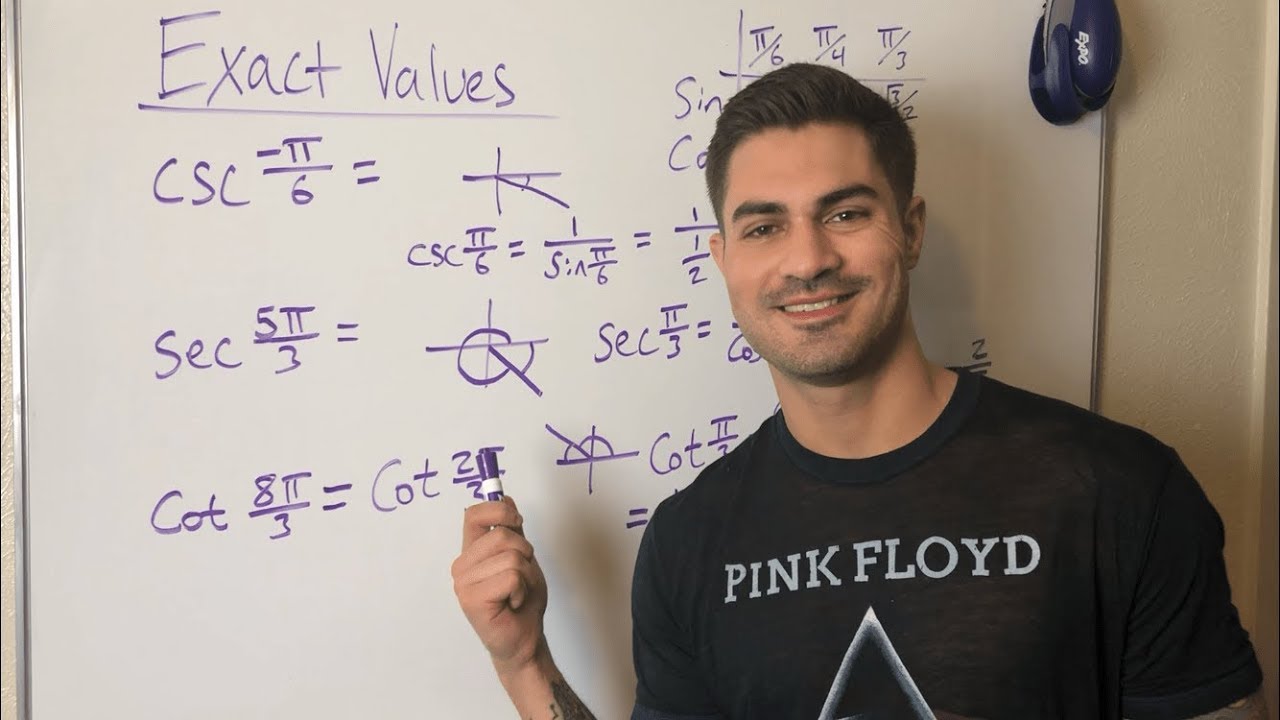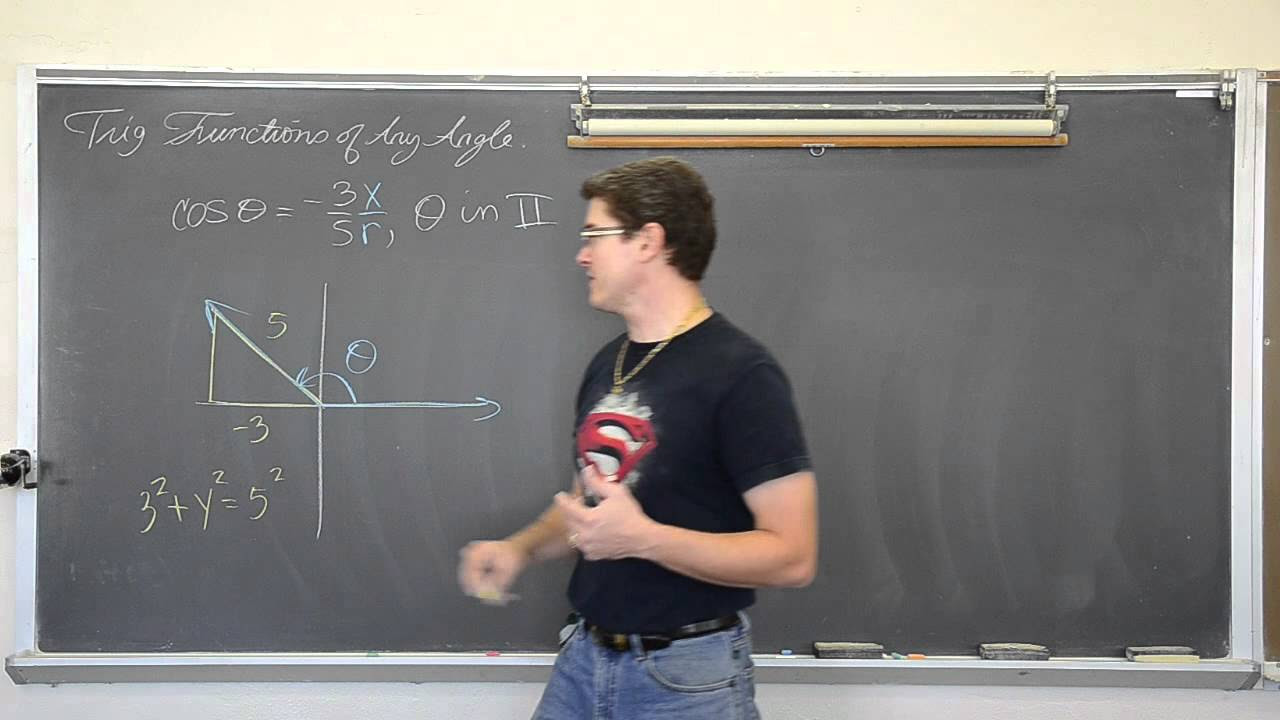Stop memorizing the unit circle
TLDRThe speaker argues against the necessity of memorizing the entire unit circle for trigonometry, suggesting that understanding the first quadrant, reference angles, and coterminal angles is sufficient. By knowing these concepts, one can solve trigonometric problems more efficiently without relying on memorization. The speaker demonstrates this through examples, emphasizing that the unit circle is essentially a repetition of the first quadrant in different orientations, and that mastering graphing and understanding quadrant signs is key to solving problems.
Takeaways
- 🚫 Avoid memorizing the entire unit circle, as it is unnecessary and can be easily forgotten.
- 📍 Focus on understanding the first quadrant and the concepts of reference and coterminal angles for solving problems efficiently.
- 📈 Memorizing the unit circle can lead to confusion, especially when dealing with negative angles or angles larger than 2π.
- 🔄 Knowing the first quadrant allows you to evaluate any trigonometric function using the unit circle.
- 🔢 Reference angles are the acute angles formed between the terminal side of an angle and the x-axis.
- 🌐 Coterminal angles have the same initial and terminal sides but different measures, differing by multiples of 2π.
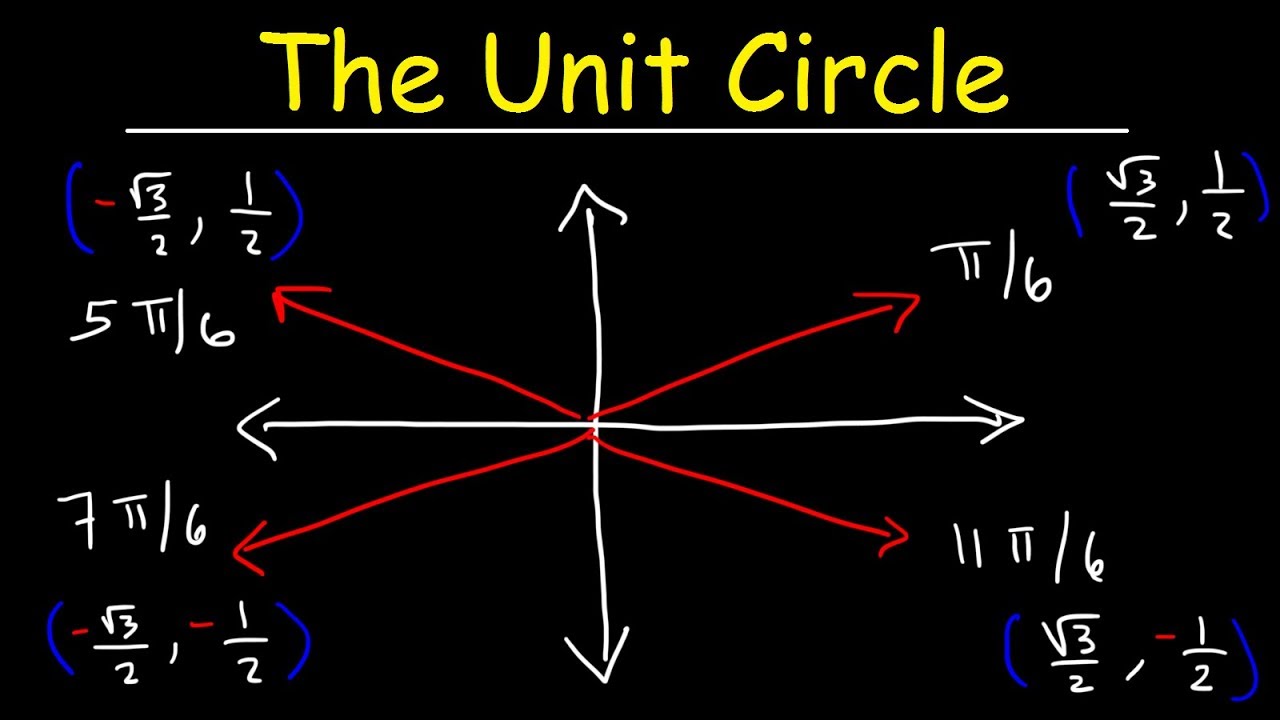
- 🖼️ Visualize angles on the unit circle by breaking them down into parts and identifying their positions relative to the quadrants.
- 🧭 Use the quadrants to determine the sign of the trigonometric function values (positive or negative).
- 🔄 For negative angles, remember that moving counterclockwise is considered positive, while moving clockwise is negative.
- 📊 Practice is key to becoming proficient in identifying angles and their corresponding trigonometric values without memorizing the entire unit circle.
- ✅ The main goal is to understand how to graph any angle and find its coterminal and reference angles, rather than memorizing specific points on the unit circle.
Q & A
Why does the speaker argue against memorizing the unit circle?
-The speaker believes that memorizing the unit circle is a waste of time because it contains a lot of information that is not always required, and it can be easily forgotten. Instead, understanding the first quadrant, reference angles, and coterminal angles is more practical for solving trigonometric problems.
What is the main piece of information the speaker suggests one should memorize instead of the entire unit circle?
-The speaker suggests memorizing the first quadrant of the unit circle, as it is the only essential part needed to evaluate trigonometric functions for any given angle.
What are reference angles and coterminal angles, and how do they help in solving trigonometric problems?
-Reference angles are the acute positive angles between the terminal side of an angle and the x-axis, while coterminal angles have the exact same initial and terminal sides. Knowing these concepts allows one to evaluate any trigonometric function using the unit circle without memorizing all the angles and their corresponding values.
How does the speaker approach solving a problem with a negative angle or an angle larger than 2π?
-The speaker uses the concept of coterminal angles and reference angles to determine the equivalent angle between 0 and 2π. They then find the corresponding point in the first quadrant and use the quadrant's characteristics to determine the correct sign for the value.
What is the significance of the first quadrant in the context of the unit circle?
-The first quadrant is significant because it provides the base values for trigonometric functions. By knowing the coordinates in the first quadrant, one can determine the values for other quadrants by understanding the signs of the coordinates in those quadrants.
How does the speaker explain the concept of coterminal angles?
-Coterminal angles are angles that have the same initial and terminal sides but different measures. The difference between their measures is always a multiple of 2π, which represents the number of revolutions around the circle.
What is the speaker's strategy for solving trigonometric problems with angles like sine of 2π/3?
-The speaker finds the reference angle by determining the acute angle from the terminal side to the x-axis. They then use the coordinates from the first quadrant and adjust for the correct quadrant to find the solution.
How does the speaker handle negative angles in trigonometric problems?
-The speaker breaks down the negative angle into positive angles by adding or subtracting multiples of π. They then find the reference angle and use the first quadrant values, adjusting the sign based on the quadrant where the angle lies.
What is the result of the tangent problem 15π/6 as explained by the speaker?
-The speaker rewrites the angle as a coterminal angle between 0 and 2π, which is π/2. Since π/2 lies on the y-axis, the tangent (y/x) is undefined, resulting in an undefined value for the problem.
What is the speaker's advice for students learning trigonometry?
-The speaker advises students to focus on understanding how to graph angles and find reference and coterminal angles rather than memorizing the entire unit circle. This approach allows for more flexible problem-solving and reduces the risk of confusion caused by memorizing too much information.
How does the speaker describe the relationship between the unit circle and the first quadrant?
-The speaker describes the unit circle as a reproduction of the first quadrant, with the other quadrants derived by reflecting the first quadrant across the axes and changing the signs of the coordinates accordingly.
Outlines
📚 Unnecessary Memorization of the Unit Circle
The speaker argues against the common practice of memorizing the entire unit circle for trigonometry. They share their personal experience of initially memorizing it and later realizing its inefficiency. The speaker emphasizes that knowing only the first quadrant, along with understanding reference and coterminal angles, is sufficient to evaluate any trigonometric function. They introduce the concept of reference angles as the acute angle between the terminal side of an angle and the x-axis and coterminal angles as angles with the same initial and terminal sides. The speaker then demonstrates how to solve problems without memorizing the unit circle by using the first quadrant and understanding quadrant properties.
📐 Solving Trigonometric Problems Without Memorization
The speaker continues to elaborate on their method for solving trigonometric problems without memorizing the unit circle. They provide a step-by-step breakdown of how to find the sine of a negative angle and a tangent problem involving coterminal angles. The speaker explains how to graph angles and use quadrant properties to determine the sign of the trigonometric function values. They conclude by reinforcing the message that memorizing the unit circle is not necessary and that understanding graphing and quadrants is a more effective approach to trigonometry.
Mindmap
Keywords
💡Unit Circle
💡Reference Angle
💡Coterminal Angle
💡First Quadrant
💡Trigonometric Functions
💡Memorization
💡Graphing Angles
💡Negative Angles
💡Quadrants
💡Practice
💡Undefined
Highlights
The speaker argues against the necessity of memorizing the unit circle for solving trigonometry problems.
The main point is that knowing the first quadrant and understanding reference and coterminal angles is sufficient.
Memorizing the entire unit circle can be confusing and is often unnecessary for solving problems.
The first quadrant is the most important part of the unit circle to memorize.
Reference angles are acute angles formed between the terminal side of an angle and the x-axis.
Coterminal angles have the same initial and terminal sides but different measures.
The speaker shares personal experience with memorizing the unit circle and its drawbacks.
The method of using the first quadrant and reference angles can solve problems quicker than full memorization.
The speaker provides a step-by-step approach to solving trigonometry problems without memorizing the unit circle.
Negative angles and angles larger than two pi can be approached more efficiently with the speaker's method.
The process of finding the coordinate in the second quadrant using the first quadrant's knowledge is explained.
The speaker demonstrates how to solve a sine problem with 2 pi over 3 using the reference angle method.
A cosine problem with a negative angle is solved, showing how to handle angles in the second quadrant.
The tangent problem with 15 pi over 6 is solved by finding a coterminal angle and using quadrant knowledge.
The unit circle is essentially a reproduction of the first quadrant, with changes in sign for different quadrants.
The speaker emphasizes not to waste time memorizing angles and instead focus on graphing and understanding angles in the first quadrant.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: