Trigonometry For Beginners!
TLDRThis transcript delves into the fundamentals of right triangle trigonometry, explaining the SOHCAHTOA mnemonic to define sine, cosine, and tangent in terms of the triangle's sides. It demonstrates how to solve for missing sides using the Pythagorean theorem and how to calculate the six trigonometric functions for a given angle. The transcript also introduces special right triangles and their ratios, and shows how to apply trigonometric functions to find missing angles or sides, emphasizing the use of a calculator for precise values.
Takeaways
- 📐 The expression 'sohcahtoa' is a mnemonic for the six trigonometric functions related to right triangles: sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), tangent (opposite/adjacent), cosecant (1/sine), secant (1/cosine), and cotangent (1/tan).
- 📐 In right triangle trigonometry, the three sides relative to an angle are the opposite, adjacent, and hypotenuse.
- 📐 The Pythagorean theorem (a^2 + b^2 = c^2) is fundamental in right triangles and helps find the missing side when two sides are known.
- 📐 Special right triangle ratios (3:4:5, 5:12:13, 8:15:17, 7:24:25) are useful for quickly finding the missing side or trigonometric values.
- 📐 To find the missing side or the values of trigonometric functions in a right triangle, one can apply the Pythagorean theorem and use the definitions of sine, cosine, and tangent.
- 📐 The reciprocal relationships between trigonometric functions (cosecant to sine, secant to cosine, cotangent to tangent) allow for easy derivation of one from the other.
- 📐 To solve for an unknown angle in a right triangle, one can use the inverse trigonometric functions (arc sine, arc cosine, arc tangent).
- 📐 The script provides examples of how to solve for missing sides and angles in right triangles using the concepts of trigonometry and the Pythagorean theorem.
- 📐 Trigonometry has practical applications in solving real-world problems such as angle of elevation and depression, and it's used in various fields like physics and engineering.
- 📚 The speaker also mentions a trigonometry course on Udemy, covering topics from basic concepts to more advanced applications and identities.
Q & A
What does the acronym SOHCAHTOA represent in trigonometry?
-SOHCAHTOA is a mnemonic used to remember the trigonometric functions for right triangles. It stands for Sine (opposite/hypotenuse), Cosine (adjacent/hypotenuse), and Tangent (opposite/adjacent).
What are the three sides of a right triangle?
-The three sides of a right triangle are the opposite side (to the angle), the adjacent side (next to the angle), and the hypotenuse (the side across the right angle).
How does the Pythagorean theorem relate to the sides of a right triangle?
-The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, it is represented as a^2 + b^2 = c^2, where c is the hypotenuse and a and b are the other two sides.
What are the reciprocal trigonometric functions based on SOHCAHTOA?
-The reciprocal trigonometric functions based on SOHCAHTOA are Cosecant (co) which is 1/Sine (sin), Secant (sec) which is 1/Cosine (cos), and Cotangent (cot) which is 1/Tangent (tan).
How can you find the missing side of a right triangle given two sides and an angle?
-To find the missing side of a right triangle, you can use the Pythagorean theorem (a^2 + b^2 = c^2) to solve for the unknown side (c). If the angle is given, you can use the trigonometric functions (sine, cosine, or tangent) to find the ratio of the known sides and then solve for the missing side.
What are some special right triangle ratios?
-Some special right triangle ratios are 3:4:5, 5:12:13, 8:15:17, and 7:24:25. These ratios can be scaled up to find the sides of larger right triangles, and they are useful for quickly solving problems without a calculator.
How do you calculate the value of sine, cosine, and tangent for a given angle in a right triangle?
-To calculate the values of sine, cosine, and tangent for a given angle, you use the ratios of the sides of the right triangle. Sine is the opposite side divided by the hypotenuse, cosine is the adjacent side divided by the hypotenuse, and tangent is the opposite side divided by the adjacent side.
What is the process for finding the missing angle in a right triangle with given side lengths?
-To find the missing angle in a right triangle, you first determine which side is missing based on the given side lengths and the known angle. Then, you use the inverse trigonometric function (arc sine for sine, arc cosine for cosine, or arc tangent for tangent) to find the angle. For example, if you have the opposite and adjacent sides, you'd use the arc tangent function.
How can you use the trigonometric functions to solve for an unknown side length in a right triangle?
-You can use the trigonometric functions to solve for an unknown side length by setting up an equation with the known side lengths and the trigonometric function that corresponds to the missing side. For example, if you have the adjacent and hypotenuse and need to find the opposite side, you'd use the cosine function and solve for the unknown side.
What is the significance of the trigonometry course mentioned in the script?
-The trigonometry course mentioned in the script is an online course available on Udemy that covers various topics in trigonometry, including angles, radians, the unit circle, right triangle trigonometry, trigonometric functions of any angle, graphing, inverse trig functions, and applications of trig functions. It is designed to help students understand and apply trigonometry concepts.
What are the steps to find the value of an unknown side length (x) given an angle (in degrees) and one side length in a right triangle?
-To find the value of an unknown side length (x), you first identify the trigonometric function associated with the given angle and side length. Then, you set up the equation using the known side length and the trigonometric function ratio. Finally, you solve for x by performing the necessary arithmetic operations, which may involve using a calculator for the trigonometric function values.
Outlines
📚 Introduction to Right Triangle Trigonometry
This paragraph introduces the concept of right triangle trigonometry, focusing on the SOHCAHTOA mnemonic. It explains the relationship between the angle (theta) and the three sides of the triangle: opposite (O), adjacent (A), and hypotenuse (H). The Pythagorean theorem is briefly mentioned, but the main emphasis is on the six trigonometric functions: sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot). The paragraph provides a method to find the missing side of a right triangle using the Pythagorean theorem and how to calculate the trigonometric functions given the values of two sides and an angle.
🔍 Solving Trigonometric Problems with Special Triangles
The second paragraph delves into solving trigonometric problems using special right triangles, such as the 3-4-5 and 5-12-13 triangles. It explains how to find the missing side and calculate the six trigonometric functions for a given triangle. The paragraph also introduces the concept of special triplets and how they can be used to quickly find the missing side of a triangle. It provides examples of how to use the SOHCAHTOA mnemonic to find the values of sine, cosine, and tangent, and their reciprocals, cosecant, secant, and cotangent.
📐 Applying Trigonometry to Find Missing Sides and Angles
This paragraph demonstrates how to apply trigonometry to find missing sides and angles in right triangles. It explains the process of using the tangent function to find the missing side given an angle and an adjacent side, and how to use the sine and cosine functions to find the hypotenuse and adjacent side when the opposite side and angle are known. The paragraph provides examples of calculating trigonometric functions for different angles and how to use them to solve for unknown sides and angles in right triangles.
🎓 Accessing the Trigonometry Course on Udemy
The fourth paragraph discusses the availability of a trigonometry course on Udemy, which covers various topics in trigonometry. It outlines the course content, including sections on angles, radians, the unit circle, right triangle trigonometry, trigonometric functions of any angle, graphing, inverse trig functions, and applications of trig functions. The paragraph provides instructions on how to access the course on Udemy and mentions that while two-thirds of the course is complete, additional sections are planned to be added in the future.
🤔 Additional Resources and Course Updates
The final paragraph provides additional information about the trigonometry course, including the topics that are still to be added such as the law of sines, law of cosines, polar coordinates, and other advanced topics. It encourages students to reach out with any questions and assures them that more content will be added to the course over time, emphasizing the comprehensive nature of the course and its ongoing development.
Mindmap
Keywords
💡sohcahtoa
💡right triangle trigonometry
💡Pythagorean theorem
💡trigonometric functions
💡sine
💡cosine
💡tangent
💡cosecant
💡secant
💡cotangent
💡special right triangles
Highlights
The expression 'sohcahtoa' is a mnemonic for remembering the trigonometric functions sine, cosine, tangent, cosecant, secant, and cotangent in relation to the sides of a right triangle.
In right triangle trigonometry, the sides are named opposite, adjacent, and hypotenuse with respect to the angle theta.
The Pythagorean theorem (a^2 + b^2 = c^2) applies to right triangles and is used to find the missing side of a triangle.
Special right triangle ratios include 3-4-5, 5-12-13, 8-15-17, and 7-24-25, which can be scaled for other right triangles.
To find the missing side of a right triangle, use the Pythagorean theorem and the known values of the other two sides.
The values of sine, cosine, and tangent for a right triangle can be calculated using the ratios of the sides with respect to the angle.
Cosecant, secant, and cotangent are the reciprocals of sine, cosine, and tangent, respectively.
The trigonometric functions sine, cosine, and tangent can be used to find the missing side of a right triangle given two sides and an angle.
The angle can be found using the inverse trigonometric functions (arc sine, arc cosine, arc tangent) when given the values of two sides in a right triangle.
The trigonometry course on Udemy covers topics such as angles, radians, the unit circle, right triangle trigonometry, and trigonometric functions of any angle.
The course also includes sections on graphing trigonometric functions, inverse trig functions, and applications of trig functions in problem-solving.
The mnemonic 'sohcahtoa' is essential for solving right triangle trigonometry problems and understanding the relationship between the angle and the sides of the triangle.
The lesson provides a method for finding the values of all six trigonometric functions for a given right triangle and angle.
By knowing the special right triangle ratios, one can quickly find the missing side and trigonometric values for various problems.
The process of finding the missing side or angle in a right triangle involves using the Pythagorean theorem and inverse trigonometric functions.
The course curriculum includes a variety of topics such as angle conversion, unit circle, trig functions, and trigonometric identities, providing a comprehensive understanding of trigonometry.
Transcripts
Browse More Related Video
Trigonometry

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)
Trigonometry - How To Solve Right Triangles
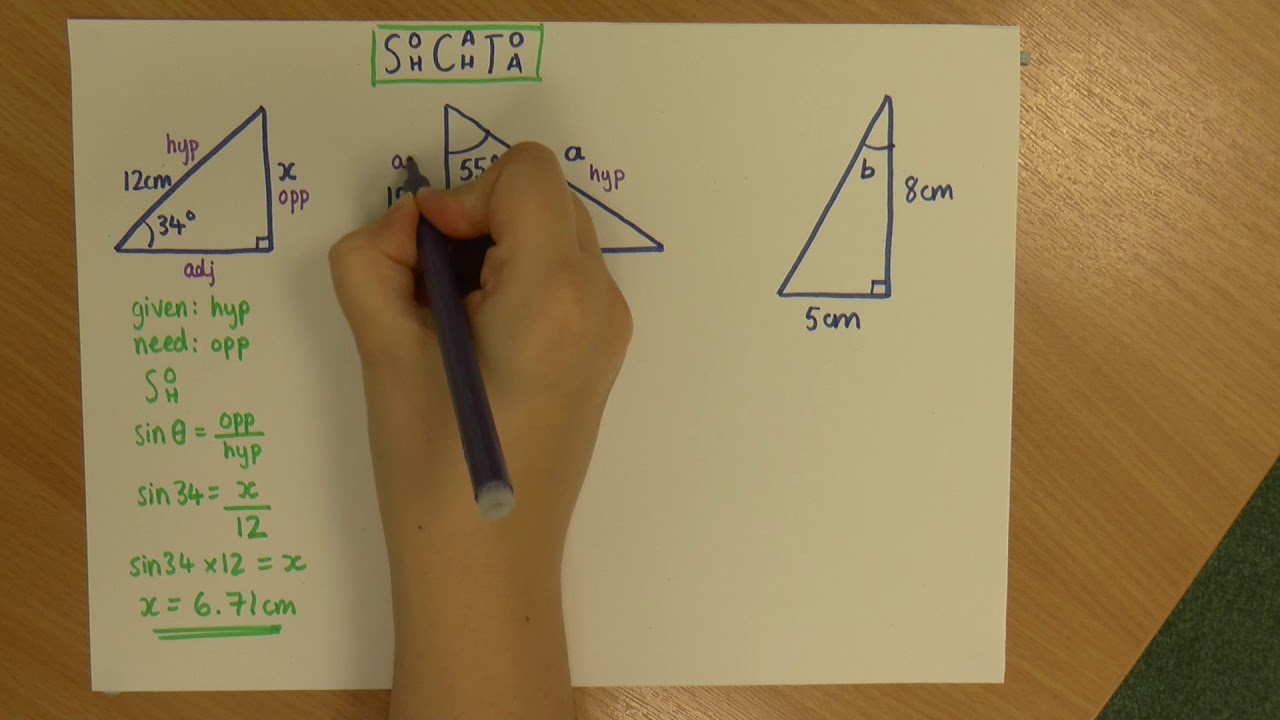
Trigonometry: Finding missing sides and angles
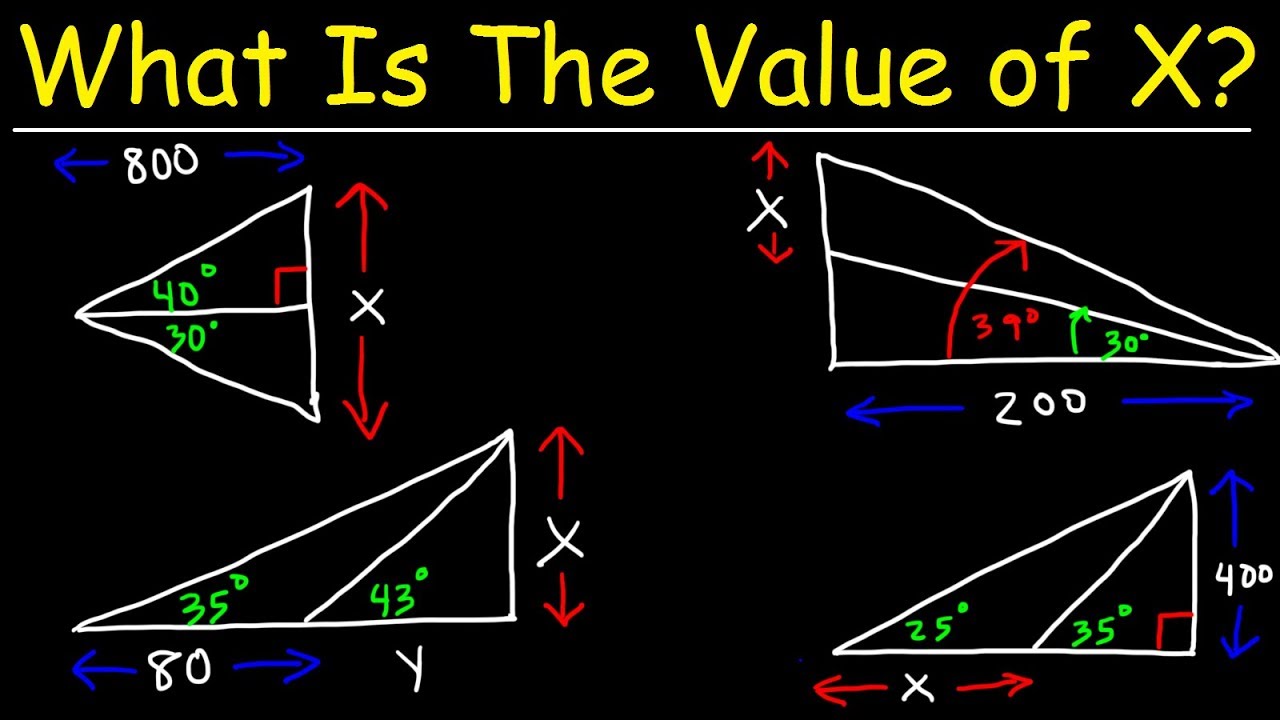
How To Solve Two Triangle Trigonometry Problems
5.0 / 5 (0 votes)
Thanks for rating: