AP Calculus AB: Lesson 7.4: Disk and Washer Method
TLDRThis lesson delves into calculating the volume of solids formed by revolving a region around an axis using definite integrals. It introduces the disk method for regions revolving around the x-axis and the washer method for regions with a hole in the middle. Through examples, the instructor demonstrates setting up integrals for both methods, emphasizing the importance of drawing reference rectangles perpendicular to the axis of rotation. The video guides viewers through various problems, highlighting the process of finding volumes of solids created by rotating specific functions around different lines, and concludes with a critical thinking question comparing the two methods.
Takeaways
- 📚 The lesson focuses on calculating the volume of a solid of revolution using definite integrals with the disk method and the washer method.
- 🔄 The disk method involves revolving a region around the x-axis, creating a solid figure, and calculating its volume by summing the volumes of infinitesimally thin disks.
- 🔧 The formula for the volume of a single disk is derived from the volume of a cylinder, using the area of the circular face (pi * radius^2) multiplied by the height (dx).
- 📏 The radius of the disk is determined by the vertical distance between the function f(x) and the x-axis, and the height is the width of the subinterval (dx).
- ∫ The volume of the entire solid is found by integrating the volume of a single disk over the interval [a, b], leading to the formula ∫[a, b] pi * f(x)^2 * dx.
- 🌀 An example is provided to find the volume of a solid obtained by rotating the region bounded by y = sqrt(2x), y = 0, and x = 1 around the x-axis, resulting in a volume of pi.
- 🛠 The washer method is introduced for cases where there is an empty space between the region and the axis of rotation, creating a disk with a hole (washer).
- 🔗 The relationship between the disk and washer methods is that the washer method is essentially a disk method with an additional step of subtracting the volume of the inner disk (hole) from the outer disk.
- 📐 The setup for the washer method involves finding the outer and inner radius functions, R(x) and r(x), and integrating [R(x)^2 - r(x)^2] over the interval.
- 📈 Several examples illustrate the application of the washer method for different regions and lines of rotation, emphasizing the importance of correctly setting up the integral.
- 🤔 The critical thinking question posed is how the disk method and washer method are related and when to use each, highlighting the need for understanding the context of each method's application.
Q & A
What are the two methods discussed in the script for calculating the volume of a solid of revolution?
-The two methods discussed in the script are the disk method and the washer method.
What is the basic principle behind the disk method for calculating volume?
-The disk method calculates the volume of a solid of revolution by considering the volume of infinitesimally thin disks created by rotating a region around an axis. The volume of each disk is found by multiplying the area of the circular face (pi times the radius squared) by the height (dx), and then integrating over the interval of rotation.
How does the washer method differ from the disk method?
-The washer method is used when there is an empty space between the region being rotated and the axis of rotation. It involves calculating the volume of an outer 'disk' and subtracting the volume of an inner 'disk', which accounts for the empty space, resulting in a 'washer' shape.
What is the formula for the volume of a solid using the disk method with a vertical slice?
-The formula for the volume of a solid using the disk method with a vertical slice is given by the definite integral from 'a' to 'b' of pi times the function f(x) squared, dx.
What is the significance of the reference rectangle in setting up the disk and washer methods?
-The reference rectangle is crucial in setting up the disk and washer methods as it helps to visualize the cross-section of the solid and determine the radius of the disks being integrated. It must always be drawn perpendicular to the axis of rotation.
How do you determine the interval for the integral when using the disk method?
-The interval for the integral is determined by the limits of the region being rotated. It starts at 'a', the x-coordinate of the left endpoint of the region, and ends at 'b', the x-coordinate of the right endpoint.
Can you provide an example of a solid obtained by rotating a region around the x-axis and its volume calculation?
-An example given in the script is the rotation of the region bounded by y = sqrt(2x), y = 0, and x = 1 around the x-axis. The volume is calculated using the disk method with the integral of pi times (sqrt(2x))^2 dx from 0 to 1, resulting in a volume of pi.
What is the key difference between the washer method and the disk method in terms of the solid's shape?
-The key difference is that the washer method accounts for a solid with an empty space in the middle (a hole), creating a washer shape, whereas the disk method is used for solid shapes without any empty space.
How do you set up the washer method for a region rotated around the y-axis?
-For a region rotated around the y-axis using the washer method, you would calculate the horizontal distance from the axis of rotation to the outer and inner functions, square these distances to get the radii, and then set up an integral from 'c' to 'd' of pi times the outer radius squared minus the inner radius squared, dy.
What is the formula for the volume of a solid using the washer method with a vertical slice?
-The formula for the volume of a solid using the washer method with a vertical slice is the definite integral from 'a' to 'b' of pi times the outer radius function squared minus the inner radius function squared, dx.
Outlines
📚 Introduction to Calculating Solid of Revolution Volumes
This paragraph introduces the topic of calculating the volume of solids created by revolving a region around an axis using definite integrals. The focus is on two methods: the disk method and the washer method. The disk method involves finding the volume of a solid obtained by rotating a region around the x-axis, starting with a simple rectangle and considering its transformation into a circular disc when rotated. Key terms and the foundational concept of revolving a region to form a solid figure are explained, setting the stage for deeper exploration in subsequent paragraphs.
🔍 Developing the Disk Method Formula
The paragraph delves into the specifics of the disk method, explaining how to calculate the volume of a single disk formed by rotating a rectangle around the x-axis. It discusses the transformation of a rectangle into a cylinder and the subsequent calculation of its volume using the area of the circular face and the height of the cylinder. The formula for the volume of a disk is derived, involving the function defining the top surface of the rectangle and the width of the subintervals on the x-axis, leading to an expression involving pi, the square of the function value, and the change in x.
🌀 Summing Disk Volumes for Complete Solid
This section discusses the transition from calculating the volume of a single disk to the entire solid formed by adding an infinite number of these disks. It explains how to use an integral to sum the volumes of all disks as the width of each subinterval approaches zero. The process involves setting up a definite integral from the bounds of the region, using the derived formula for a single disk's volume and considering the infinite nature of the sum, which is represented by the integral.
📉 Example: Volume of a Solid by Rotating a Region
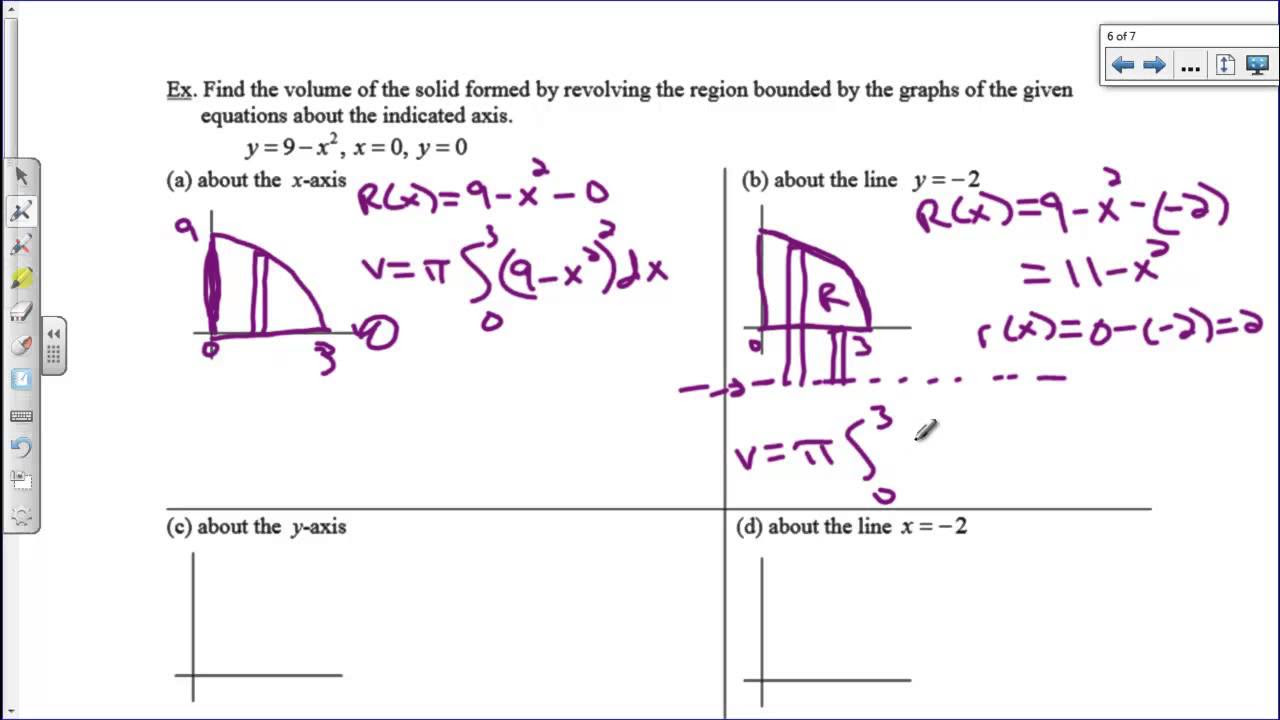
The paragraph presents a practical example of using the disk method to find the volume of a solid obtained by rotating a specific region around the x-axis. The region is bounded by a curve and two vertical lines, and the paragraph guides through determining the interval for the integral, setting up the reference rectangle, and applying the disk method formula to find the volume. It also includes a step-by-step calculation, leading to the final volume of the solid.
📐 Sketching the Solid and Reviewing Disk Method Formula
This paragraph emphasizes the importance of sketching the solid for a better understanding and then reviews the formula for the disk method when using a vertical slice. It explains the process of reflecting the region across the axis of rotation to visualize the solid and provides a formula for calculating the volume when the region is revolved around the x-axis, using the radius and height obtained from the function and the limits of integration.
🔄 Setting Up the Washer Method
The paragraph introduces the washer method, which is used when there's an empty space between the region and the axis of rotation. It explains the concept of a washer, which is like a disk with a hole in the middle, and the strategy of finding the volume of the empty space to then subtract it from the volume of a solid disk. The paragraph sets up the integral for the washer method, considering both the outer and inner radii and their respective volumes.
📐 Applying the Washer Method to a Specific Problem
This section applies the washer method to a problem involving the rotation of a region bounded by two functions around the x-axis. It explains how to find the volume of the outer and inner solids separately and then subtract them to get the volume of the washer. The paragraph includes a step-by-step guide on setting up the integrals for both the outer and inner functions and combining them into a single integral to find the final volume.
🔄 General Formula for Washer Method and Problem Setup
The paragraph presents the general formula for the washer method when using a vertical slice and explains the importance of drawing reference rectangles perpendicular to the axis of rotation. It walks through the process of setting up a problem for the washer method, including determining the interval and the expressions for the outer and inner radii, and emphasizes the importance of correctly setting up the integral for accurate volume calculation.
📉 Calculating Volume with Washer Method: Horizontal Slice
This section discusses the washer method when using a horizontal slice, explaining the difference in setup when the axis of rotation requires horizontal rectangles. It provides a detailed example of setting up and calculating the volume of a solid formed by revolving a region around a horizontal line, including determining the correct expressions for the outer and inner radii and integrating to find the volume.
📐 Final Thoughts on Disk and Washer Methods
The final paragraph wraps up the lesson by highlighting the importance of correctly setting up the disk and washer methods, emphasizing the need to draw reference rectangles perpendicular to the axis of rotation. It also poses a critical thinking question about the relationship between the disk and washer methods and the circumstances under which each should be used, encouraging viewers to reflect on the content covered.
Mindmap
Keywords
💡Solid of Revolution
💡Disk Method
💡Washer Method
💡Definite Integrals
💡Cylinder
💡Riemann Sums
💡Axis of Rotation
💡Volume Calculation
💡Graph
💡Function
Highlights
Introduction to calculating the volume of a solid of revolution using definite integrals with the disk method and washer method.
Explanation of the disk method formula for finding the volume of a solid obtained by rotating a region around the x-axis.
Development of a formula for the disk method by considering the volume of a single disk created by rotating a rectangle.
Illustration of the transformation of a rectangle into a circular disc when rotated around the x-axis.
Calculation of the volume of a cylinder using the area of its circular face and its height.
Use of definite integrals to sum the volumes of infinitely many disks to find the total volume of the solid.
Example problem demonstrating the calculation of the volume of a solid formed by rotating the region bounded by a specific function around the x-axis.
Strategy for setting up integrals for solids of revolution, including determining the interval and the function's behavior.
Application of the disk method to a region rotated around the y-axis, using horizontal cross-sections.
Introduction of the washer method for calculating the volume of a solid with an empty space between the region and the axis of rotation.
Explanation of the difference between the disk method and washer method, and the conditions for their usage.
Demonstration of the washer method with an example problem involving rotation around a vertical line.
Critical thinking question posed about the relationship between the disk method and washer method, and their respective use cases.
Teaser for the next lesson, which will cover the shell method or method of cylindrical shells for finding the volume of a solid of revolution.
Emphasis on the importance of drawing reference rectangles perpendicular to the axis of rotation when setting up problems.
Encouragement for viewers to practice problem setup and integral computation to master the disk and washer methods.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: