Disc/Washer Method vs. Shell Method (rotated about different lines)

blackpenredpen

27 Apr 202038:22

EducationalLearning

32 Likes 10 Comments

TLDRThis transcript outlines a comprehensive exploration of calculus, specifically focusing on finding the area and volume of regions bounded by curves. The video demonstrates both the vertical and horizontal rectangle approaches to calculate the area under the curves y=√x and y=1/2x, and then extends the discussion to include the volume of the resulting solids when these regions are rotated around different axes. The presenter covers the disk method and the shell method for calculating volumes, emphasizing the importance of correctly identifying the radius and height for each method. The video also addresses the challenges of integrating when there's a hole in the middle of the solid, referring to it as the 'washer method.' Throughout the explanation, the presenter provides step-by-step instructions and mathematical equations, making the complex process of calculating areas and volumes more accessible.

Takeaways

📐 **Understanding the Problem**: The script begins by setting up a mathematical problem involving finding the area of a region bounded by two functions, y = √x and y = 1/2x, and then rotating this region around an axis to find the volume.
📈 **Vertical and Horizontal Rectangles**: Two methods for finding the area are discussed: the vertical rectangle method, which involves calculating the area of thin vertical rectangles, and the horizontal rectangle method, which uses horizontal slices.
🔢 **Integration for Area Calculation**: The process of integrating the difference between the top function (√x) and the bottom function (1/2x) over the interval [0, 4] is used to find the area of the region.
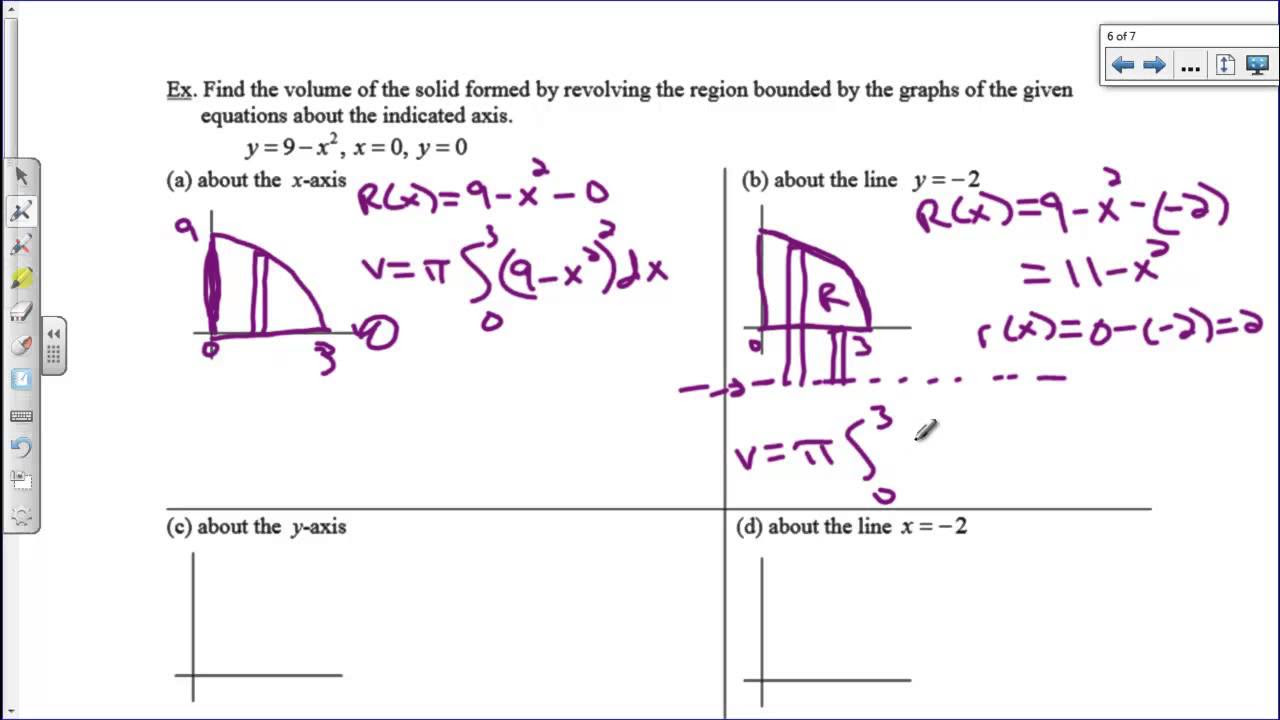
🔴 **Disk Method for Volume**: The volume of the solid generated by rotating the region around the x-axis is found using the disk method, which involves integrating the area of thin disks over the interval.
⭕ **Washer Method for Volume**: An alternative to the disk method is the washer method, which is used when there is a hole in the middle of the solid. This method is also demonstrated for the same region rotated around the x-axis.
📐 **Shell Method for Volume**: The shell method is introduced as another technique for calculating volume, where the solid is thought of as a collection of cylindrical shells. This method is particularly useful when dealing with solids with holes or complex shapes.
🤔 **Choosing the Right Method**: The script emphasizes the importance of choosing the appropriate method (disk, washer, or shell) based on the geometry of the region and the axis of rotation.
🧮 **Labeling and Setting Up the Integral**: A key step in both the disk and shell methods is correctly labeling the radius and height of the slices or shells and setting up the integral that represents the volume.
🔁 **Practice and Breakdown**: The importance of practicing different methods and breaking down the problem into manageable parts is highlighted to ensure a solid understanding of the concepts.
📉 **Subtracting for Inner Regions**: When the solid has an inner region (as in the washer method), the volume of this inner region is subtracted from the volume of the outer region to find the final volume.
📚 **Applying the Methods to Various Scenarios**: The script walks through applying the disk, washer, and shell methods to different scenarios, including rotations around both the x-axis and y-axis, and regions defined by various functions.

Q & A

What is the first step in finding the area of a region bounded by two curves using vertical rectangles?
-The first step is to draw a vertical rectangle and label the base and height. The base is a small change in the x-direction, labeled as dx, and the height is the difference between the y-values of the top and bottom functions, which are the curves defining the region.
How do you find the x-values where the two curves intersect?
-To find the x-values where the two curves intersect, set the two equations equal to each other, solve for x, and determine the range over which to integrate.
What is the formula for the volume of a solid of revolution when using the disk method?
-The formula for the volume of a solid of revolution using the disk method is V = π * ∫[R(y)^2] * dy, where R(y) is the radius function in terms of y, and the integral is evaluated over the range of y-values from the lower to the upper limit of the region.
How is the washer method different from the disk method in calculating the volume of a solid of revolution?
-The washer method involves subtracting the volume of a smaller disk (with a hole in the middle) from the volume of a larger disk. It is used when the region to be revolved has a hole in it. The disk method, on the other hand, does not involve such a subtraction and is used for solid regions without a hole.
What is the shell method and how is it applied when calculating the volume of a solid of revolution?
-The shell method involves considering the solid as being made up of infinitesimally thin cylindrical shells. The volume is calculated by integrating the product of the circumference of the shell (2π times the radius), the height (the difference in x-values or y-values depending on the axis of rotation), and the thickness (dx or dy) over the range of the region.
When is the shell method preferable over the disk or washer method?
-The shell method is preferable when the solid of revolution has a hole in the middle, as it simplifies the calculation by considering the cylindrical shells that make up the solid.
How do you determine the radius and height for the shell method?
-For the shell method, the radius is determined by the distance from the axis of rotation to the outer edge of the shell, which may require algebraic manipulation based on the given equations. The height is the difference in the x-values (or y-values) between the inner and outer edges of the shell.
What is the purpose of sketching a 3D picture when calculating the volume of a solid of revolution?
-Sketching a 3D picture helps visualize the solid and understand the geometry of the problem, which aids in correctly identifying the radius and height for the disk or shell method calculations.
How do you find the volume of a solid of revolution when the region is rotated about an axis that is not the x or y-axis?
-When the region is rotated about an axis that is not the x or y-axis, you would first need to determine the new radius and height in terms of the variables associated with the axis of rotation. Then, you would use the appropriate method (disk, washer, or shell) to calculate the volume, integrating over the correct range.
What is the significance of the thickness (dx or dy) in the disk and shell methods?
-The thickness (dx or dy) represents an infinitesimally small slice of the solid in the disk or shell method. It is a crucial component in the integral that calculates the volume of the solid of revolution.
How does the choice of the axis of rotation affect the calculation of the volume of a solid of revolution?
-The choice of the axis of rotation affects the shape of the resulting solid and, consequently, the method and equations used for the calculation. For example, rotating around the x-axis or y-axis may lead to different radius and height functions, and thus different integrals for the volume calculation.

Outlines

00:00

📐 Introduction to Area and Volume Calculations

The video begins with an introduction to finding the area of a region bounded by two functions, y = √x and y = 1/2x. The presenter explains the concept of vertical rectangles for integration and how to find the limits of integration by setting the functions equal to each other and solving for x. The limits are found to be from x = 0 to x = 4. The presenter also mentions the possibility of using a horizontal rectangle approach.

05:00

🔍 Calculating Area with Horizontal Rectangles

The presenter continues with the horizontal rectangle method, explaining how to label the base and height of the rectangle in terms of dy and dx. The area under consideration is expressed in terms of y, and the integration is performed from y = 0 to y = 2. The process is demonstrated for both the region itself and after rotation around the x-axis to find the volume using the disk method, emphasizing the importance of considering the outer and inner parts of the rotated region.

10:03

📏 Shell Method for Volume Calculation

The video introduces the shell method for finding the volume of the region rotated around the x-axis. The presenter illustrates how to visualize the shell by considering a vertical rectangle and its mirror image. The volume is calculated by integrating the product of 2π times the radius (which changes with y), the height (the difference between the outer and inner functions of y), and the thickness dy, from y = 0 to y = 2. The method is particularly useful when there is a hole in the middle of the solid.

15:04

🌀 Rotation Around X=5 Axis

The presenter discusses rotating the region around the x-axis at x = 5. The focus is on the disk method, where the thickness is dy, and the radius is calculated based on the x-values relative to the axis of rotation. The radius is expressed as 5 - x, and the volume is found by integrating pi times the radius squared, times the thickness dy, from y = 0 to y = 2. The process is detailed, emphasizing the setup and calculation steps.

20:05

🧮 Shell Method Application Around X=5 Axis

The video demonstrates the shell method for the same region rotated around x = 5. The presenter explains how to draw a vertical shell and calculate the radius and height for the shell method. The radius is the distance from the axis of rotation to the outer curve, which is 5 - x, and the height is the difference between the y-values of the curves. The volume is then found by integrating 2pi times the radius times the height times the thickness dx, from x = 0 to x = 4.

25:07

🏗️ Volume Calculation for Y=3 Rotation

The presenter shifts the focus to rotating the region around y = 3, using both the washer and shell methods. For the washer method, the radius is determined by the distance from the axis of rotation to the curve, and the height is the difference between the y-values of the curves. The volume is calculated by integrating pi times the radius squared times the thickness dx from x = 0 to x = 4. The shell method is also demonstrated, with the radius being 3 - y and the height calculated based on the x-values of the curves.

30:10

📝 Final Thoughts on Shell and Washer Methods

The video concludes with a summary of the shell and washer methods for calculating volumes of solids of revolution. The presenter emphasizes the importance of understanding the setup for each method, particularly when dealing with axes of rotation that are not the standard x or y axes. The presenter encourages practice and reiteration of the methods to solidify understanding and prepare for exams.

Mindmap

Keywords

💡Area Calculation

Area Calculation refers to the process of determining the size of a two-dimensional region bounded by curves. In the video, it is a central theme as the speaker demonstrates how to find the area of a region bounded by the functions y = square root of x and y = 1/2 x. The method involves using vertical or horizontal rectangles to approximate the region's area, which is then found by integrating the difference in the functions over a given interval.

💡Volume of Revolution

Volume of Revolution is the term used to describe the volume of a solid object created by rotating a two-dimensional region around an axis. In the video, the speaker explains how to find the volume of a region when it is rotated around the x-axis and y-axis using both the washer and shell methods. This is a key concept as it demonstrates how to apply calculus to find the volume of complex shapes.

💡Disk Method

The Disk Method is a technique used to calculate the volume of a solid of revolution by considering it as a collection of infinitesimally thin disks. The speaker uses this method to find the volume of the region rotated around an axis, by integrating the area of each disk (PI * R^2 * thickness) over the interval. It is illustrated in the video by drawing a thin disk and showing how it sweeps out a volume when rotated.

💡Shell Method

The Shell Method is another technique for finding the volume of a solid of revolution, where the solid is considered as a series of infinitesimally thin cylindrical shells. The video explains this method by drawing a vertical rectangle (shell) and showing that its volume can be calculated by integrating the product of the circumference of the shell (2 * PI * R), the height (difference in x-values), and the thickness (dy) over the interval.

💡Washer Method

The Washer Method is a specific application of the Disk Method used when the solid of revolution has a hole through its center. The video demonstrates this method by showing how to subtract the volume of the inner disk (hole) from the volume of the outer disk to find the volume of the annular shape. This method is particularly relevant when the region to be rotated has a hole, such as when the radius of the inner disk is given by a different function.

💡Integration

Integration is a fundamental concept in calculus that involves finding the accumulated value of a function over an interval, which in this context is used to calculate areas and volumes. The video uses integration to sum up the infinitesimally small areas of rectangles or disks that make up the region of interest. It is the mathematical process that allows the transition from the sum of rectangles to the area under a curve and from the sum of disks to the volume of a solid of revolution.

💡Solid of Revolution

A Solid of Revolution is the three-dimensional object created by rotating a two-dimensional region around an axis. The video script discusses finding the volume of various solids of revolution, which is a practical application of calculus in determining the space occupied by objects generated from rotational symmetry.

💡Rectangular Coordinates

Rectangular Coordinates, also known as Cartesian Coordinates, is a system of defining points in a plane through two perpendicular distances, one from the x-axis and one from the y-axis. In the video, the speaker uses rectangular coordinates to label the points where the curves intersect and to set up the integrals for calculating areas and volumes.

💡Curve Intersections

Curve Intersections refer to the points where two or more curves on a graph meet. The video discusses finding the points of intersection between y = square root of x and y = 1/2 x, which are necessary to determine the limits of integration when calculating the area and volume of the resulting regions.

💡Vertical and Horizontal Rectangles

Vertical and Horizontal Rectangles are the geometric shapes used in the approximation process of the area under a curve in the Disk and Washer methods. The video explains that for a vertical rectangle, the area is calculated using the width (dx) and the difference in the y-values (top function minus bottom function), while for a horizontal rectangle in the Shell method, the area is calculated using the height (dy) and the difference in the x-values.

💡Cylindrical Shells and Disks

Cylindrical Shells and Disks are the geometric representations used in the Shell and Disk methods, respectively. In the video, the speaker describes how to visualize these shapes when a region is rotated around an axis to form a solid of revolution. The cylindrical shell is an infinitesimally thin 'shell' wrapped around the curve, and the disk is an infinitesimally thin slice perpendicular to the axis of rotation.

Highlights

Introduction to finding the area of a region bounded by two functions using vertical and horizontal rectangles.

Explanation of the setup for vertical and horizontal rectangle approaches in integration.

Demonstration of how to calculate the area under the curve y=√x and y=1/2x using the given methods.

Use of the disk method to find the volume of the solid generated by rotating the region about the x-axis.

Illustration of the washer method, which accounts for a hole in the middle of the solid of revolution.

Application of the shell method to find the volume, which is particularly useful when there's a hole in the solid.

Process of rotating the region about the y-axis and the corresponding changes in the disk and shell methods.

Technique to calculate the volume when rotating about a vertical line, such as x=5, using the disk method.

Adjustments needed in the shell method when the axis of rotation is a vertical line other than the y-axis.

How to handle gaps in the region when applying the disk and shell methods for volumes of revolution.

Practical application of the disk and shell methods to calculate the volume of more complex regions.

Explanation of the importance of correctly identifying the radius and height in the shell method.

Approach to subtracting volumes when there are multiple disjoint regions in the solid of revolution.

Use of the disk method to find the volume when rotating about a horizontal line, such as y=3.

Conversion of the region's equations into the correct form for the shell method when rotating about a horizontal line.

Final walkthrough of the shell method for the volume of a solid generated by rotating a region about y=3.

Emphasis on practicing the problems first before referring to the solutions or handouts.

Transcripts

Browse More Related Video

Calculus 1 Lecture 5.2: Volume of Solids By Disks and Washers Method

Volume with Washers

Volume The Disc Method

Calculus AB Homework 7.5 Shell Method

AP Calculus AB: Lesson 7.5: Shell Method

Calculating volume by known cross sections

Related Tags

Mathematics Integration Disk Method Shell Method Volume Calculation Area Calculation Geometry Analytical Approach Educational Content Math Tutorial