Radians and Degrees

The Organic Chemistry Tutor

17 Jun 201718:54

EducationalLearning

32 Likes 10 Comments

TLDRThis transcript explains the concepts of angles measured in degrees and radians, highlighting the importance of understanding both systems. It defines a radian as the angle formed when the arc length of a circle is equal to its radius. The video teaches how to calculate angles in radians given arc length and radius, and how to convert between degrees and radians using the conversion factor π. It also covers common angles in radians and their positions on the unit circle, aiding in the understanding of trigonometry.

Takeaways

📏 Angles can be measured in degrees or radians, with radians being the central angle of a circle where the arc length equals the radius.
🔵 The symbol for radians is the absence of a degree symbol (°), so a number without a circle represents radians.
🤔 To define a radian: an angle with an arc length equal to the radius of the circle measures 1 radian.
📐 The formula to find the angle in radians is θ = s/r, where θ is the angle, s is the arc length, and r is the radius.
🔄 One full revolution of a circle is 360 degrees or 2π radians.
🌀 To convert degrees to radians, multiply the degree measure by π/180.
🔄 To convert radians to degrees, multiply the radian measure by 180/π.
📊 Common radian values and their corresponding locations are π/4 (45°), 3π/4 (135°), 5π/4 (225°), 7π/4 (315°), π/3 (60°), 2π/3 (120°), 4π/3 (240°), and 5π/3 (300°).
📐 To graph angles in standard position, convert radians to degrees to find the appropriate quadrant.
📚 The video script also mentions a comprehensive online trigonometry course available on Udemy, covering a variety of topics from basic concepts to more advanced trigonometry problems.
📍 Remembering the positions of common angles in radians is crucial for solving problems and understanding the unit circle.

Q & A

How are angles typically measured?
-Angles can be measured in either degrees or radians. Degrees are indicated with a small circle on top of the angle, while radians do not have this symbol.
What is the definition of a radian?
-A radian is the measure of the central angle of a circle such that the arc length of the circle is equal to the radius of the circle.
How can you calculate the angle in radians given the arc length and radius?
-To find the angle in radians, divide the arc length (s) by the radius (r). The result will give you the angle in radians.
How many radians are in a full circle?
-A full circle, or one full revolution, is equal to 2π radians.
What is the conversion factor from degrees to radians?
-The conversion factor from degrees to radians is π radians per 180 degrees.
How do you convert 60 degrees to radians?
-To convert 60 degrees to radians, multiply the degree measure by π/180, which simplifies to π/3 radians.
What is the process for converting negative angles from degrees to radians?
-To convert negative angles from degrees to radians, multiply the negative degree measure by π/180, and simplify the result to get the radian measure.
How do you convert radians into degrees?
-To convert radians into degrees, multiply the radian measure by 180/π, and simplify the expression to get the degree measure.
What are some common angles in radians and their corresponding locations on the unit circle?
-Common angles in radians include π/4 (45 degrees), 3π/4 (135 degrees), 5π/4 (225 degrees), 7π/4 (315 degrees), π/3 (60 degrees), 2π/3 (120 degrees), π/6 (30 degrees), 5π/6 (150 degrees), and 7π/6 (210 degrees).
How can you graph an angle of π/4 radians in standard position?
-To graph π/4 radians in standard position, first convert it to degrees, which is 45 degrees. Then, draw the angle on the unit circle between the 0 and 90-degree marks.
What are the angles on the x and y axis in radians?
-The angles on the x and y axis in radians are 0 (0 degrees), π/2 (90 degrees), π (180 degrees), 3π/2 (270 degrees), and 2π (360 degrees).

Outlines

00:00

📏 Understanding Degrees and Radians

This paragraph introduces the concepts of measuring angles in degrees and radians. It explains the visual cue of a circle with a dot to indicate degrees and the absence of the circle for radians. The definition of a radian is provided as the central angle of a circle where the arc length is equal to the radius. The process of calculating the angle in radians by dividing the arc length (s) by the radius (r) is detailed, along with examples to illustrate the concept.

05:00

🔄 Converting Between Degrees and Radians

This section focuses on the conversion between degrees and radians. It presents the conversion factor where 180 degrees is equal to pi radians. The method for converting angles from degrees to radians by multiplying the degree measure by pi/180 is explained with examples. Conversely, the process for converting radians to degrees by multiplying the radian measure by 180/pi is also discussed, with additional examples provided for clarity.

10:02

📐 Graphing Angles in Standard Position

The paragraph discusses the process of graphing angles in standard position when given in radians. It suggests the utility of converting radians to degrees for easier graphing and provides a step-by-step guide on how to plot angles like pi/4 and 7pi/6. The paragraph also lists common angles in radians with their corresponding quadrants and degrees, emphasizing the importance of memorizing these for quick reference in trigonometry.

15:05

🎓 Common Radian Values and Their Locations

This part of the script focuses on the memorization of common radian values and their locations on the unit circle. It provides a method for remembering these values by relating them to multiples of 45 and 60 degrees. The paragraph lists angles such as pi/4, 3pi/4, 5pi/4, 7pi/4, pi/3, 2pi/3, 4pi/3, and 5pi/3, along with their corresponding degrees and quadrants. The importance of knowing these angles for trigonometry is emphasized, and additional angles on the x and y axis are mentioned, including 0, pi/2, and 3pi/2 radians.

Mindmap

Keywords

💡angle

An angle is a measure of rotation or the figure formed by two rays, called sides, sharing a common endpoint, called the vertex. In the context of the video, angles can be measured in degrees or radians, which are two different units of angular measurement. The video emphasizes the importance of understanding both systems, especially when dealing with trigonometry and the unit circle.

💡radians

A radian is a unit of angular measurement that represents the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. It is used in many areas of mathematics, especially in calculus and trigonometry. The video explains that radians are used when there is no circle symbol (°) next to the angle measure.

💡degrees

A degree is another unit of angular measurement, where a full circle is divided into 360 equal parts. Each part represents one degree. Degrees are commonly used in everyday language and are the standard unit of angle measurement in many fields, including geometry and navigation. The video contrasts degrees with radians and explains how to convert between the two.

💡conversion

Conversion in the context of the video refers to the process of changing an angle's measurement from one unit (degrees or radians) to another. This is a crucial skill in trigonometry and mathematics, as it allows for the calculation and comparison of angles measured in different systems.

💡arc length

Arc length is the distance around the circumference of a circle between two points. In the context of radians, it is the length of the arc that corresponds to a specific angle. The video explains that a radian is defined as the angle subtended by an arc length equal to the radius of the circle.

💡unit circle

A unit circle is a circle with a radius of 1 and is used as a standard reference in trigonometry for defining trigonometric functions. The video mentions the unit circle in relation to evaluating trigonometric functions and understanding common angles in radians.

💡trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. It is used to solve problems involving lengths, angles, and areas of triangles and other geometric figures. The video is focused on teaching various concepts and techniques in trigonometry, including angle measurement and conversion.

💡standard position

In trigonometry, a standard position refers to the placement of an angle on a coordinate plane with its vertex at the origin and its initial side along the positive x-axis. The video explains how to graph angles in standard positions when they are given in radians.

💡common angles

Common angles are specific angles that frequently appear in trigonometry problems and have well-known values in both degrees and radians. These angles have special significance and are often used as reference points in trigonometric calculations.

💡online trigonometry course

The online trigonometry course mentioned in the video is a comprehensive educational resource available on Udemy that covers a wide range of topics in trigonometry, from basic concepts to more advanced topics like solving word problems and verifying trigonometric identities.

Highlights

Angles can be measured in degrees or radians.

A circle with a small circle on top indicates degrees, without it indicates radians.

Definition of a radian: the central angle of a circle where the arc length is equal to the radius.

To find the angle in radians, divide the arc length (s) by the radius (r).

One full revolution of a circle is 360 degrees or 2π radians.

Conversion factor from degrees to radians: multiply by π/180.

To convert from radians to degrees, multiply by 180/π.

Negative angles in degrees can be converted to negative angles in radians.

Common angles in radians and their locations: π/4, 3π/4, 5π/4, and 7π/4.

Angles in radians that are easy to remember: π/3, 2π/3, 4π/3, and 5π/3.

Angles on the x and y axis: 0° (0 radians), π/2 (90°), π (180°), and 3π/2 (270°).

To graph angles in standard position, convert radians to degrees if necessary.

Angles like π/6, 5π/6, and 7π/6 can be graphed by converting to degrees (30°, 150°, 210°).

The radius can be thought of as the length per unit radian, which helps in understanding the unit cancellation.

Examples provided for converting specific angles like 60°, 150°, -225°, and -30° to radians.

Detailed explanation of converting negative angles like -30° and -225° to radians.

Online trigonometry course mentioned for further learning and practice.

Transcripts

Browse More Related Video

Introduction to Trigonometry: Angles and Radians

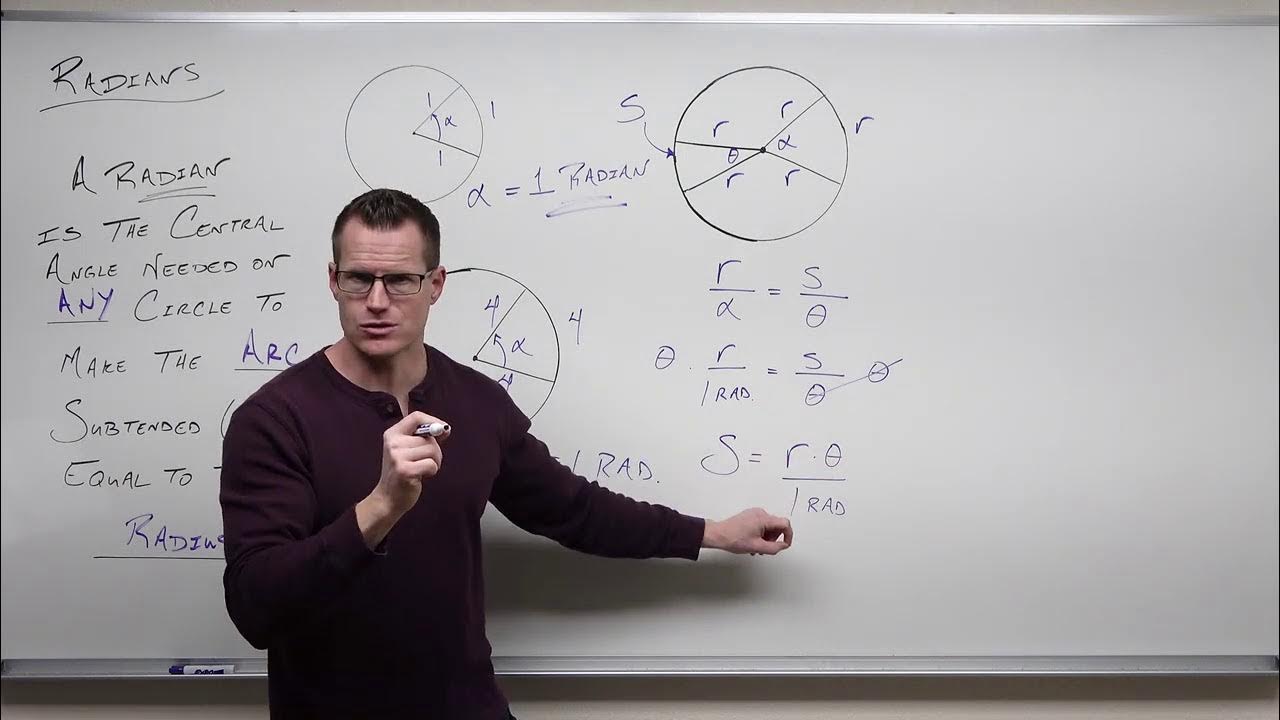
Introduction to Radians (Precalculus - Trigonometry 3)

CONVERTING DEGREE MEASURE TO RADIAN MEASURE AND VICE VERSA || PRE-CALCULUS

Converting Radians and Degrees (Precalculus - Trigonometry 4)

Arc Length of a Circle Formula - Sector Area, Examples, Radians, In Terms of Pi, Trigonometry

Trig 0.1 - Angles, Degrees and Radians

Radians and Degrees

Takeaways

Q & A

How are angles typically measured?

What is the definition of a radian?

How can you calculate the angle in radians given the arc length and radius?

How many radians are in a full circle?

What is the conversion factor from degrees to radians?

How do you convert 60 degrees to radians?

What is the process for converting negative angles from degrees to radians?

How do you convert radians into degrees?

What are some common angles in radians and their corresponding locations on the unit circle?

How can you graph an angle of π/4 radians in standard position?

What are the angles on the x and y axis in radians?