How to evaluate for the composition of two trigonometric functions

Brian McLogan

9 Dec 201507:09

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses the common misconception that the cosine inverse function cancels out the cosine function, especially in trigonometric compositions. It emphasizes the importance of understanding the order of operations and the restrictions on the domain of cosine to correctly solve problems. The example provided illustrates how to determine the correct angle when multiple angles produce the same cosine value by considering the quadrant in which the angle lies and the restrictions on the domain of the cosine inverse function.

Takeaways

🔍 The misconception that the cosine inverse of cosine should cancel each other out is a common trap for students, but the order of operations and restrictions must be considered.
📐 When dealing with trigonometric compositions, it's crucial to understand the restrictions and not just simplify expressions based on initial assumptions.
🌟 The concept of a reference angle is introduced as a tool to simplify the process of finding values of trigonometric functions in different quadrants.
🍬 An example is given using 7π/4 to illustrate how to break down the angle into parts and find the reference angle (π/4), which is easier to remember.
📐 The cosine of 7π/4 and π/4 both yield the same x-coordinate value (√2/2), but their y-coordinate values differ due to their quadrant positions.
🔄 The script emphasizes the importance of the reference angle in determining the correct quadrant and sign of the trigonometric function value.
🤔 The process of elimination based on the domain restrictions is highlighted, showing that only one of the two possible angles (π/4 or 7π/4) is the correct answer.
📊 The script visually contrasts the positions of the angles on the unit circle, showing that while they may have the same cosine value, their locations in the quadrants differ.
🚫 The mistake of not considering the domain restrictions when solving trigonometric problems is warned against, as it can lead to incorrect solutions.
📈 The script concludes with the reminder that understanding the restrictions is essential for selecting the correct angle from multiple possibilities in trigonometry.

Q & A

Why is it a common mistake for students to think that the cosine inverse of cosine should cancel each other out?
-Students often assume that the cosine inverse and cosine functions are inverses of each other and thus should cancel out when applied to the same value. However, this overlooks the importance of the order of operations and the restrictions that apply to the cosine function, especially when dealing with angles outside the principal range.
What is the significance of following the order of operations in trigonometric compositions?
-Following the order of operations is crucial because it ensures that the mathematical expressions are evaluated correctly, especially when dealing with functions like cosine and their inverses. Ignoring the order can lead to incorrect results and misunderstandings about the relationships between angles and their trigonometric values.
How does the concept of a reference angle help in understanding trigonometric values?
-A reference angle is a smaller, equivalent angle that can be used to find the trigonometric values of larger angles more easily. By using the reference angle, one can quickly determine the value of a trigonometric function without having to deal with complex calculations, making it easier to remember and apply in problem-solving.
What is the reference angle for 7π/4, and how does it relate to the original angle?
-The reference angle for 7π/4 is π/4 because 7π/4 can be expressed as 2π + π/4, which means it is equivalent to π/4 plus two full rotations (4π). The reference angle helps in determining the quadrant and sign of the trigonometric values for the original angle.
Why is it important to consider the quadrant when evaluating trigonometric functions?
-The quadrant in which an angle lies determines the signs of the trigonometric functions. For instance, cosine is positive in the first and fourth quadrants but negative in the second and third. Therefore, knowing the quadrant is essential for accurately evaluating the trigonometric values of an angle.
How does the restriction on the domain of cosine affect the solutions for the inverse cosine function?
-The inverse cosine function is only defined for values between -1 and 1, which corresponds to angles between 0 and π (0 to 180 degrees). This restriction ensures that the solutions for the inverse cosine are valid and within the principal range of the cosine function.
What are the two possible angles that produce a cosine value of √2/2, and how do you determine the correct one?
-The two angles that produce a cosine value of √2/2 are π/4 and 7π/4. To determine the correct angle, one must consider the quadrant in which the angle lies and the restrictions on the domain of the inverse cosine function. In this case, π/4 is within the principal range (0 to π), while 7π/4 is not.
How does the concept of the unit circle help in solving trigonometric problems?
-The unit circle is a visual tool that represents all angles and their corresponding trigonometric values. It helps in visualizing the relationship between angles and their sine, cosine, and tangent values, making it easier to solve problems by directly observing the coordinates of points on the unit circle.
What is the relationship between the cosine value of an angle and its reference angle on the unit circle?
-The cosine value of an angle on the unit circle is equal to the x-coordinate of the corresponding point. The reference angle's cosine value is the same as the original angle's cosine value because the reference angle is a smaller equivalent angle within the principal range that has the same trigonometric values as the original angle.
Why do some trigonometric functions have multiple solutions for a given value?
-Some trigonometric functions, like cosine and sine, have multiple solutions for a given value because the unit circle is periodic. This means that the same trigonometric value can occur at different angles, and the restrictions on the domain and range of the function must be considered to select the correct solution.
How does the concept of quadrants affect the sign of the trigonometric functions?
-The sign of the trigonometric functions is determined by the quadrant in which the angle lies. For example, cosine is positive in the first and fourth quadrants, negative in the second and third; sine is positive in the first and second quadrants, and negative in the third and fourth. This pattern is essential for solving trigonometric problems accurately.

Outlines

00:00

📚 Understanding the Cosine Inverse Function

This paragraph delves into the common misconception students have when dealing with the cosine inverse function in trigonometry. It emphasizes the importance of following the order of operations and not simply canceling out terms, as this could lead to incorrect conclusions. The speaker uses the example of cosine of 7 pi over 4 to illustrate how to find the reference angle and determine its quadrant, which is crucial for correctly applying the cosine inverse function. The explanation highlights the need to remember that the cosine inverse is only valid within the domain of zero to pi, and the final answer must adhere to this restriction.

05:00

🔍 Applying Restrictions to Trigonometric Functions

The second paragraph focuses on the concept of restrictions in trigonometry, particularly for the cosine function. The speaker clarifies that the inverse of sine is only a function when the domain of cosine is restricted between zero and pi. The discussion revolves around understanding why certain angles, like 7 pi over 4, are not valid solutions despite yielding the same cosine value as other angles within the restricted domain. The speaker uses visual aids, such as the unit circle, to explain how restrictions help in selecting the correct angle from multiple possibilities, which is essential for accurate problem-solving in trigonometry.

Mindmap

Keywords

💡Composition

In mathematics, composition refers to the process of performing operations in a specific order, as dictated by the rules of operations. In the context of the video, the speaker emphasizes the importance of following the order of operations when dealing with trigonometric functions, such as cosine, to avoid incorrect simplifications or cancellations.

💡Cosine Inverse

The cosine inverse, also known as arccosine or cos^(-1), is the inverse function of the cosine function. It is used to find the angle whose cosine is a given value. In the video, the cosine inverse is used to solve for an angle when the value of the cosine function is known, but the speaker warns against assuming that the inverse function will always undo the original function without considering the quadrant in which the angle lies.

💡Order of Operations

The order of operations is a set of rules that dictates the sequence in which mathematical operations should be performed. In the video, the speaker stresses the importance of adhering to this order when working with trigonometric functions to arrive at the correct solution.

💡Reference Angle

A reference angle is the acute angle formed with the x-axis by a line making an angle with the negative x-axis. It is used to find the values of trigonometric functions for angles in other quadrants by relating them to angles in the first quadrant. In the video, the reference angle is used to determine the cosine value of an angle and to identify the correct quadrant for the angle.

💡Unit Circle

A unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane. It is a fundamental tool in trigonometry for defining trigonometric functions and their inverses. In the video, the unit circle is implicitly used to discuss the cosine values and reference angles.

💡Quadratic

Quadratic refers to a mathematical expression, equation, or function that has the highest power of the variable as 2. In the context of the video, the term 'square root of 2 over 2' is an example of a quadratic term, as it involves a square root, which is the second power.

💡Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. It is used to solve for unknown angles and lengths in various mathematical and real-world problems. In the video, trigonometry is the central topic, with the speaker discussing the properties and applications of trigonometric functions like cosine.

💡Domain and Range

In the context of functions, the domain is the set of all possible input values, while the range is the set of all possible output values. The video touches on the importance of restricting the domain of certain functions, like the cosine inverse, to ensure they return valid outputs.

💡Quadrants

In a two-dimensional coordinate system, the quadrants are the four regions defined by the intersection of the positive and negative x and y axes. Quadrants are numbered counterclockwise, starting from the upper right, which is the first quadrant. In the video, the concept of quadrants is used to determine the sign of trigonometric function values based on the angle's location.

💡Restrictions

In mathematics, restrictions refer to the limitations or conditions placed on variables or functions to ensure they have meaningful values or to simplify the problem-solving process. In the video, the speaker discusses the importance of considering restrictions when solving trigonometric problems to ensure that the solutions are valid within the given context.

💡Sine and Cosine

Sine and cosine are two of the six trigonometric functions that relate angles to the ratios of sides in a right triangle. They are fundamental to the study of trigonometry and are used to find the values of unknown angles and sides. In the video, the speaker focuses on cosine but also mentions sine, noting that both can have multiple solutions based on the quadrant of the angle.

Highlights

Students often fall into the trap of assuming that the cosine inverse of cosine should cancel each other out, which is not always the case.

The importance of following the order of operations in composition problems related to trigonometric functions.

The concept of the reference angle and how it simplifies the process of finding the value of trigonometric functions.

The method of breaking down 7 pi over 4 into parts to understand its relation to the unit circle.

The process of finding the cosine of pi over four using the reference angle method.

The explanation of how the cosine inverse of a value can yield two different angles due to the nature of the unit circle.

The distinction between the two angles that produce the same cosine value and the method to determine the correct one based on quadrant restrictions.

The emphasis on the need to remember the restrictions of the domain of cosine to correctly solve problems.

The practical application of the reference angle in quickly finding the value of trigonometric functions in different quadrants.

The discussion on how the same x value on the unit circle can correspond to different angles and the importance of quadrant restrictions in choosing the correct angle.

The clarification that while cosine and sine can have two possible values, tangent can also have two values, and the solution must adhere to the given restrictions.

The strategy of solving the innermost problem first and then proceeding to the next, which is a methodological approach to problem-solving in trigonometry.

The illustration of how the reference angle simplifies the process of remembering trigonometric values, especially in the first quadrant.

The detailed explanation of the relationship between the reference angle and the actual angle in the context of the unit circle and quadrant restrictions.

The emphasis on the necessity of understanding the restrictions to correctly apply the concepts of trigonometric functions in problem-solving.

The practical demonstration of how to use the reference angle to find the correct angle within the given restrictions, which is crucial for solving trigonometric composition problems.

Transcripts

Browse More Related Video

Pythagorean Identities - Examples & Practice Problems, Trigonometry

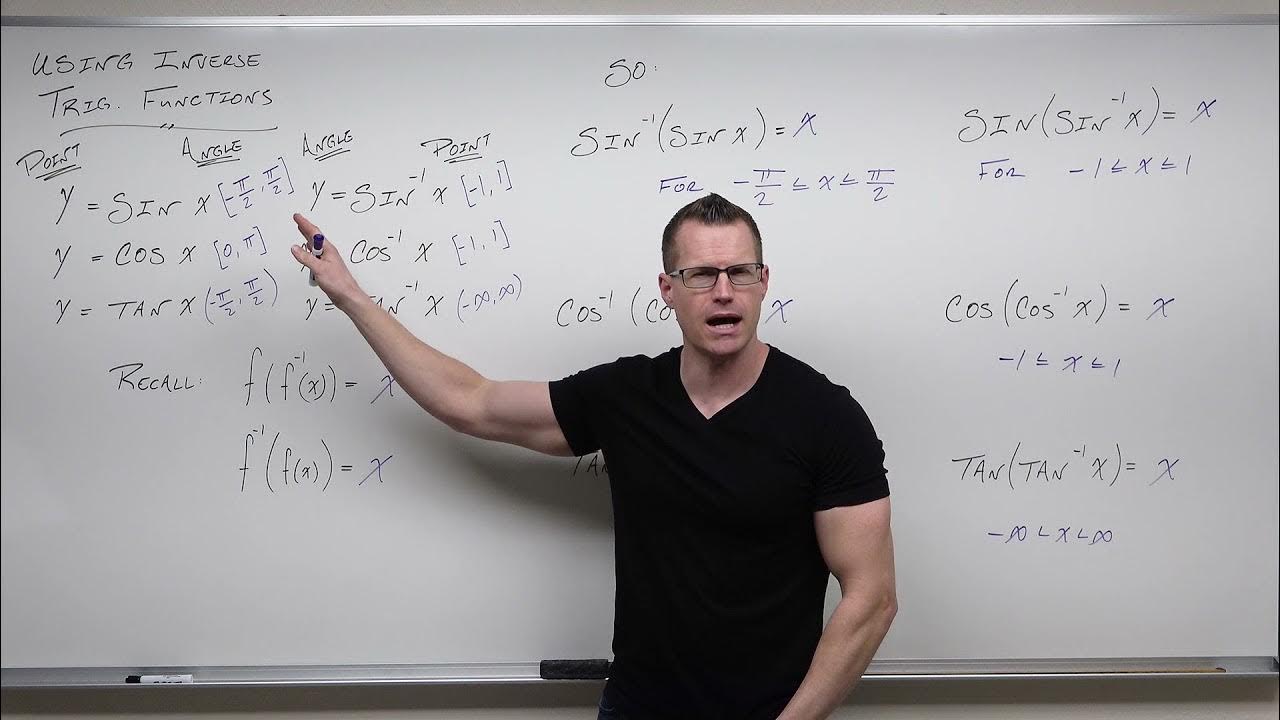
How to Use Inverse Trigonometric Functions (Precalculus - Trigonometry 18)

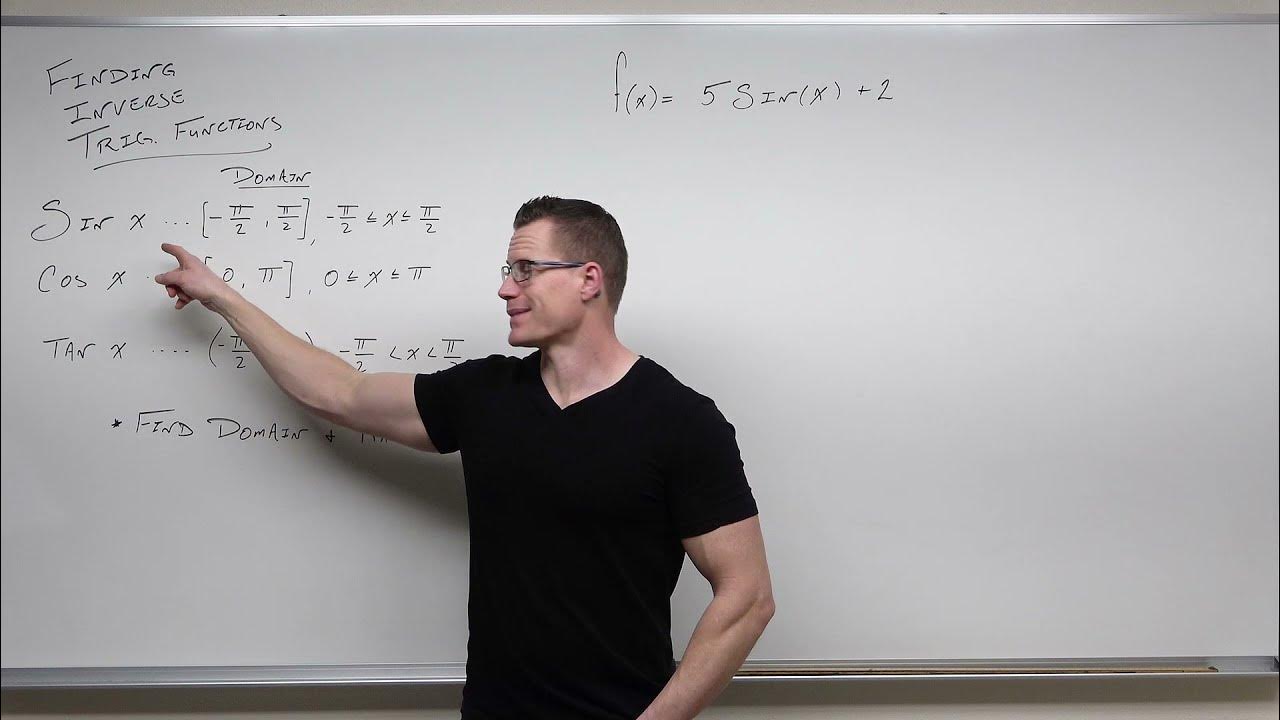
How to Find Inverse Trigonometric Functions (Precalculus - Trigonometry 19)

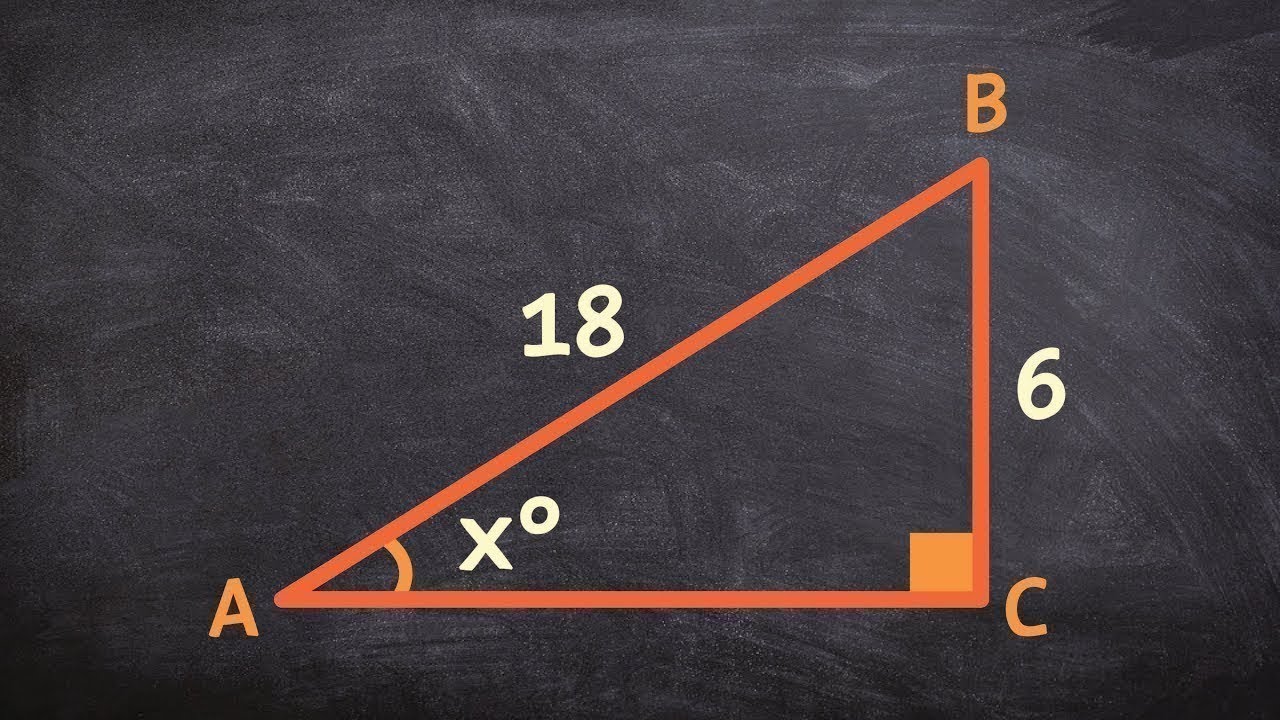
Learn to find the missing angles for a triangle using inverse trig functions

Using Sum and Difference Formulas in Trigonometry (Precalculus - Trigonometry 26)

Evaluate Inverse Trig Functions - Step by Step

How to evaluate for the composition of two trigonometric functions

Takeaways

Q & A

Why is it a common mistake for students to think that the cosine inverse of cosine should cancel each other out?

What is the significance of following the order of operations in trigonometric compositions?

How does the concept of a reference angle help in understanding trigonometric values?

What is the reference angle for 7π/4, and how does it relate to the original angle?

Why is it important to consider the quadrant when evaluating trigonometric functions?

How does the restriction on the domain of cosine affect the solutions for the inverse cosine function?

What are the two possible angles that produce a cosine value of √2/2, and how do you determine the correct one?

How does the concept of the unit circle help in solving trigonometric problems?

What is the relationship between the cosine value of an angle and its reference angle on the unit circle?

Why do some trigonometric functions have multiple solutions for a given value?

How does the concept of quadrants affect the sign of the trigonometric functions?