Using the Second Derivative (1 of 5: Finding the Point of Inflexion)

Eddie Woo
13 Dec 201511:01
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the concept of derivatives in calculus, focusing on the interpretation of the first and second derivatives. It explains that the first derivative indicates the rate of change or gradient, while the second derivative reveals the concavity, which is akin to the curvature of a function. The script uses geometric analogies to illustrate how different increasing functions can have varying rates of increase, thus different concavities. It further explains how to find stationary points by setting the first derivative to zero and using the second derivative to determine the nature of these points, whether they are maxima, minima, or points of inflection. The importance of understanding the connection between the algebraic and geometric interpretations of derivatives is emphasized.

Takeaways
  • 📈 The first derivative represents the gradient or slope of a function, which is related to the function's increasing or decreasing behavior.
  • 📉 The second derivative indicates concavity, which is about the curvature of a function and can tell us if a function is concave up or concave down.
  • 🔍 A function that is increasing at a constant rate, getting faster, or getting slower can be described as having different concavities: constant rate implies no curvature, getting faster implies concave up, and getting slower implies concave down.
  • ✅ A straight line, which can be described by the equation y = mx + b, has a first derivative equal to the constant m and a second derivative of zero, indicating no concavity.
  • 🔺 Concave up means the second derivative is positive, which corresponds to a minimum point in the function.
  • 🔻 Concave down means the second derivative is negative, indicating a maximum point in the function.
  • 🧮 To find stationary points, set the first derivative (f') to zero and solve for x, then determine the y values for these x coordinates.
  • 🔍 The nature of a stationary point can be determined by examining the sign of the second derivative (f'') at that point.
  • 📊 A positive second derivative at a stationary point indicates a minimum turning point, while a negative second derivative indicates a maximum turning point.
  • 🔴 It is important to state the sign of the second derivative and connect it to the geometric concept of concavity to fully understand the nature of the stationary point.
  • ⚖️ The process of finding and classifying stationary points using derivatives is a critical step in analyzing the features of a graph.
Q & A

  • What is the focus of last week's lesson?

    -The focus of last week's lesson was on finding the second derivative and understanding what it tells us about a function's concavity.

  • What does the first derivative of a function represent?

    -The first derivative of a function represents the gradient, which is related to the geometry and shape of the function.

  • What does the second derivative of a function indicate?

    -The second derivative of a function indicates concavity, which describes the curvature and the direction in which the function is facing.

  • How can concavity be used to differentiate between increasing functions?

    -Concavity can be used to differentiate between increasing functions by observing whether they are increasing at a constant rate (straight line), increasing faster, or increasing slower.

  • What does it mean when a function is concave up?

    -When a function is concave up, it means the second derivative is positive, indicating the curvature is facing upwards.

  • What does it mean when a function is concave down?

    -When a function is concave down, it means the second derivative is negative, indicating the curvature is facing downwards.

  • How can you determine the concavity of a straight line?

    -A straight line has no curvature, so its second derivative is zero, indicating it has no concavity.

  • What is the relationship between stationary points and the first derivative?

    -Stationary points occur where the first derivative is zero because the gradient is neither increasing nor decreasing at these points.

  • How can the second derivative be used to determine the nature of stationary points?

    -The second derivative can determine the nature of stationary points by indicating concavity. If the second derivative is positive at a stationary point, it's a minimum (concave up). If it's negative, it's a maximum (concave down).

  • What steps should be followed to classify stationary points using the second derivative?

    -First, find the first derivative and set it to zero to locate stationary points. Then, calculate the second derivative and evaluate it at the stationary points. Use the sign of the second derivative to classify each stationary point as a maximum or minimum.

Outlines
00:00
📈 Understanding Derivatives and Concavity

The first paragraph introduces the concept of derivatives in the context of geometry and shape. It explains that the first derivative is related to the gradient or slope of a curve, while the second derivative is about concavity, which concerns the curvature of the function. The speaker uses examples of increasing functions with different rates of increase to illustrate the concept of concavity. They clarify that a straight line, represented by y = mx + b, has a second derivative of zero, indicating no curvature. The paragraph concludes with a discussion on how the second derivative can be used to identify and understand stationary points on a graph, and how to determine their nature by examining the sign of the second derivative.

05:02
🔍 Identifying Stationary Points and Their Nature

The second paragraph delves into the process of finding stationary points, which are locations where the first derivative (gradient) is zero. It emphasizes the importance of understanding the context and the connecting sentences when solving mathematical problems. The speaker provides a step-by-step method to find the x and y values of stationary points using the given function. They then explain how to determine the nature of these points using the second derivative. If the second derivative is positive, the point is a minimum (concave up), and if it's negative, the point is a maximum (concave down). The speaker illustrates this with the given function, calculating the second derivative and using it to identify the nature of the stationary points as a minimum turning point at (1, -2) and a maximum turning point at (-1, 2).

10:04
🔢 Applying Second Derivatives to Analyze Stationary Points

The third paragraph summarizes the process of using the second derivative to determine the nature of stationary points. It reiterates the importance of understanding the relationship between the sign of the second derivative and the concavity of the function, which in turn indicates whether a stationary point is a maximum or minimum. The speaker emphasizes the significance of stating the findings clearly and the risk of omitting steps, as it could lead to a misunderstanding of the problem. The paragraph concludes by reinforcing the method of analyzing the second derivative at specific points to classify stationary points as maximum or minimum, and the importance of connecting all the elements of the problem for a comprehensive understanding.

Mindmap
Keywords
💡First Derivative
The first derivative in calculus represents the rate at which a function is changing at any given point. It is a measure of the slope of the tangent line to the function's graph at a particular point. In the context of the video, the first derivative is used to determine the gradient of a function, which is essential for understanding the function's increasing or decreasing nature. For example, the script mentions that the first derivative is 'about gradient like, we're talking about geometry and shape'.
💡Second Derivative
The second derivative is the derivative of the first derivative. It provides information about the concavity of a function and the rate of change of the slope. In the video, the second derivative is explained as being 'about concavity' and is used to determine whether a function is concave up or concave down. The script states that 'second derivative is about, concavity so we introduced this idea, that you know rather than going up or, going down increasing or decreasing or, neither stationary, concavity is about thinking about the, curvature in which way it's facing'.
💡Gradient
Gradient refers to the slope of a line or curve at a particular point. In the context of the video, the gradient is associated with the first derivative and is used to describe whether a function is increasing or decreasing. The script uses the term 'gradient' to explain the rate at which a function is changing, as in 'first derivative is about gradient like, we're talking about geometry and shape'.
💡Concavity
Concavity is a concept in calculus that describes the curvature of a function. A function is said to be concave up if it curves upward like the shape of a cup and concave down if it curves downward like the shape of a cap. The script explains concavity in relation to the second derivative, stating 'concave up means the second derivative is positive okay concave down means the, second derivative is negative'.
💡Stationary Points
Stationary points are points on a function where the first derivative is zero or undefined, indicating a potential maximum, minimum, or point of inflection. In the video, the concept of stationary points is discussed in relation to finding and classifying these points using the first and second derivatives. The script instructs to 'find stationary points so you solve for, the first root of being zero and then determine their nature'.
💡Increasing Function
An increasing function is one where the output values increase as the input values increase. The video script uses the concept of increasing functions to illustrate different rates of increase and their concavity. It mentions 'here's an increasing function here's, another increasing function okay but, when you think about these three good, morning, when you think about each of these three, even though they're all increasing, they're all increasing in different ways'.
💡Decreasing Function
A decreasing function is one where the output values decrease as the input values increase. The script does not explicitly use the term 'decreasing function', but it is implied when discussing the nature of stationary points and the behavior of functions that are not increasing. The concept is relevant to understanding the overall theme of the video, which is about analyzing the behavior of functions using derivatives.
💡Linear Function
A linear function is a function that has a constant rate of change and can be represented by a straight line when graphed. The script introduces the concept of a linear function with the equation 'y equals m x plus b' and explains that its first derivative is the gradient 'm', and its second derivative is zero, indicating no curvature.
💡Odd Function
An odd function is a function that satisfies the condition f(-x) = -f(x) for all x in the domain of the function. The video script mentions symmetry in the context of an odd function, stating 'what kind of symmetry does this, function have it's an, odd function, you can easily like it's all they're all, all the powers are odd'. This concept is used to predict the y-values of stationary points found at x = 1 and x = -1.
💡Turning Points
Turning points on a graph are points where the function changes direction, either from increasing to decreasing or vice versa. The video discusses how to determine the nature of turning points using the second derivative. It mentions 'is a minimum turning point' and 'is a maximum' in relation to the concavity at those points, which is determined by the sign of the second derivative.
Highlights

The first derivative is related to the gradient, which is a concept in geometry and shape.

The second derivative is associated with concavity, indicating the curvature of a function.

Different increasing functions can have different concavities, such as constant rate, increasing faster, or increasing slower.

A function can be concave up, concave down, or neither, depending on its curvature.

A straight line has no curvature and is characterized by a second derivative of zero.

Concave up indicates a positive second derivative, while concave down indicates a negative one.

Stationary points are where the first derivative is zero.

The nature of stationary points can be determined by examining the sign of the second derivative.

A table of values can be used to pick appropriate x-values for determining the nature of stationary points.

The second derivative provides a more efficient tool for finding and determining the nature of stationary points.

An example function is given to illustrate finding stationary points and their nature using derivatives.

The function f(x) = x^3 - 3x has stationary points at x = 1 and x = -1.

The y-coordinates of the stationary points are -2 and 2, respectively.

The second derivative test uses the sign of the second derivative to determine if a point is a maximum or minimum.

A positive second derivative at a point indicates a minimum turning point, while a negative indicates a maximum.

The importance of stating the connection between the second derivative's sign and the nature of the turning point.

The second derivative test is a critical method for analyzing the features of a graph.

Transcripts

Browse More Related Video

Concavity introduction | Using derivatives to analyze functions | AP Calculus AB | Khan Academy

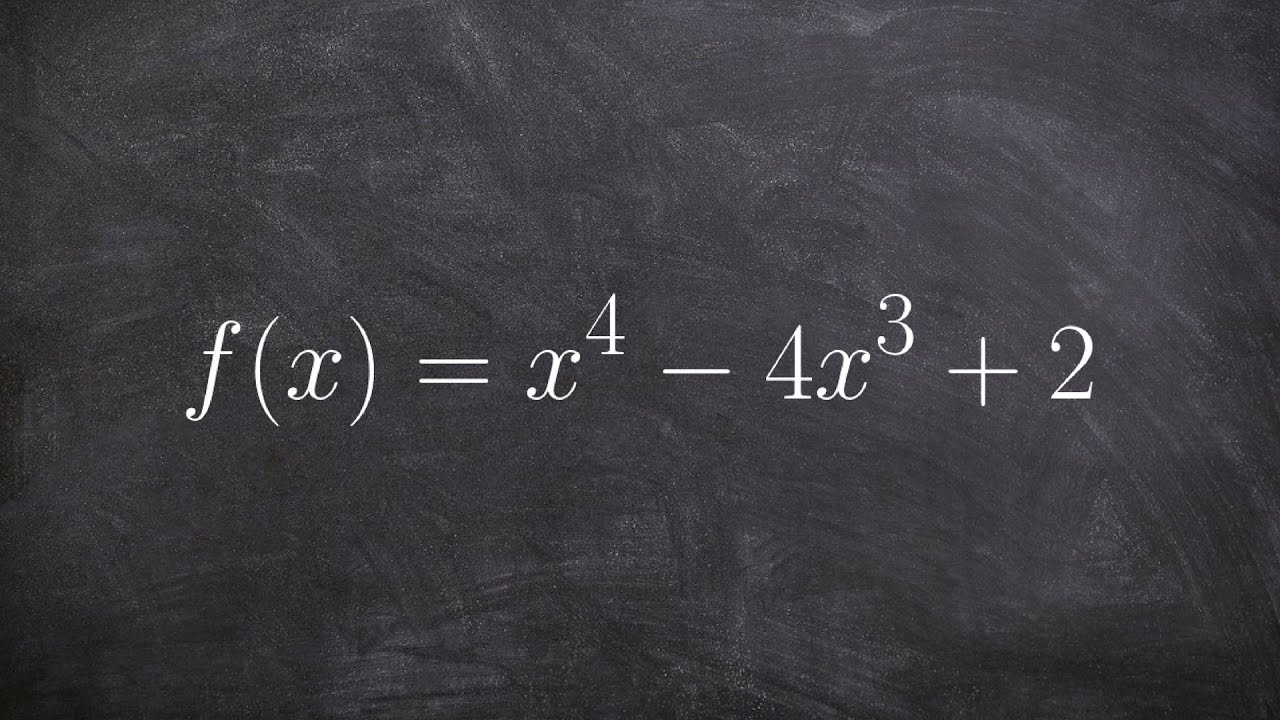
Learn how to determine concavity and point of inflection AP style

3.2 - Using Second Derivatives to Classify Max and Min Values

What the Second Derivative Tells Us

Business Calculus - Math 1329 - Section 3.2 - Concavity and Points of Inflection

Concavity, Inflection Points, Increasing Decreasing, First & Second Derivative - Calculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ConcavityDerivativesStationary PointsGraph AnalysisGeometryCalculusMathematicsFunction BehaviorCurvatureEducational Content