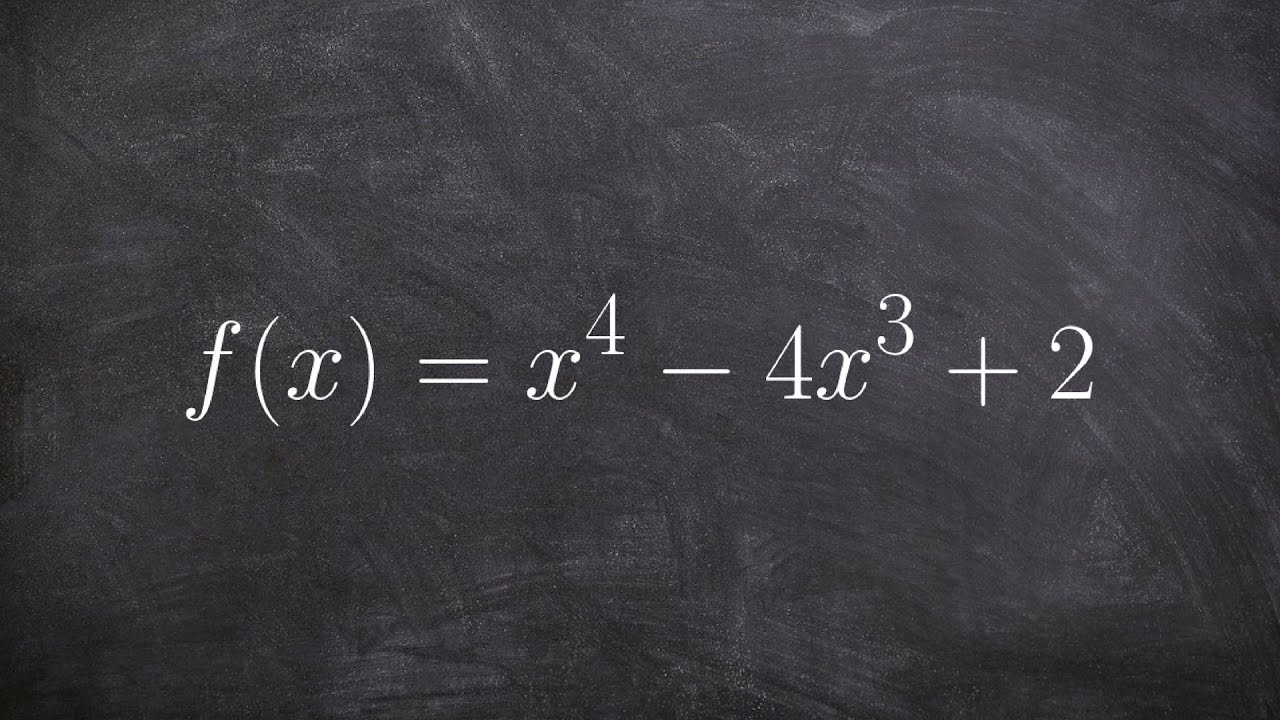Business Calculus - Math 1329 - Section 3.2 - Concavity and Points of Inflection
TLDRThis video script delves into the mathematical concepts of concavity and points of inflection, using the first and second derivatives of functions to determine their behavior. The presenter clarifies the difference between a function increasing and its first derivative increasing, which is key to identifying concavity. The script explores how concavity relates to the shape of a curve, with examples to illustrate concave up and concave down functions. The process for determining intervals of concavity and finding inflection points is outlined, involving finding where the second derivative is zero or undefined, creating a sign chart, and evaluating the function at critical points. Several examples are worked through, demonstrating how to find derivatives, solve for critical points, and use the second derivative to assess concavity and locate inflection points. The script also touches on the business concept of diminishing returns, applying the mathematical analysis to real-world scenarios like advertising spend and sales, and concludes with a practical example of finding the maximum rate of change in sales related to advertising expenditure.
Takeaways
- 📈 The concept of concavity is determined by the behavior of a function's first derivative. If the first derivative is increasing, the function is concave up; if it's decreasing, the function is concave down.
- 🔍 To understand concavity, one must differentiate between the function's increase and the first derivative's increase. The function can be increasing or decreasing while its first derivative is increasing alone.
- 📌 Concavity relates to the shape of the graph of a function; a function is concave up if it opens upward like a bowl, and concave down if it opens downward like an inverted bowl.
- 📐 The sign of the second derivative helps determine concavity: a positive second derivative indicates concave up, while a negative second derivative indicates concave down.
- 🔑 Inflection points are the points on the graph where the concavity changes. These are found by determining where the second derivative is zero or undefined.
- 🧮 To find intervals of concavity, one must find the second derivative, solve it for zero, and use the solutions to create a sign chart for the second derivative.
- 🤔 The second derivative test is used to determine relative extrema: a positive second derivative at a critical point indicates a relative minimum, while a negative value indicates a relative maximum.
- 📊 For business applications, such as advertising, the point of diminishing returns can be found by analyzing the inflection point of the sales function, which represents the point where the rate of increase in sales from advertising begins to decrease.
- 💡 The maximum rate of change in sales (or the point of maximum effectiveness of advertising) can be found by evaluating the first derivative at the inflection point.
- ✏️ The process of finding the second derivative involves applying the power rule and chain rule, and then simplifying the expression to a rational function.
- 📉 In the context of business, the point of diminishing returns is where additional advertising spending yields less incremental sales, indicating a change from the steepest increase to a slower rate of growth in sales.
Q & A
What is the definition of concavity in mathematical functions?
-Concavity refers to the curvature of a function's graph. A function is said to be concave up if its first derivative is increasing, and concave down if its first derivative is decreasing.
How does the first derivative relate to concavity?
-The first derivative of a function indicates the slope of the tangent line at any given point on the function's graph. If the first derivative is increasing, the function is concave up; if it's decreasing, the function is concave down.
What is an inflection point in a function?
-An inflection point is a point on the graph of a function where the concavity changes, i.e., the function transitions from concave up to concave down or vice versa.
How can you determine if a function is concave up or down on a certain interval?
-To determine the concavity on an interval, you first find the second derivative of the function. If the second derivative is positive on an interval, the function is concave up; if it's negative, the function is concave down.
What is the process for finding the concavity of a given function?
-To find the concavity of a function, first find the first and second derivatives. Then, identify the intervals where the second derivative is positive or negative and any points that are inflection points, which are where the second derivative is zero or undefined.
How does the concept of concavity relate to the shape of a parabola?
-A parabola that opens upwards is an example of a concave up shape, while a parabola that opens downwards is an example of a concave down shape.
What is the point of diminishing returns in a business context?
-The point of diminishing returns refers to the stage in business where additional investment leads to lower incremental returns. For example, as more money is spent on advertising, the increase in sales may start out strong but eventually levels off, indicating that each additional dollar spent is bringing in fewer additional sales.
How can you find the point of diminishing returns for a given sales model?
-To find the point of diminishing returns, you need to analyze the rate of change (first derivative) of the sales model. The point of diminishing returns occurs when the rate of change starts to decrease, indicating that the investment is no longer yielding as much additional return as before.
What is the maximum rate of change in sales according to the example in the script?
-In the given example, the maximum rate of change in sales occurs at $10,000 in advertising cost, where for every additional thousand dollars spent, an additional 400 stereos in sales are gained.
How can the second derivative test be used to determine the nature of critical points in a function?
-The second derivative test can help determine whether a critical point is a relative maximum, relative minimum, or neither. If the second derivative evaluated at a critical point is positive, the function is concave up and the critical point is a relative minimum. If it's negative, the function is concave down and the critical point is a relative maximum. If the second derivative is zero or undefined, the test is inconclusive.
Outlines
📈 Understanding Concavity and Points of Inflection
This paragraph introduces the concepts of concave up and concave down functions, relating them to the behavior of the first derivative. It explains that if the first derivative is increasing, the function is concave up, and if it's decreasing, the function is concave down. The paragraph uses the analogy of a bowl shape to illustrate concavity. It also includes an example with a hand-drawn function and estimated slopes of tangent lines at various points to demonstrate how concavity can be determined from the first derivative's changes.
📊 Determining Concavity and Inflection Points
The second paragraph outlines the method for determining intervals where a function is concave up or down. It involves finding where the second derivative is zero or undefined, creating a sign chart, and using the sign of the second derivative to determine concavity. An inflection point is identified as a point where the function changes concavity. The process is demonstrated with an example function, and the second derivative is used to find the concavity intervals and the location of an inflection point.
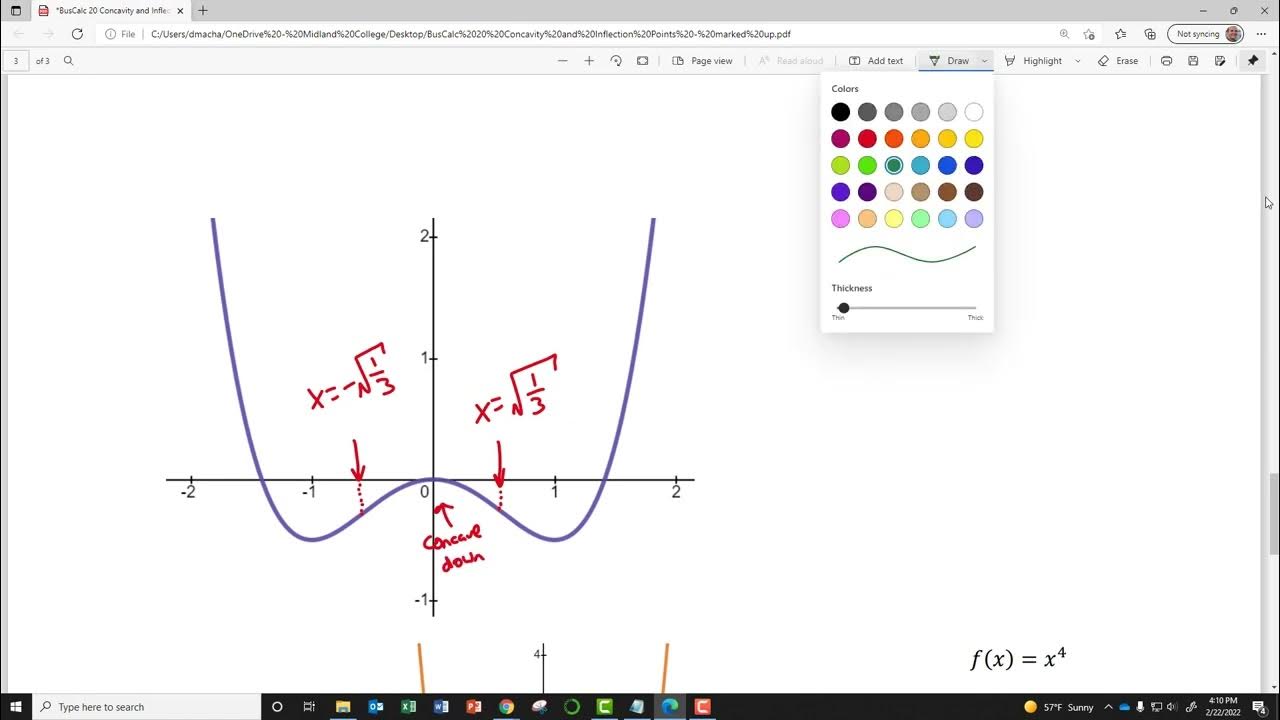
🔢 Solving for Concavity and Inflection Points with Polynomial Functions
This paragraph deals with determining the concavity of a polynomial function and finding its inflection points. It begins by finding the first and second derivatives of the given function. The zeros of the second derivative are found, and a sign chart is created to determine the intervals of concavity. The function's concavity is established, and the points where concavity changes are identified as inflection points. The process is illustrated with a detailed example.
🧮 Analyzing the Second Derivative for Concavity
The fourth paragraph focuses on using the second derivative to analyze the concavity of a function. It explains that the second derivative being positive indicates concave up, while a negative second derivative indicates concave down. The paragraph also addresses undefined second derivatives and how they can affect the analysis. An example is provided to demonstrate the process of finding the second derivative, creating a sign chart, and determining the concavity and inflection points.
🔍 Examining the Domain and Concavity of Rational Functions
This paragraph discusses the domain of a rational function and how to find it by setting the denominator equal to zero. It then proceeds to find the first and second derivatives of the function and uses these to analyze concavity. The paragraph explains that the domain being all real numbers means there are no restrictions on the variable. The process of finding the second derivative and using it to determine concavity is demonstrated, and the concept of an undefined second derivative is clarified.
📚 Derivatives and Simplifying Rational Functions
The sixth paragraph is about finding the first and second derivatives of a given function using the quotient rule and chain rule. It emphasizes the importance of simplifying the derivatives into a rational, simplified function. The process involves factoring out common terms and multiplying parts together to get a simplified expression for the second derivative. The paragraph also discusses the conditions under which the second derivative is undefined and how to find where it equals zero.
🔗 Applying Grouping and Factoring to Second Derivatives
The seventh paragraph delves into the technique of grouping to factor a second derivative expression. It demonstrates how to factor out common terms and how the process of grouping can reveal factors that can be pulled out of the expression. The paragraph shows how to set the second derivative equal to zero and solve for the variable to find potential inflection points. It also discusses how multiplicities can be used to determine the sign of the second derivative across different intervals.
📉 The Second Derivative Test and Business Applications
The eighth paragraph explains the second derivative test, which is used to determine critical values that could represent relative maxima or minima. It outlines the conditions under which the second derivative test is conclusive and when it is inconclusive. The concept of the point of diminishing returns in business is introduced, using advertising expenditure and sales as an example. The paragraph shows how to find the point of diminishing returns by identifying the inflection point of the sales function.
📈 Maximizing Advertising Efficiency with the Second Derivative
The ninth paragraph applies the concepts of derivatives to a business scenario where a company is looking to maximize the return on advertising investment. It discusses finding the maximum rate of change in sales related to advertising expenditure. The paragraph demonstrates how to calculate the first derivative to find the rate of change in sales and how to identify the maximum rate of change at the inflection point. It concludes with the interpretation of the maximum rate in the context of advertising efficiency.
🎓 Comprehensive Summary of Derivatives in Business and Mathematics
The final paragraph provides a comprehensive summary of the use of derivatives in both mathematical analysis and business applications. It ties together the concepts of concavity, inflection points, and the second derivative test with practical examples such as advertising and sales. The paragraph emphasizes the importance of understanding these mathematical tools to make informed decisions in business, particularly in optimizing investment outcomes.
Mindmap
Keywords
💡Concavity
💡Derivative
💡Inflection Point
💡Second Derivative
💡Tangent Line
💡Quotient Rule
💡Chain Rule
💡Critical Value
💡Point of Diminishing Returns
💡Max Rate of Change
💡Product Rule
Highlights
Section 3.2 introduces the concept of concavity, focusing on how a function's first derivative influences its concave up or down behavior.
A function is considered concave up if its first derivative is increasing, and concave down if the first derivative is decreasing.
The difference between a function increasing and its first derivative increasing is clarified, emphasizing the derivative's role in concavity.
The relationship between concavity and the shape of a curve, such as a parabola, is explained using the bowl and ball analogy.
An example illustrates how to determine the slopes of tangent lines at various points to understand a function's concavity.
The process for determining intervals where a function is concave up or down involves finding the second derivative's zero or undefined points.
A sign chart is used to analyze the second derivative's sign within intervals to classify the function's concavity.
Inflection points, where a function changes concavity, are identified as critical points on the graph.
The concavity of a function f(x) = -x^3 - 6x^2 + 18x + 5 is determined using the second derivative, revealing an inflection point at x = -2.
For the function f(x) = x^5 - 3x^6 + 27, the second derivative is used to find inflection points at x = 0 and x = 2/9.
The second derivative of f(x) = -5x - 2^(2/5) is found to be always positive, indicating the function is concave up with an inflection point at x = 2.
The function f(x) = (x - 1) / (x^2 - 4x + 5) has its domain and concavity analyzed, with the second derivative used to find inflection points.
The concept of the second derivative test for relative extrema is explained, with examples demonstrating how to apply it.
The point of diminishing returns in business, particularly in advertising, is discussed in relation to the inflection point of a sales function.
An example problem calculates the point of diminishing returns for a stereo sales function, identifying the maximum rate of change in sales at $10,000 in advertising costs.
The maximum rate of change in sales, equivalent to the slope of the tangent line at the inflection point, is used to determine the most effective advertising spend.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: