Concavity, Inflection Points, Increasing Decreasing, First & Second Derivative - Calculus

The Organic Chemistry Tutor

28 Sept 201654:17

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the analysis of a function's behavior, focusing on key concepts such as intervals of increase and decrease, concavity, inflection points, and critical points. It explains how the first derivative's sign indicates whether a function is increasing or decreasing and how the second derivative's sign reveals concavity. The script uses examples to illustrate the first derivative test for local extrema and inflection points, emphasizing the importance of understanding these concepts for a comprehensive grasp of calculus.

Takeaways

📈 A function is increasing when its first derivative is positive, and decreasing when the first derivative is negative.
🔄 The first derivative being zero indicates a constant function, where the function neither increases nor decreases.
🔺 Local maximum and minimum values occur when the first derivative changes from positive to negative or vice versa.
🔄 Critical points occur where the first derivative is zero or does not exist, which can indicate local extrema or inflection points.
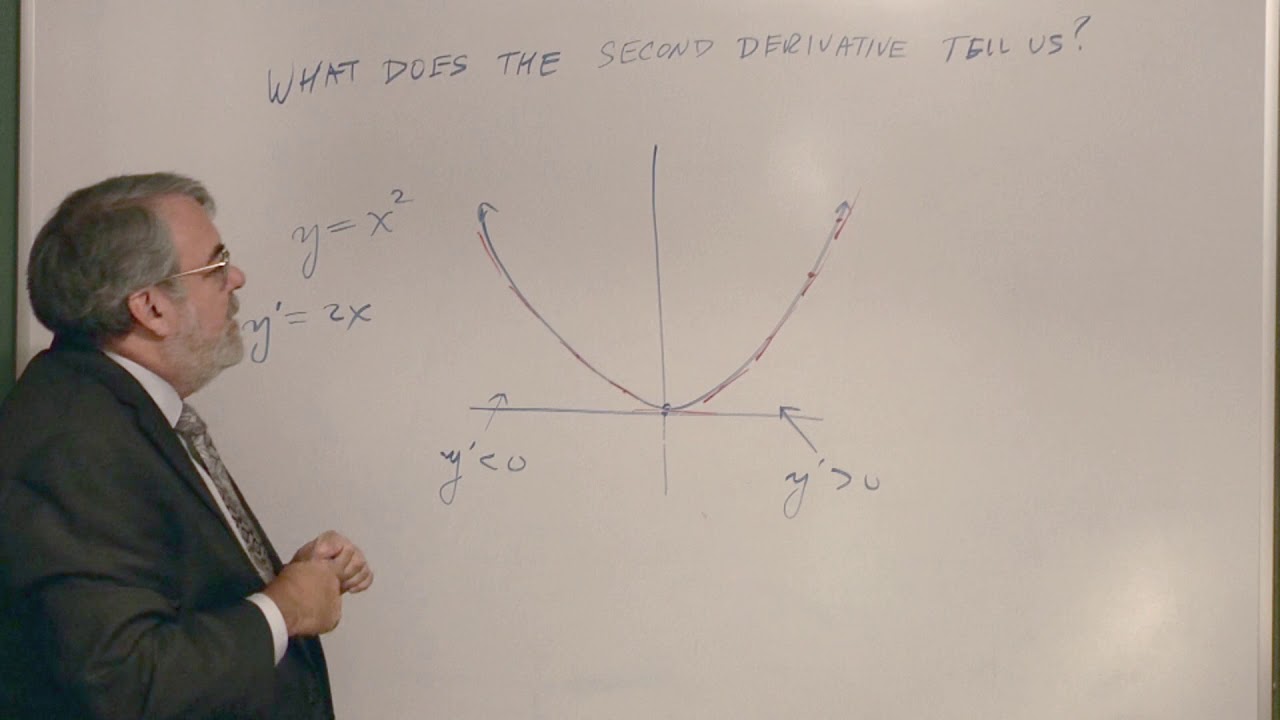
📊 Concavity is determined by the second derivative: positive for concave up and negative for concave down.
🔄 Inflection points occur when the second derivative crosses zero, indicating a change in concavity.
🌐 The slope of a function can increase or decrease, affecting the concavity of the function's graph.
📌 Examples and tests, such as the first derivative test, are used to analyze the behavior of functions regarding increases, decreases, and concavity.
🔢 Finding the intervals of increase and decrease involves creating a sign chart for the first derivative.
🔢 The second derivative can be used to determine the intervals of concavity up and down.
📈 The graph of a function can visually represent its increasing and decreasing intervals, critical points, local extrema, and inflection points.

Q & A

What is the relationship between the first derivative of a function and the function's increasing or decreasing behavior?
-The first derivative of a function indicates the slope of the function at any given point. If the first derivative is positive, the function is increasing at that point, and if it's negative, the function is decreasing.
How can you determine if a function has a local maximum or minimum based on the first derivative?
-A local maximum or minimum occurs where the first derivative changes sign. Specifically, a local maximum happens when the first derivative changes from positive to negative, and a local minimum occurs when it changes from negative to positive.
What are critical points in the context of a function and how do they relate to the first derivative?
-Critical points are points on the graph of a function where the first derivative is either zero or does not exist. These points are significant because they often indicate potential local maxima or minima, as well as points of discontinuity.
How does the concavity of a function relate to its second derivative?
-The concavity of a function is related to the sign of its second derivative. If the second derivative is positive, the function is concave up, and if it's negative, the function is concave down. The concavity indicates how the slope of the function's first derivative is changing.
What is an inflection point and how can you identify it?
-An inflection point is a point on the graph of a function where the concavity changes, meaning the second derivative crosses zero and the slope of the function changes from increasing to decreasing or vice versa. It can be identified when the second derivative is equal to zero and the concavity changes sign.
Given the function f(x) = x^(3/2) - 3x^2 + 5, how do you find the critical numbers?
-To find the critical numbers for the function f(x) = x^(3/2) - 3x^2 + 5, you first find the first derivative, set it equal to zero, and solve for x. The first derivative is (3/2)x^(1/2) - 6x. Setting this equal to zero gives the critical numbers x = 0 and x = 2.
What is the interval where the function f(x) = x^(3/2) - 3x^2 + 5 is increasing?
-The function f(x) = x^(3/2) - 3x^2 + 5 is increasing on the interval from negative infinity to 0 and from 2 to infinity. This is determined by the sign of the first derivative, which is positive in these intervals.
How do you determine if a function is concave up or concave down on a specific interval?
-To determine if a function is concave up or concave down on a specific interval, you examine the sign of the second derivative on that interval. If the second derivative is positive, the function is concave up; if it's negative, the function is concave down.
What is the role of the second derivative test in analyzing a function?
-The second derivative test is used to determine the concavity of a function, which helps identify inflection points. It also provides information about the nature of critical points, such as whether they represent local maxima, minima, or neither, based on the change in concavity.
Given the function f(x) = x^4/3 + 4x^(1/3), what are the intervals where the function is increasing and decreasing?
-For the function f(x) = x^4/3 + 4x^(1/3), the first derivative is (4/3)x^(1/3) + (4/3)x^(-2/3). The function is increasing on the interval from -1 to 0 and from 1 to infinity, and it is decreasing on the interval from negative infinity to -1 and from 0 to 1.
What is the domain of the function f(x) = sqrt(x + 4)?
-The domain of the function f(x) = sqrt(x + 4) is all real numbers greater than or equal to -4, since the square root function requires the radicand (the expression inside the square root) to be non-negative.

Outlines

00:00

📈 Understanding Function Behaviors

This paragraph introduces the concepts of intervals where a function is increasing or decreasing, concavity (concave up and down), inflection points, and critical points. It explains how the first derivative being positive or negative indicates whether a function is increasing or decreasing, and how the sign change in the first derivative can signal local maximum or minimum values. Critical points are defined as points where the first derivative is zero or undefined, and the paragraph concludes with an example of a graph that illustrates these concepts.

05:01

📊 Identifying Concavity and Inflection Points

The second paragraph delves into the determination of when a function is concave up or down, which depends on the sign of the second derivative. It describes how the first derivative's behavior reflects the concavity, with an increasing first derivative indicating concave up and a decreasing first derivative indicating concave down. The concept of inflection points is introduced as points where the concavity changes, signaled by the second derivative crossing zero and the concavity changing from positive to negative or vice versa. The explanation is supported by examples of graphical shapes and their corresponding derivatives.

10:01

🧮 Analyzing a Cubic Function

This paragraph presents a step-by-step analysis of a cubic function, focusing on finding intervals of increase and decrease, critical numbers, local extrema, and inflection points. The process begins with finding the first derivative and setting it to zero to find critical numbers. A sign chart is used to determine where the function is increasing or decreasing and to identify local maximum and minimum values. The second derivative test is then applied to find concavity and inflection points, with the paragraph concluding with a graphical representation of the function's behavior.

15:01

📉 Examining a Composite Function

The fourth paragraph continues the analysis with a composite function, emphasizing the use of the chain rule to find the first derivative. Critical numbers are determined by setting the first derivative equal to zero and factoring. The paragraph discusses the sign changes of the first derivative to identify intervals of increase and decrease, as well as local minimum and maximum values. The second derivative is then found to determine concavity and inflection points, with the function's behavior summarized in a table and graphed for visual understanding.

20:04

🔢 Solving a Radical Function

In this paragraph, the focus is on a radical function, where the product rule is used to find the first derivative. The critical numbers are found by setting the numerator and denominator of the derivative equal to zero. The domain of the function is discussed due to the square root, and the sign of the first derivative is analyzed to determine intervals of increase and decrease, as well as local minimum and maximum values. The second derivative is then calculated using the quotient rule, leading to the identification of concavity and inflection points. The paragraph concludes with a discussion on the function's behavior and its graph.

25:08

📈 Investigating a Power Function

The final paragraph examines a power function, detailing the process of finding the first and second derivatives. The sign of the first derivative is used to identify intervals where the function is increasing and decreasing, and to find local minimum and maximum values. The second derivative is then used to determine the function's concavity and inflection points. The paragraph concludes with a comprehensive summary of the function's behavior across its domain, highlighting key points such as the presence of a cusp and the function's continuity and differentiability at zero.

Mindmap

Keywords

💡First Derivative

The first derivative of a function represents the slope of the function at any given point. In the context of the video, it is used to determine whether a function is increasing (positive first derivative) or decreasing (negative first derivative). For instance, when the first derivative is zero, it indicates a potential local maximum or minimum, as seen when discussing critical points and inflection points.

💡Second Derivative

The second derivative of a function is the derivative of the first derivative and indicates how the slope of the function is changing. A positive second derivative means the function is concave up, while a negative second derivative means the function is concave down. In the video, the second derivative is used to identify inflection points, where the concavity of the function changes from concave up to concave down or vice versa.

💡Critical Points

Critical points are points on the graph of a function where the first derivative is either zero or undefined. These points are significant because they often represent local maximum or minimum values or points of inflection. In the video, the process of finding critical points involves setting the first derivative equal to zero and solving for the variable.

💡Local Maximum/Minimum

Local maximum and minimum values on a function are points where the function reaches a peak or a trough within a certain interval. These points are identified by a change in the sign of the first derivative from positive to negative for a local maximum and from negative to positive for a local minimum.

💡Inflection Points

Inflection points are points on a graph where the concavity of the function changes. This means the function goes from being concave up to concave down or vice versa at these points. Inflection points are important in understanding the shape of a function's graph and are found when the second derivative is zero or changes sign.

💡Concavity

Concavity refers to the curvature of a function's graph. A function is said to be concave up when its graph curves upwards like a U, and concave down when it curves downwards. The concavity is determined by the sign of the second derivative, with a positive second derivative indicating concavity up and a negative second derivative indicating concavity down.

💡Sign Chart

A sign chart is a tool used in calculus to determine the sign of a function's first derivative at different intervals. By testing values within these intervals, one can determine where the function is increasing or decreasing and can identify intervals of increase and decrease, as well as critical points.

💡Chain Rule

The chain rule is a technique in calculus used to find the derivative of a composite function. It involves differentiating the outer function and then multiplying by the derivative of the inner function. The chain rule is essential for dealing with complex functions that involve other functions.

💡Product Rule

The product rule is a fundamental calculus rule used to find the derivative of a product of two functions. According to the product rule, the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function.

💡Quotient Rule

The quotient rule is a calculus rule used to find the derivative of a quotient of two functions. The rule states that the derivative of a quotient is the derivative of the numerator times the denominator minus the numerator times the derivative of the denominator, all divided by the denominator squared.

💡Domain

The domain of a function is the set of all possible input values (x-values) for which the function is defined. The domain is important because it specifies the range of values over which the function can be accurately evaluated without resulting in undefined expressions or discontinuities.

Highlights

The video focuses on understanding the behavior of functions in terms of intervals, concavity, and critical points.

A function is increasing when its first derivative is positive and decreasing when the first derivative is negative.

The first derivative being zero indicates a constant function or a horizontal tangent line at a particular point.

Local maximum and minimum values can be identified by changes in the sign of the first derivative.

Critical points occur where the first derivative is zero or does not exist, indicating potential local extrema.

A function is concave up when the second derivative is positive, indicating that the first derivative is increasing.

Conversely, a function is concave down when the second derivative is negative, meaning the first derivative is decreasing.

Inflection points are identified when the concavity changes, i.e., the second derivative crosses zero and the sign changes.

The video provides a detailed analysis of a function's behavior using the first and second derivatives.

The process of finding critical numbers and inflection points is demonstrated through examples.

The video explains how the sign of the first derivative changes at local maximum and minimum points.

The concept of concavity and inflection points is clarified with graphical representations.

The video uses the first derivative test to determine local maxima and minima.

The second derivative test is used to classify intervals as concave up or concave down.

The video provides a comprehensive guide to understanding the relationship between derivatives and the shape of a function's graph.

The process of finding the domain and analyzing the function's behavior at critical points is discussed.

The video concludes with a summary of the key concepts and a thank you message to the viewers.

Transcripts

Browse More Related Video

Calculus AB Homework 4.5: Second Derivative Test

What the Second Derivative Tells Us

3.2 - Using Second Derivatives to Classify Max and Min Values

Business Calculus - Math 1329 - Section 3.2 - Concavity and Points of Inflection

Calculus AB Homework 4.6: Relationship between f, f', and f''

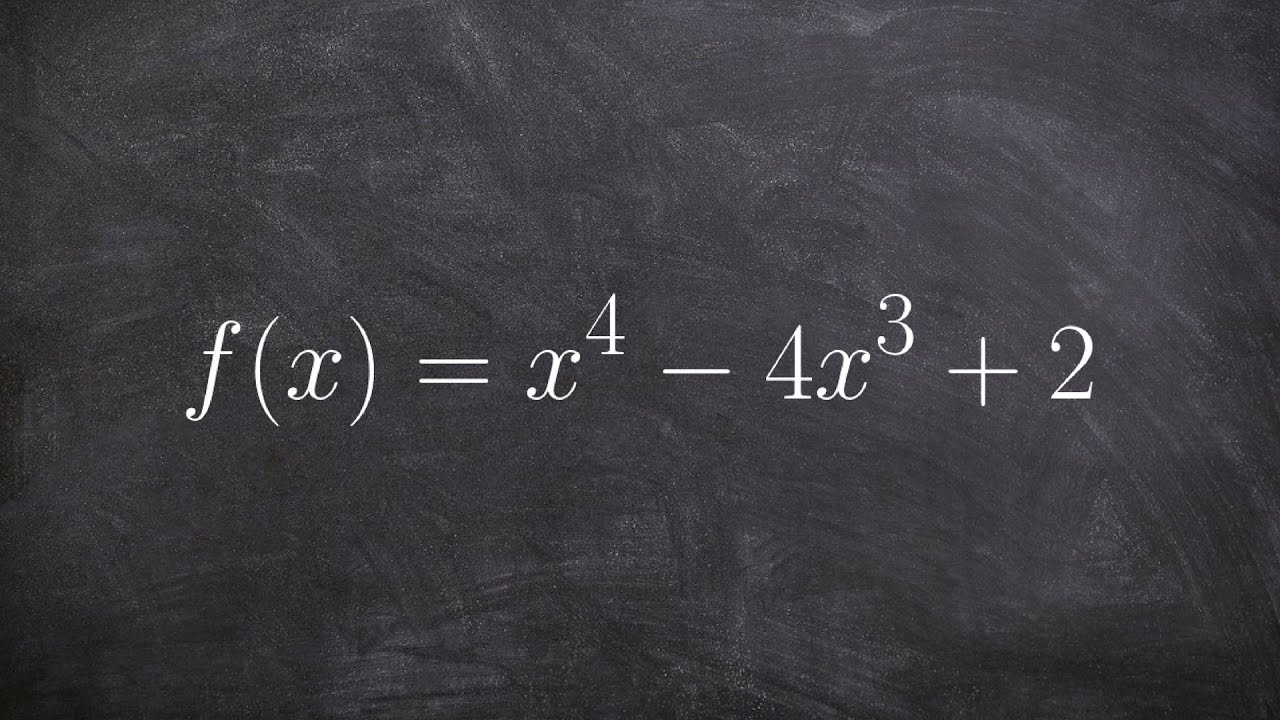
Learn how to determine concavity and point of inflection AP style

Related Tags

Calculus Tutorial Function Analysis First Derivative Second Derivative Increasing Decreasing Concave Up Down Local Extrema Inflection Points Critical Numbers Math Education