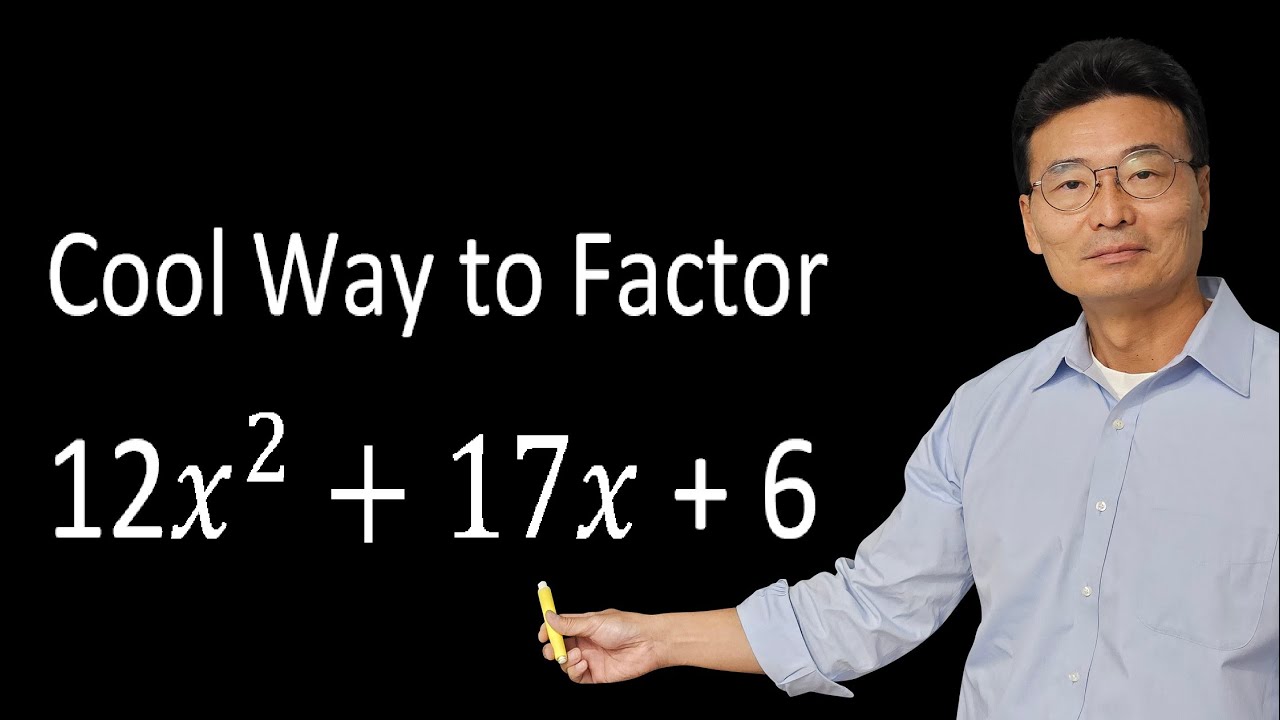Box Method of Factoring Trinomials (10 Examples)
TLDRThis instructional video script introduces the box method for factoring trinomials, a technique that simplifies algebra for students. It walks through the process of identifying two numbers that multiply to the product of the leading coefficient and constant term, while also adding up to the middle coefficient. The script provides ten examples to illustrate the method, emphasizing the importance of finding the greatest common factor and practicing the steps to master factoring. It also encourages viewers to pause and attempt examples independently for better understanding.
Takeaways
- 📚 The video teaches how to factor trinomials using the box method, which simplifies the process for students learning algebra.
- 📉 The box method involves identifying two numbers that multiply to the product of the leading coefficient and the constant term, and add up to the middle coefficient.
- 🔍 Students are encouraged to pause the video and try examples on their own to gain more practice in factoring trinomials.
- 📝 The process includes placing the leading term and constant term in respective corners and the two identified numbers in the middle boxes.
- 🔢 Examples demonstrate how to find the greatest common factor (GCF) in each row and factor it out to simplify the expression.
- 📉 The video provides a step-by-step guide through multiple examples, showing the application of the box method in different scenarios.
- 🔄 The importance of checking work by using the FOIL method or distribution to ensure the factored form is correct is emphasized.
- 📈 For larger numbers, the script suggests using a prime factorization tree method to find the correct pair of numbers for the box method.
- 📝 The script also covers cases where the leading coefficient is understood to be one, and how to adjust the method accordingly.
- 🔑 The video mentions additional resources for learning more about factoring, including other methods and video courses for further study.
- 🎓 The presenter offers support for viewers through video courses, Patreon memberships, and merchandise, showing multiple ways to engage with the content.
Q & A
What is the main topic of the video?
-The main topic of the video is teaching students how to factor trinomials using the box method in algebra.
What is the purpose of the box method in factoring trinomials?
-The purpose of the box method is to simplify the process of factoring trinomials, making it easier for students to understand and apply.
How many examples are provided in the video to demonstrate the box method?
-The video provides 10 examples to demonstrate the box method for factoring trinomials.
What is the first step in the box method for factoring trinomials?
-The first step is to multiply the leading coefficient (a) by the constant term (C) to find the product a times C.
What are the two criteria for the two numbers that are found in the box method?
-The two numbers must multiply to the product of the leading coefficient and the constant term (a times C) and add up to the middle coefficient (B).
What is the significance of the greatest common factor (GCF) in the box method?
-The greatest common factor is used to simplify each row of the box by factoring it out, which helps in breaking down the trinomial into its factored form.
How does the video suggest checking the work after factoring a trinomial?
-The video suggests checking the work by using the FOIL method or distributing twice to ensure that the factored form results in the original trinomial.
What is the strategy for finding the two numbers that meet the criteria in the box method?
-The strategy involves listing pairs of factors of the product a times C and checking which pair adds up to the middle coefficient B.
What is the importance of considering the sign of the constant term when placing it in the box?
-The sign of the constant term is important because it determines whether the factors in the box should be positive or negative to satisfy the addition criterion for the middle coefficient B.
How does the video handle the case when the leading coefficient is not explicitly stated in the trinomial?
-When the leading coefficient is not stated, it is understood to be 1, and the process continues with this implicit value.
What is the 'prime factorization tree' method mentioned in the video for dealing with larger numbers?
-The 'prime factorization tree' method involves breaking down the numbers into their prime factors and then using these factors to find two numbers that meet the multiplication and addition criteria for the box method.
How does the video suggest students practice the box method?
-The video suggests pausing the video and trying the examples on their own to get more practice with the box method.
What additional resources are mentioned in the video for further learning on factoring?
-The video mentions other videos on 'Learn How to Factor', 'Learn Algebra 1', and 'Learn Algebra 2/College Algebra' video courses for sale, as well as a YouTube channel named 'Myers Matthew' for more factoring techniques.
Outlines
📚 Introduction to the Box Method for Factoring Trinomials
This paragraph introduces the video's focus on teaching the box method for factoring trinomials, a technique that simplifies the process for students. The script mentions that viewers might want to pause and practice along with the 10 examples provided. The method involves identifying two numbers that multiply to the product of the leading coefficient and the constant term while also adding up to the middle coefficient. The process is illustrated with a sample problem involving a trinomial with a leading coefficient of 3, a middle coefficient of -2, and a constant term of -8, showing how to apply the box method to factor it into (3x - 4)(x + 2).
🔍 Detailed Explanation of the Box Method with Examples
The paragraph delves deeper into the box method with additional examples. It explains how to find two numbers that meet specific multiplication and addition criteria, and then how to apply these numbers to factor the trinomial. The script walks through the process of factoring a trinomial with coefficients 6, -17, and 42, identifying the correct pair of numbers (-14 and -3) that satisfy the conditions. The paragraph also emphasizes the importance of factoring out the greatest common factor before applying the box method and provides a step-by-step guide to factoring another trinomial with coefficients 1, -1, and -12 into (x - 4)(x + 3).
📘 Factoring Trinomials with Higher Degree Terms
This section of the script addresses how to factor trinomials that include higher degree terms, such as x squared. The process involves identifying the correct pair of numbers that multiply to the product of the leading coefficient (implicitly 1 if not shown) and the constant term, while also adding to the middle coefficient. The script provides an example of factoring x squared - x - 12 into (x - 4)(x + 3) by finding the numbers -4 and 3 that meet the criteria. It also discusses the use of prime factorization to assist in finding the correct pair of numbers for more complex trinomials.
📝 Further Practice and Additional Resources for Factoring
The paragraph encourages viewers to practice factoring on their own and provides a brief overview of additional resources available for learning algebra. It mentions the availability of video courses for Algebra 1 and Algebra 2/College Algebra, which cover a full curriculum in a step-by-step manner. The script also invites viewers to support the channel through membership or by purchasing t-shirts from the Teespring store, with links provided in the video description. The focus then shifts to more examples of factoring, including a trinomial with coefficients 8, 21, and 10, which is factored into (8x + 5)(x + 2).
📌 Applying the Box Method to More Complex Trinomials
This paragraph continues the application of the box method to factor more complex trinomials, including those with larger coefficients and negative terms. The script demonstrates the process with a trinomial that has coefficients 9, -30, and 225, factored into (3x - 15)(3x + 15). It also addresses the importance of recognizing the correct signs and using the prime factorization tree method to assist in finding the appropriate pair of numbers for the factoring process.
📚 Final Examples and Encouragement to Continue Learning
The final paragraph wraps up the video with a few more examples of factoring trinomials using the box method. It provides a brief analysis of each example, including identifying the correct pair of numbers that meet the multiplication and addition criteria. The script encourages viewers to continue practicing and learning about factoring through the provided resources. It also invites viewers to watch another video on 'Learn How to Factor' for more techniques and examples, signaling the end of the current instructional video.
Mindmap
Keywords
💡Factoring
💡Trinomial
💡Box Method
💡Leading Coefficient
💡Constant
💡Middle Coefficient
💡Greatest Common Factor (GCF)
💡Foil Method
💡Prime Factorization
💡Variable
💡Commutative Property
Highlights
Introduction to the Box Method for factoring trinomials, a technique to simplify algebra for students.
Explanation of the basic concept of the Box Method involving a trinomial with three terms.
Guidance on multiplying the leading coefficient by the constant to find two numbers that meet specific criteria.
Demonstration of placing terms in a box and identifying the correct pair of numbers that fulfill the equation's requirements.
Step-by-step walkthrough of the first example using the Box Method with a trinomial equation.
Emphasis on finding the greatest common factor (GCF) as the initial step in the factoring process.
Illustration of factoring out the GCF from each row in the Box Method to simplify the equation.
Introduction of the second example showcasing the process of identifying two numbers that meet specific multiplication and addition criteria.
Discussion on the importance of recognizing the signs of the numbers when factoring trinomials.
Presentation of a third example with a variable squared term and the process of identifying the correct pair of numbers.
Explanation of the use of prime factorization to assist in finding the correct pair of numbers for larger coefficients.
Introduction of the fourth example with a larger coefficient and the method of breaking down the number into prime factors.
Demonstration of the process for the fifth example, emphasizing the use of prime factorization for complex numbers.
Explanation of the sixth example, focusing on the method of identifying two numbers that add up to a negative coefficient.
Introduction of the seventh and eighth examples, encouraging viewers to practice the Box Method on their own.
Discussion on the use of the Box Method for equations with negative coefficients and the importance of factoring out negative numbers.
Presentation of the ninth and tenth examples, highlighting the application of the Box Method in various scenarios.
Final summary of the Box Method, encouraging viewers to practice and explore other factoring techniques.
Promotion of additional learning resources, including video courses and merchandise, for further support and practice.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: