Margin of error 1 | Inferential statistics | Probability and Statistics | Khan Academy

Khan Academy
29 Oct 201015:02
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses a hypothetical scenario of a presidential election in a country with 100 million people, where voters choose between two candidates, A and B. It uses a Bernoulli Distribution to model the voting behavior, where voting for A is represented by 0 and for B by 1. The mean of this distribution is p, the probability of voting for B. Due to the impracticality of surveying the entire population, a random sample of 100 people is taken to estimate p. The sample mean and variance are calculated, leading to an estimated p of 43% for candidate B. The script then explores the concept of sample standard deviation and introduces the idea of constructing a confidence interval to gauge the accuracy of the sample in representing the entire population's voting intentions.

Takeaways
  • 🗳️ The script discusses a hypothetical presidential election scenario in a country with 100 million people and two candidates, A and B.
  • 📊 It introduces the concept of a Bernoulli Distribution to model the binary outcome of voting for either candidate A (0) or candidate B (1).
  • 🧐 The mean of the Bernoulli Distribution is established as 'p', representing the probability that a randomly selected individual will vote for candidate B.
  • 🔍 Due to the impracticality of surveying 100 million people, the script suggests estimating 'p' through a random sample of the population.
  • 🔢 A sample of 100 people is taken, with 57 indicating they would vote for A and 43 for B, leading to a sample mean calculation of 0.43.
  • 📐 The sample variance is calculated using the formula, resulting in an estimate of 0.2475, which is then used to estimate the population variance.
  • 📏 The sample standard deviation is derived from the square root of the sample variance, estimated to be approximately 0.50.
  • 🌐 The script discusses the concept of the sampling distribution of the sample mean and its properties, such as its mean and standard deviation.
  • 🔄 An estimate for the standard deviation of the sampling distribution of the sample mean is calculated using the sample standard deviation divided by the square root of the sample size.
  • 📉 The script highlights the uncertainty in estimating the true population mean and variance, emphasizing that these are estimates based on the sample.
  • 📚 The final part of the script teases the calculation of a confidence interval, suggesting that the next video will cover how to estimate the range within which the true population mean is likely to fall with a certain level of confidence.
Q & A

  • What is the context of the presidential election scenario described in the script?

    -The context is a hypothetical scenario where there are two candidates in a presidential election, and the population is 100 million. Every eligible voter will cast a vote for either candidate A or candidate B.

  • What is the significance of the variable 'p' in this scenario?

    -The variable 'p' represents the percentage of the population that is expected to vote for candidate B. It is a key parameter in the Bernoulli distribution used to model the voting outcomes.

  • Why is it not feasible to survey all 100 million people?

    -It is practically impossible to survey all 100 million people due to the sheer size of the population and the resources required for such a large-scale survey.

  • What is the purpose of conducting a random survey in this scenario?

    -The purpose of conducting a random survey is to estimate the value of 'p', which represents the proportion of the population that will vote for candidate B.

  • How many people are sampled in the random survey described in the script?

    -In the script, a random survey of 100 people is conducted to estimate the voting preferences.

  • What is the sample mean calculated from the survey results?

    -The sample mean is calculated as 0.43, which is derived from 57 people voting for candidate A (0s) and 43 people voting for candidate B (1s), divided by the total number of samples (100).

  • What is the sample variance calculated from the survey results?

    -The sample variance is calculated to be 0.2475, which is determined by the squared distances of each sample from the mean, divided by the number of samples minus one (99).

  • How is the sample standard deviation related to the sample variance?

    -The sample standard deviation is the square root of the sample variance. In this case, it is approximately 0.50 or 50%.

  • What is the concept of a sampling distribution of the sample mean?

    -The sampling distribution of the sample mean is the distribution that would result if we were to take many samples from the population and calculate the mean of each sample. It helps us understand the variability of sample means.

  • Why is the standard deviation of the sampling distribution of the sample mean divided by the square root of the sample size?

    -The division by the square root of the sample size is a mathematical property that relates the standard deviation of the population to the standard deviation of the sample means, reflecting the reduction in variability as sample size increases.

  • How can we estimate the standard deviation of the population from the sample?

    -We can estimate the standard deviation of the population by using the sample standard deviation as our best estimate and then dividing it by the square root of the sample size.

  • What is the purpose of finding a confidence interval for the sample mean?

    -The purpose of finding a confidence interval is to provide a range around the sample mean within which we can be reasonably confident (e.g., 95% sure) that the true population mean lies.

  • How does the estimated standard deviation of the sampling distribution of the sample mean affect the width of the confidence interval?

    -A smaller estimated standard deviation will result in a narrower confidence interval, indicating greater precision in our estimate. Conversely, a larger standard deviation will result in a wider interval.

Outlines
00:00
🗳️ Presidential Election and Bernoulli Distribution

The script begins with a hypothetical scenario set in a country of 100 million people with an upcoming presidential election featuring two candidates, A and B. The narrator introduces the concept of a Bernoulli Distribution to model the binary outcome of voters choosing either candidate A (represented as 0) or candidate B (represented as 1). The mean of this distribution is highlighted as 'p', which represents the probability that a voter will choose candidate B. The challenge of determining the exact value of 'p' is discussed, as it would require surveying the entire population, which is impractical. Instead, the narrator proposes using a random sample to estimate 'p' and assess the quality of this estimate.

05:01
📊 Calculating Sample Mean and Variance

This paragraph delves into the specifics of conducting a random survey and calculating the sample mean and variance based on the responses. The narrator provides an example where 57 out of 100 surveyed individuals indicate they would vote for candidate A, and 43 for candidate B. The sample mean is calculated by taking the average of the 0's (for A) and 1's (for B), resulting in 0.43. The sample variance is then computed using the formula that involves the squared distances of each sample point from the mean, divided by the sample size minus one, yielding a variance of 0.2475. The sample standard deviation is derived from the variance, which is approximately 0.50. The narrator emphasizes the importance of these statistics in estimating the true population parameters.

10:01
📉 Estimating Confidence Intervals for Population Proportion

The final paragraph focuses on the concept of confidence intervals and how they can be used to estimate the true population mean (or proportion of votes for candidate B) with a certain level of confidence. The narrator explains that the sampling distribution of the sample mean is derived from the population distribution and that its mean (mu sub x-bar) is equal to the population mean (mu), which is 'p'. The standard deviation of the sampling distribution is calculated by dividing the population standard deviation by the square root of the sample size. Since the true population standard deviation is unknown, the sample standard deviation is used as an estimate. The narrator then discusses the process of creating a confidence interval around the sample mean, using the estimated standard deviation and a 95% confidence level, to assert that there is a high probability that the true population mean lies within this interval. The video concludes with a pause for reflection on the concepts covered and a teaser for the next video, which will continue the discussion on confidence intervals.

Mindmap
Keywords
💡Presidential Election
A presidential election is a democratic process where citizens vote to elect their president. In the context of the video, it serves as the backdrop for discussing statistical concepts. The script uses a hypothetical election with two candidates, A and B, to illustrate how statistical sampling and distributions can be applied to real-world scenarios.
💡Candidates A and B
In the script, 'Candidates A and B' represent the two individuals running for president in the hypothetical election. They are used as a simplified model to discuss the Bernoulli Distribution, where each citizen's vote is treated as a binary outcome (0 for Candidate A, 1 for Candidate B).
💡Bernoulli Distribution
A Bernoulli Distribution is a discrete probability distribution for a random variable that takes the value 1 with probability p and the value 0 with probability 1-p. In the video, it is used to model the binary outcome of voting for either Candidate A or B, with p representing the probability of voting for Candidate B.
💡Mean
The mean, often referred to as the average, is a measure of central tendency in statistics. In the context of the video, the mean of the Bernoulli Distribution is equated to p, which is the probability of voting for Candidate B. The script explains that the mean of the sampling distribution of the sample mean is also equal to p.
💡Sample
A sample is a subset of a population that is used to represent the population for statistical analysis. In the script, the speaker conducts a random survey of 100 people to estimate the value of p, which is not feasible to determine by asking all 100 million citizens.
💡Sample Mean
The sample mean is the average of the values within a sample. In the video, the speaker calculates the sample mean by adding the number of votes for Candidate A (0's) and Candidate B (1's) and dividing by the total number of samples (100), resulting in a sample mean of 0.43.
💡Sample Variance
Sample variance is a measure that quantifies the degree of variation or dispersion in a set of data points in a sample. The script describes how to calculate it by taking the sum of the squared differences between each sample point and the sample mean, divided by the sample size minus one (n-1), resulting in a sample variance of 0.2475.
💡Sample Standard Deviation
The sample standard deviation is the square root of the sample variance and provides a measure of the amount of variation or dispersion of sample data points in the sample. The script calculates it as the square root of the sample variance, resulting in a sample standard deviation of approximately 0.50.
💡Confidence Interval
A confidence interval is a range of values, derived from a statistical model, that is likely to contain the value of an unknown parameter. The script discusses creating a confidence interval around the sample mean to estimate the true population mean (p) with a certain level of confidence, in this case, 95%.
💡Sampling Distribution
The sampling distribution is the probability distribution of a given statistic based on a random sample. The video explains that the sampling distribution of the sample mean is used to estimate the population mean and that its standard deviation is the population standard deviation divided by the square root of the sample size.
Highlights

A presidential election scenario with two candidates is presented to illustrate a Bernoulli Distribution.

The concept of p percent voting for candidate B and (1-p) percent for candidate A is introduced.

The mean of the Bernoulli Distribution is established as being equal to p.

The challenge of estimating the true mean (p) in a population of 100 million without surveying everyone is discussed.

A random survey of 100 people is proposed as a method to estimate p.

The results of the survey, with 57 voting for candidate A and 43 for candidate B, are given.

Calculation of the sample mean, resulting in 0.43, is demonstrated.

The process of calculating the sample variance is explained, with a focus on squared distances from the mean.

The sample variance is calculated to be 0.2475, using the formula and a calculator.

The sample standard deviation is derived as the square root of the sample variance, approximately 0.50.

The importance of the sample mean as an estimate for the percentage of people voting for each candidate is emphasized.

The concept of a confidence interval is introduced to gauge the accuracy of the sample as an estimator.

The standard deviation of the sampling distribution of the sample mean is discussed, highlighting its dependence on the population standard deviation and sample size.

An estimate for the standard deviation of the sampling distribution is calculated using the sample standard deviation.

The video pauses to prompt viewers to consider how to find a 95% confidence interval based on the information provided.

The video concludes with a teaser for the next part, which will cover calculating the confidence interval.

Transcripts

Browse More Related Video

Confidence interval example | Inferential statistics | Probability and Statistics | Khan Academy

Sample standard deviation and bias | Probability and Statistics | Khan Academy

Sample variance | Descriptive statistics | Probability and Statistics | Khan Academy

Introduction to sampling distributions | Sampling distributions | AP Statistics | Khan Academy

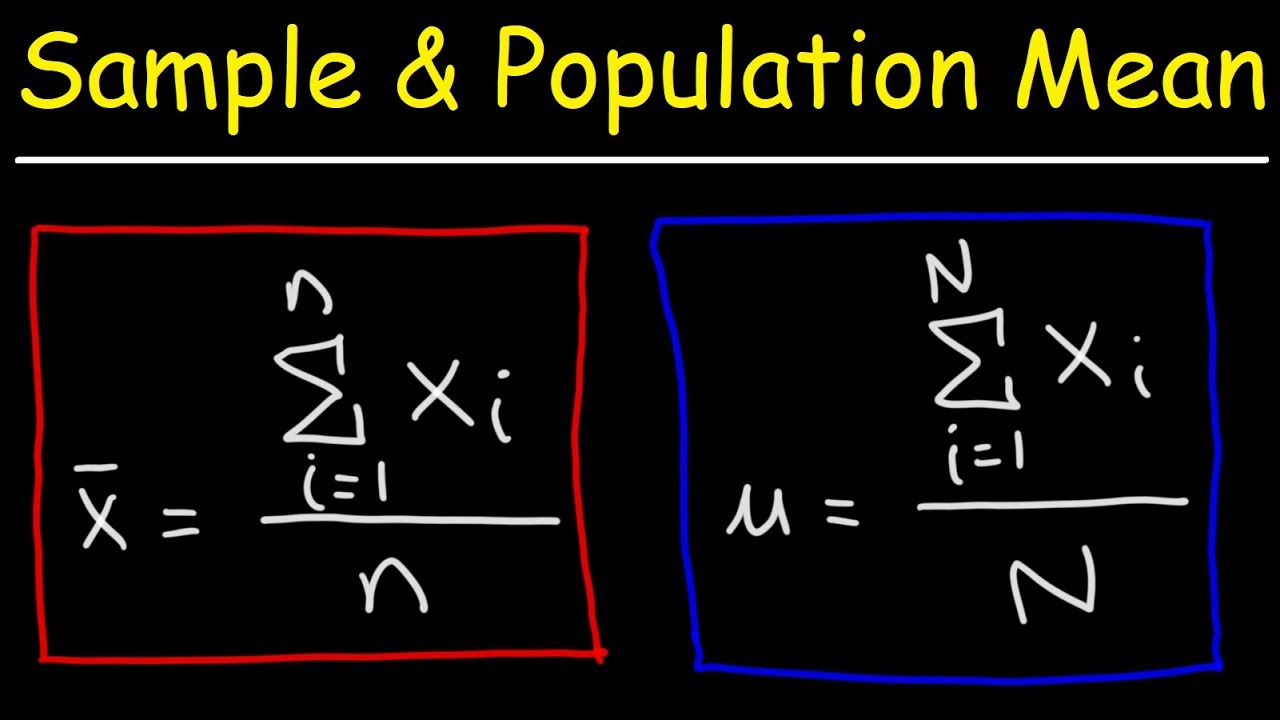
Sample Mean and Population Mean - Statistics

Confidence Interval for a population proportion | Solved Problems

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Election AnalysisSampling MethodConfidence IntervalStatistical EstimationBernoulli DistributionPopulation SurveyData InterpretationVoting BehaviorSample VarianceStandard Deviation