Sample Mean and Population Mean - Statistics

The Organic Chemistry Tutor
24 Jan 201905:04
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains the difference between a sample and a population, using a city of 100,000 people as an example of a population. A sample of 100 people is used to estimate characteristics of the overall population, like the average weight. The sample mean calculates the average of the sample while the population mean calculates the average of the entire population. Increasing the sample size improves the estimate of the population mean. The sample mean is a statistic while the population mean is a parameter. Formulas are provided for calculating the sample mean and population mean, which differ only in using n for the sample size and N for the total population size.

Takeaways
  • ๐Ÿ˜€ The population refers to the entire group we want to study, while the sample is a subset of the population we measure.
  • ๐Ÿ‘ฅ We take a sample because it's impractical to measure an entire population.
  • ๐Ÿ“Š The sample mean (x-bar) is the sum of the sample data values divided by the sample size (n).
  • ๐Ÿ“ˆ The population mean (ฮผ) is the sum of all the population data values divided by the total population size (N).
  • ๐ŸŽฏ We want the sample mean to best estimate the population mean. Increasing the sample size helps it approach the actual population mean.
  • i The sample mean is a statistic - a measure of a sample. The population mean is a parameter - a measure of a population.
  • ๐Ÿงฎ The formula for sample mean sums the sample data values from x1 to xn, divided by sample size n.
  • ๐Ÿงฎ The formula for population mean sums the population data values from x1 to xN, divided by population size N.
  • ๐Ÿ”ข Sample size (n) and population size (N) are key components of these formulas.
  • ๐Ÿ“ In summary, the sample mean estimates the population mean. Increasing sample size improves this estimate.
Q & A

  • What is the difference between a sample and a population?

    -A population refers to the entire group you want to study or make conclusions about. A sample is a subset of the population that is used to estimate characteristics of the whole population.

  • How is the sample mean calculated?

    -The sample mean is calculated by summing all the observed values in the sample and dividing by the number of items in the sample (n). The formula is ฮฃx/n.

  • What is the formula for calculating the population mean?

    -The formula for the population mean is ฮฃx/N, where N represents the number of individuals in the entire population.

  • Why is it impractical to measure the entire population in this example?

    -In this example, the population size is 100,000 people. Attempting to measure the weight of 100,000 people would require significant time and resources, so a sample is used instead to estimate the average weight.

  • What is the trade-off between sample size and accuracy?

    -Larger sample sizes lead to more accurate estimates of the population mean, but require more effort and resources to collect data. Smaller samples are easier to obtain but may be less precise.

  • What terms are used to refer to the sample mean and the population mean?

    -The sample mean is referred to as a statistic. The population mean is referred to as a parameter.

  • As sample size increases, how does the sample mean change relative to the population mean?

    -As the sample size increases, the sample mean approaches and gets closer to the actual population mean.

  • What Greek letter represents the population mean?

    -The Greek letter mu (ฮผ) represents the population mean.

  • What notation is used to represent summing values in statistics formulas?

    -Sigma (ฮฃ) notation is used to represent summing values in statistical formulas.

  • What are some examples of statistics that describe a sample?

    -Examples of sample statistics include the sample mean, sample median, sample mode, and sample standard deviation.

Outlines
00:00
๐Ÿ˜€ Defining Sample vs Population

The first paragraph defines the key difference between a sample and a population. A population refers to the entire group we want to study - it could be all the people living in a city. A sample is a subset of that population that we actually collect data from. For example, we may survey 100 people out of a city of 100,000 to estimate characteristics about the overall city population.

๐Ÿ˜ƒ Calculating Sample and Population Means

The second paragraph explains how to calculate the sample mean versus the population mean. The sample mean takes the sum of the sample data values divided by the sample size n. The population mean takes the sum of all the population data values divided by the total population size N. We want the sample mean to approximate the population mean. Increasing the sample size n makes the sample mean approach the actual population mean more closely.

๐Ÿ˜Š Sample Mean vs Population Parameter

The third paragraph distinguishes between a sample statistic like the sample mean, versus a population parameter like the population mean. The sample mean is considered a statistic, while the population mean is a parameter. Other examples of statistics are median, mode, etc. calculated on a sample, while parameters describe the overall population.

๐Ÿ“ Formulas for Sample and Population Means

The fourth paragraph presents the mathematical formulas for calculating the sample mean and population mean. The formulas sum up the sample or population data values respectively and divide by the sample size n or total population size N. The formulas look very similar, differing only in using lowercase n versus uppercase N to represent if it is a sample or population calculation.

Mindmap
Keywords
๐Ÿ’กsample
A sample represents a subset or portion of the larger population. In the context of the video, a sample refers to a small group of 100 people selected from the larger population of 100,000 people living in the city. Sampling is necessary because it is not practical to gather data from the entire population. The sample mean calculated from the sample can be used to estimate the population mean.
๐Ÿ’กpopulation
The population refers to the entire group that is being studied or analyzed. In this case, the population is all 100,000 citizens living in the city. The population mean (mu) provides the actual average for the entire population, but is often not feasible to calculate directly.
๐Ÿ’กsample mean
The sample mean, represented by x-bar, is the sum of all the sample data values divided by the sample size (n). It provides an estimate of the population mean based on the sample data. As the sample size increases, the sample mean approaches the actual population mean.
๐Ÿ’กpopulation mean
The population mean, represented by mu, is the sum of all the population data values divided by the population size (N). It gives the exact average for the entire target population group.
๐Ÿ’กstatistic
A statistic is a quantity calculated from sample data, such as the mean, median, or mode. The sample mean is considered a statistic because it is computed from a sample. Statistics provide estimates of population parameters.
๐Ÿ’กparameter
A parameter refers to a quantity describing the population, not the sample. The population mean is considered a parameter because it represents an actual fact about the population. Parameters are fixed values that statistics attempt to estimate.
๐Ÿ’กformulas
The video explains the formulas for calculating both the sample mean (x-bar) and population mean (mu). The formulas are very similar except for using n and N to represent sample and population sizes, respectively.
๐Ÿ’กaccuracy
Larger sample sizes increase accuracy - that is, make the sample mean closer to the actual population mean. But larger samples require more effort to collect data. So there is a tradeoff between accuracy and feasibility.
๐Ÿ’กestimate
The sample mean provides an estimate of the unknown population mean. As an estimate from a subset, it will contain some error, but can still be useful for drawing conclusions about the real average.
๐Ÿ’กapproach
As the sample size grows, the sample mean approaches the population mean. This indicates the estimate steadily improves and gets closer to the actual parameter value.
Highlights

The population refers to the entire group we want to study

A sample is a subset of the population that is used to estimate characteristics of the whole population

The sample mean is calculated by summing the sample data values and dividing by the sample size n

The population mean sums data values of the entire population and divides by population size N

The sample mean is a statistic - a measure of the sample

The population mean is a parameter - a measure of the population

Increasing the sample size improves the estimate of the population mean

Larger sample size requires more effort to collect data

Sample mean formula sums the sample data values from x1 to xn, divided by sample size n

Population mean formula is similar but sums values for entire population from x1 to xN, divided by N

Lowercase n represents sample size

Capital N represents population size

Sample mean is calculated by summing sample data values and dividing by sample size n

Population mean formula sums all population data values and divides by population size N

Sample mean uses lowercase n for sample size

Population mean uses capital N for total population size

Formulas for sample and population mean are similar with only difference being sample size n vs. population size N

Now you know formulas for calculating sample mean and population mean

Transcripts

Browse More Related Video

Population Mean And Sample Mean (Explanation and Walkthrough Example) |Statistics

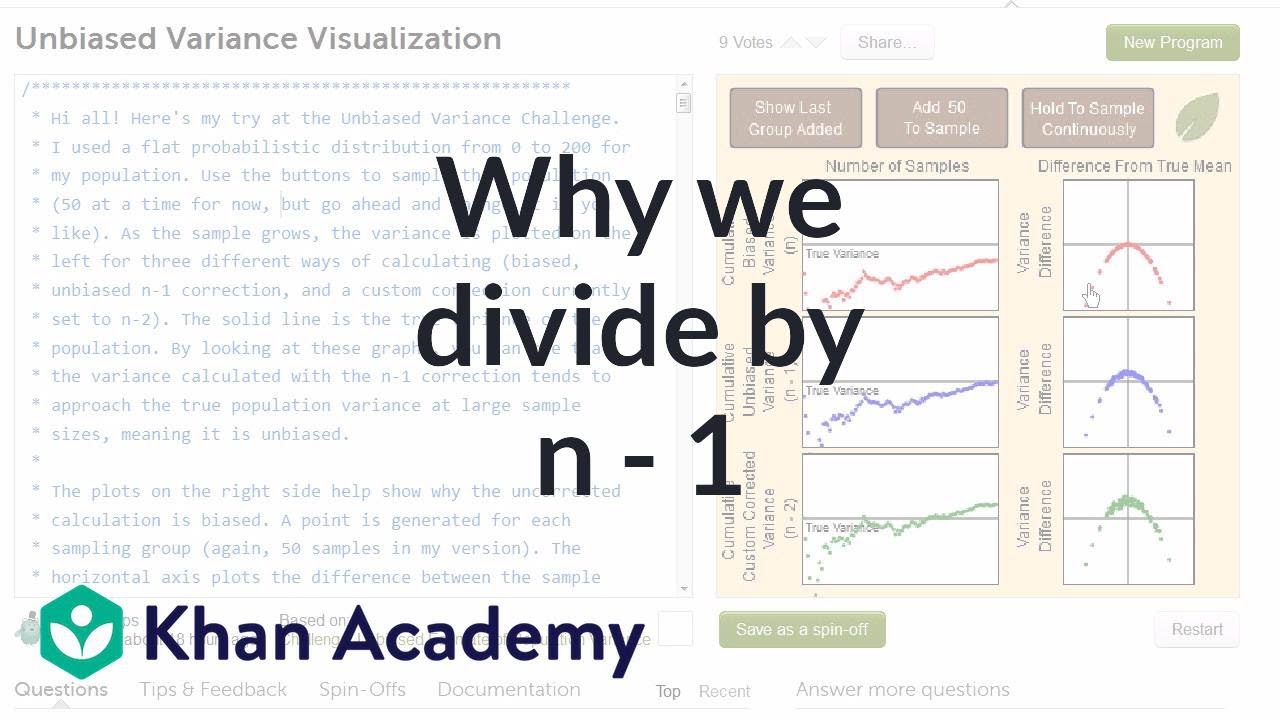
Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance

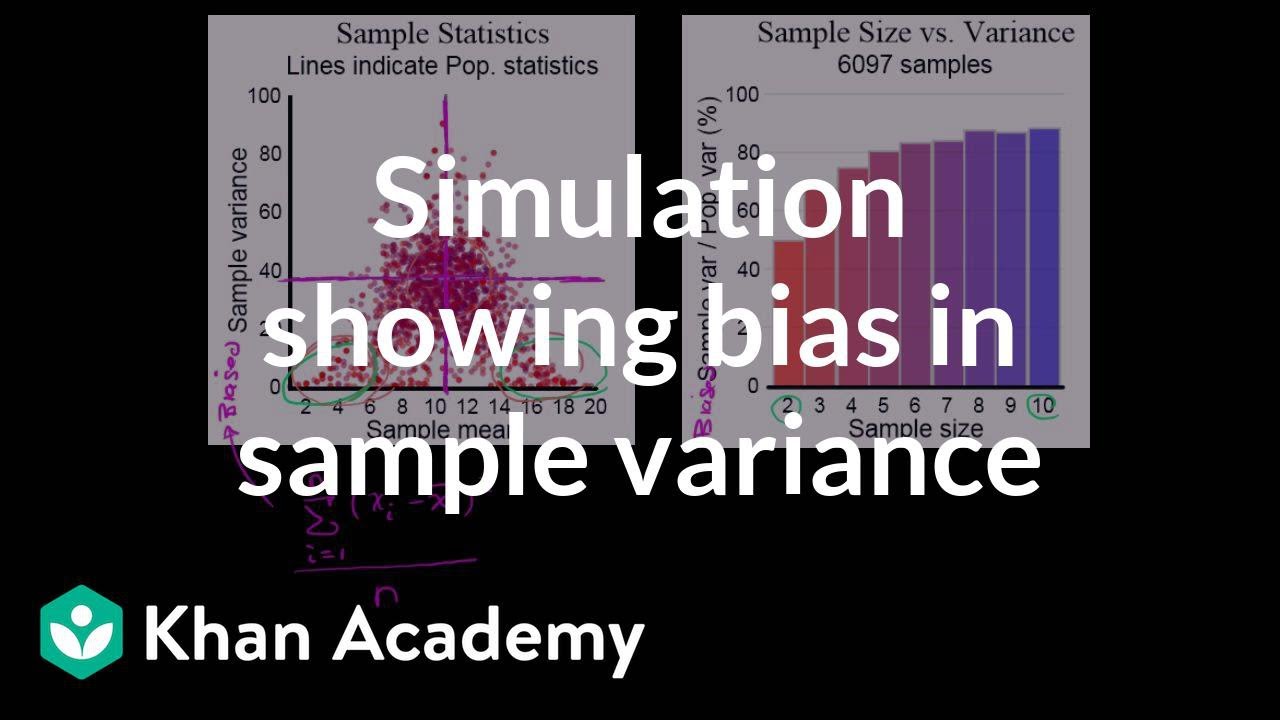
Simulation showing bias in sample variance | Probability and Statistics | Khan Academy

How to Calculate Population Mean (Parameter and Examples) | Statistics

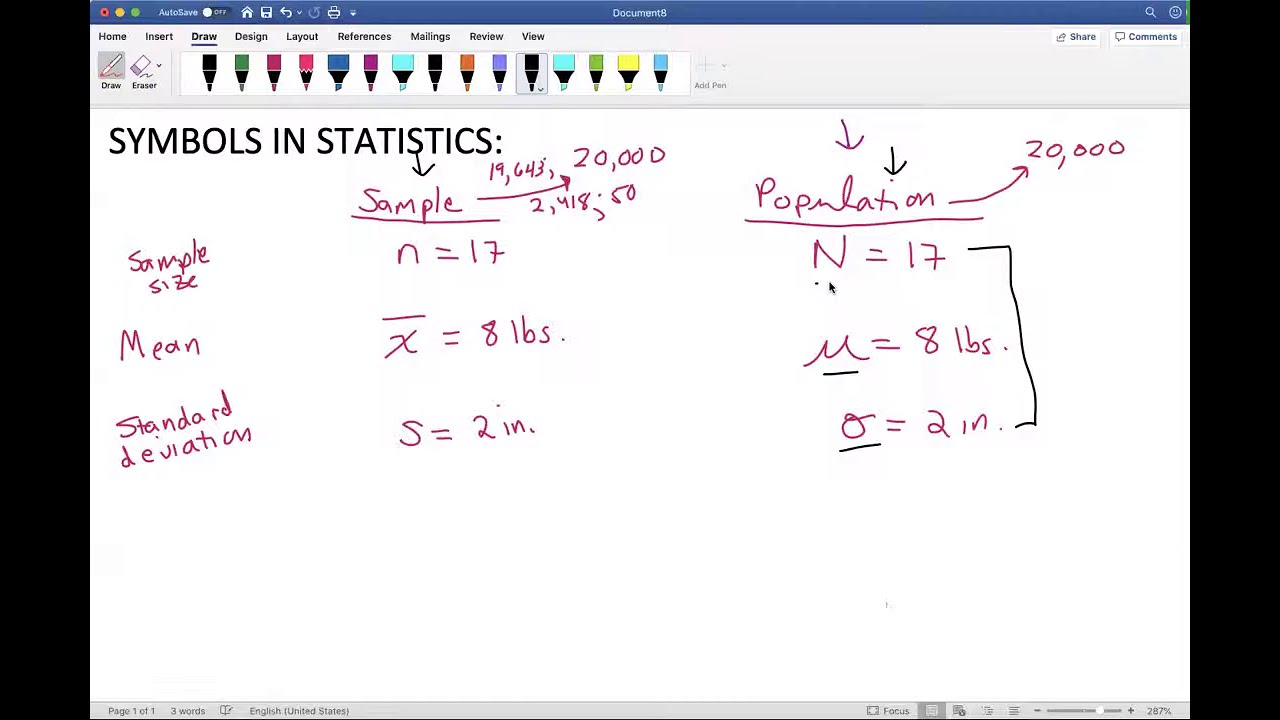
Symbols in statistics. Sample or Population?

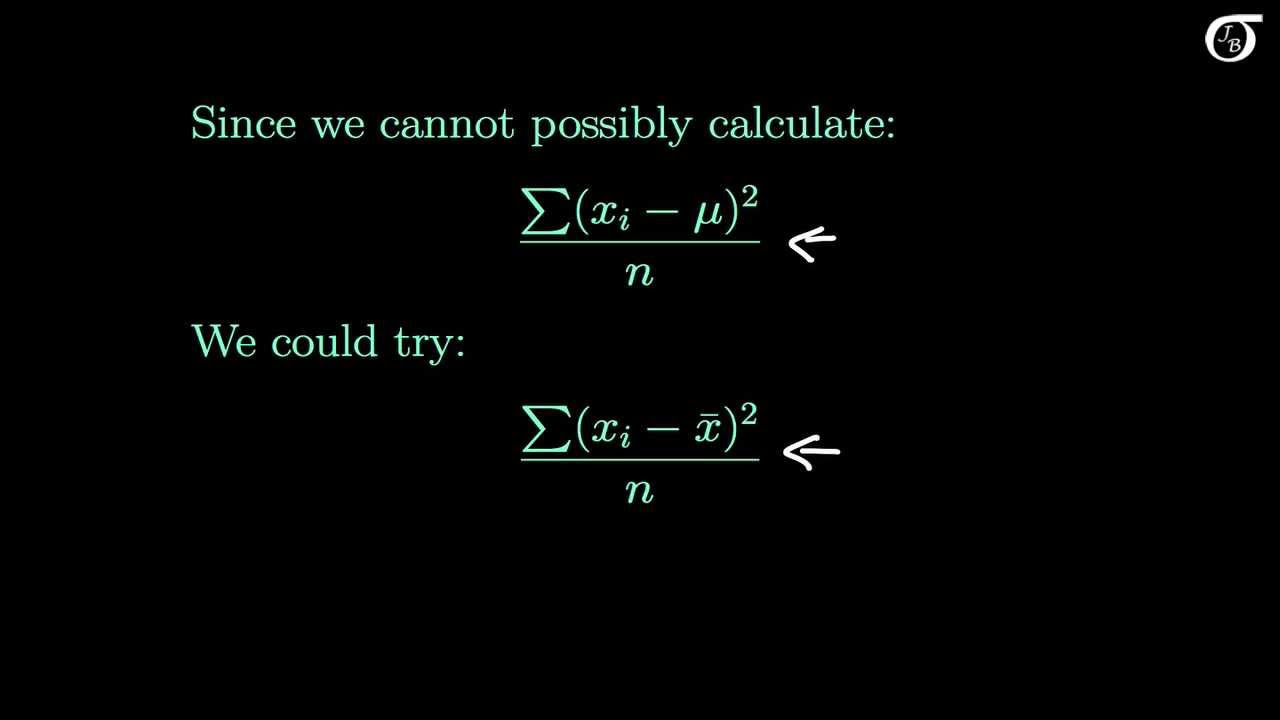
The Sample Variance: Why Divide by n-1?

Rate This

5.0 / 5 (0 votes)

Thanks for rating: