Solving a System Equations | #Algebra
TLDRThis educational video demonstrates the process of solving a unique system of equations involving two variables, x and y. The presenter begins by outlining the system and its restrictions, emphasizing that y cannot be zero due to its presence in the denominator. The solution method involves manipulating the equations to find conditions that lead to potential solutions. Through a step-by-step approach, the presenter eliminates impossible scenarios and arrives at a single valid solution: x = 1/2 and y = -1. Additionally, a second method is briefly discussed, involving algebraic manipulation to solve for y in terms of x. The video concludes with a visual representation of the solution using a graph, which confirms the intersection point of the equations at (1/2, -1). The presenter encourages engagement by asking viewers to comment, like, and subscribe for more content.
Takeaways
- 📚 The video is about solving a unique system of equations involving the variables x and y.
- 🔍 The system of equations is presented as \( x + y = xy \) and \( xy = \frac{x}{y} \), which are essentially the same.
- ❗ There is a restriction that y cannot equal zero because it is in the denominator.
- 🤔 The presenter starts by examining the equation \( \frac{xy}{x} = \frac{x}{y} \) and simplifies it to find conditions for x and y.
- 📉 From the simplification, it is deduced that either x is zero, y is one, or y is negative one.
- 🚫 The case where x equals zero is quickly dismissed because it leads to y also being zero, which is not allowed.
- 🔄 The case where y equals one leads to a contradiction, as it would imply \( x + 1 = x \), which is not possible.
- 🎯 The only valid solution from the initial analysis is when y equals negative one, leading to \( x = \frac{1}{2} \).
- 📈 An alternative method is discussed where the presenter solves for y in terms of x using the equation \( x + y = xy \).
- 🤓 The alternative method leads to a cubic equation, which after simplification and error correction, also results in \( x = \frac{1}{2} \) and \( y = -1 \).
- 📊 The video concludes with a graph in Desmos that visually confirms the single solution at \( (x, y) = (\frac{1}{2}, -1) \).
Q & A
What is the main topic of the video?
-The video is about solving a system of equations involving variables x and y.
What are the two equations presented in the video?
-The two equations are X + Y = XY and XY = X/Y.
What is the restriction mentioned for the variable y?
-The restriction is that y cannot equal zero because it is in the denominator of one of the equations.
What is the initial approach to solving the system of equations?
-The initial approach is to start with the equation XY = X/Y, factor out X, and find the possible values for x and y.
What are the possible values for x and y derived from the first approach?
-The possible values are x = 0, y = 1, or y = -1.
Why is x = 0 not a valid solution?
-x = 0 is not valid because it leads to y = 0, which contradicts the restriction that y cannot be zero.
What happens when y = 1 is considered in the equations?
-When y = 1 is considered, it leads to an absurd result where X + 1 = X, which is not possible.
What is the solution when y = -1?
-When y = -1, the solution is x = 1/2, which satisfies the given equations.
What is the alternative method mentioned in the video for solving the system?
-The alternative method involves solving for y in terms of x using the equation X + Y = XY and then substituting this expression into the other equation.
What mistake was made during the alternative method, and how was it corrected?
-The mistake was in the replacement of y with x/(x-1) in the equation XY = X/Y. It was corrected by properly substituting and simplifying to find the values of x and y.
What is the final solution to the system of equations?
-The final solution is x = 1/2 and y = -1.
How does the video demonstrate the solution graphically?
-The video uses a graphing tool like Desmos to plot the equations and visually identify the intersection point, which corresponds to the solution x = 1/2 and y = -1.
Outlines
🔍 Solving a System of Equations with Restrictions
This paragraph introduces the concept of solving a system of equations, highlighting that there are two main equations involved: X + Y = XY and XY = X/Y. The speaker emphasizes the need to consider restrictions, such as Y cannot be zero due to its presence in the denominator. The approach involves manipulating the equations to find conditions and then applying these to the system to find solutions. The speaker also hints at a graphical method to solve the system, which will be discussed later in the video.
📈 Analyzing the Equations and Finding Solutions
The speaker begins by analyzing the equations X Y / X = X/Y and X + Y = XY, aiming to find conditions that satisfy both. By rearranging terms and factoring, it is deduced that X can be zero, Y can be one, or Y can be negative one. These findings are then tested against the original equations. The first case, where X is zero, is quickly dismissed as it leads to an invalid solution where Y would also be zero. The second case, where Y equals one, is also discarded as it leads to an impossible condition. The third and final case, where Y equals negative one, results in a valid solution where X equals one half. The speaker concludes that there is only one solution to the system: (X, Y) = (1/2, -1).
🤔 Exploring an Alternative Method for Solution
The speaker proposes an alternative method to solve the system, starting with the equation X + Y = XY. By isolating Y, the equation is transformed into Y = X / (X - 1), with the caveat that X cannot be one. The speaker then attempts to substitute this expression for Y into the second equation, XY = X/Y, but realizes a mistake in the process. After correcting the error, the speaker simplifies the equation to X^3 = X(X^2 - 2X + 1), which further simplifies to 2X^2 - X = 0. Factoring out X, the possible solutions are X = 0 or X = 1/2. Since X = 0 leads to an invalid solution (Y = 0), the valid solution is X = 1/2, which corresponds to Y = -1. The speaker then moves on to discuss the graphical representation of the equations in Desmos, confirming the single intersection point at (1/2, -1).
Mindmap
Keywords
💡System of Equations
💡Solution Method
💡Graph
💡Restrictions
💡Quotient
💡Factoring
💡Case Analysis
💡Infinity
💡Cross Multiply
💡Cubic Equation
💡Desmos
Highlights
Introduction to solving a system of equations with two equations: X + Y = XY and X + Y = X/Y.
Explanation of the restrictions, specifically that y cannot equal zero due to being in the denominator.
The interesting mathematical concept that two numbers whose quotient equals their product.
Method to solve the equations by putting everything on the same side and solving for x.
Factoring out x to simplify the equation and find possible values for x and y.
Finding that x can be zero, y can be one, or y can be negative one.
Elimination of the first case where x equals zero because it leads to y equals zero, which is not allowed.
Analysis of the second case where y equals one, leading to an impossibility.
Third case analysis with y equals negative one, resulting in a potential solution.
Solving for x when y equals negative one, finding x equals one half.
Conclusion that there is only one solution: x = 1/2, y = -1.
Introduction of an alternative second method to solve the system of equations.
Isolating y in terms of x by solving X + Y = XY for y.
Explanation of why x cannot equal one based on the derived equation for y.
Mistake identification and correction in the process of solving the equations.
Final solution confirmation with x = 1/2 and y = -1 using the alternative method.
Graphing the equations in Desmos to visually confirm the single intersection point.
Conclusion and call to action for viewers to comment, like, and subscribe.
Transcripts
Browse More Related Video
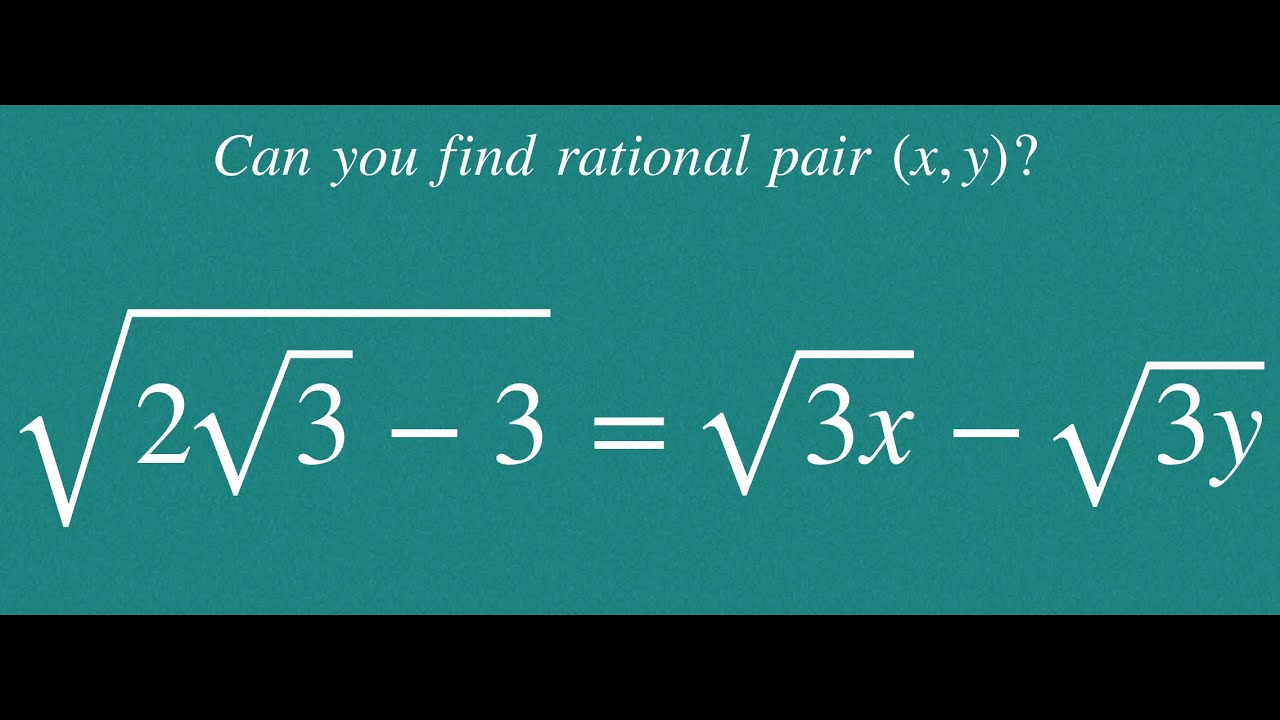
Radical equation | Radical simplification | math tricks |Math Olympiad | unique math tricks
Solving 3 Equations with 3 Unknowns

Solving 3 Equations for 3 Unknowns Using a Matrix in Row Echelon Form

Lagrange Multiplier Example
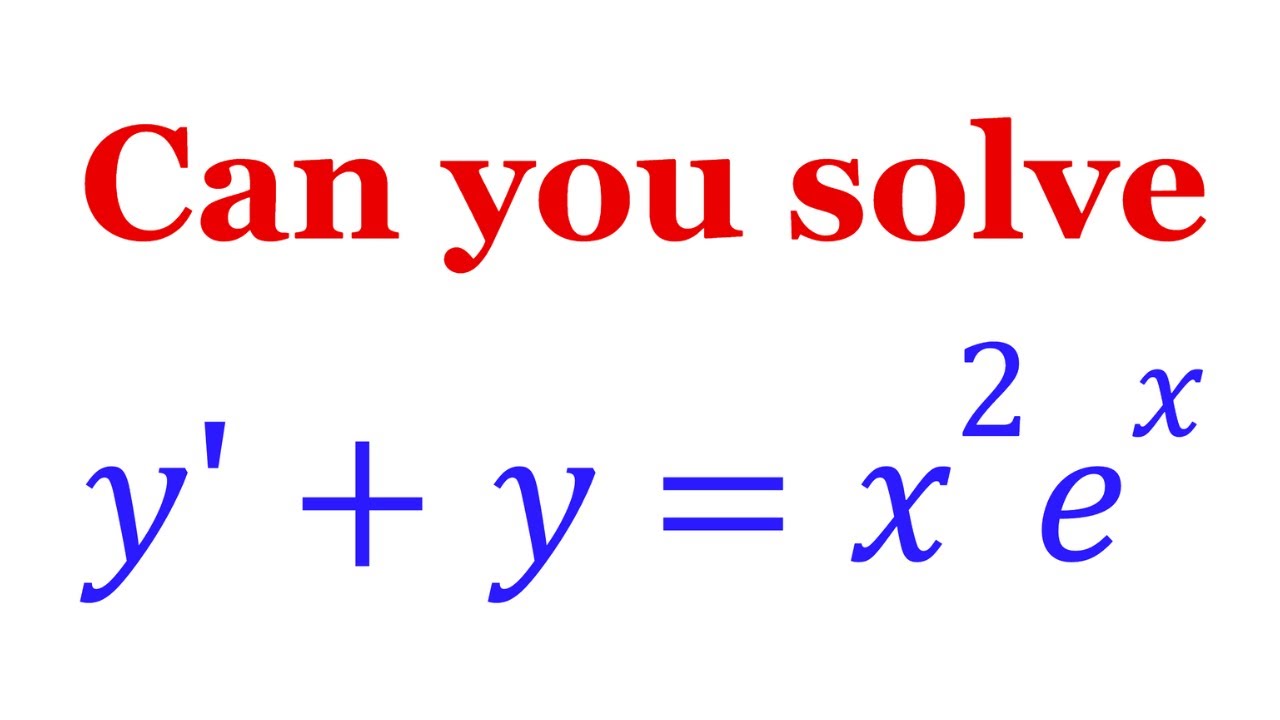
Let's Solve An Interesting Differential Equation
Solving Systems of Equations By Graphing
5.0 / 5 (0 votes)
Thanks for rating: